1.6 Связь между статистическим распределением выборки и изучаемым распределением вероятностей

Получив выборку и описав ее, мы хотим это описание распространить на всю генеральную совокупность. А генеральная совокупность – это некоторое распределение вероятностей. И наша задача заключается в том, чтобы по полученному экспериментальному материалу сделать выводы о виде распределения или, если есть какие-то теоретические предпосылки о виде распределения, получить оценки значений его числовых параметров – например, если выборка сделана из нормального распределения, оценить с помощью выборки его параметры, или оценить с помощью выборки параметр пуассоновского распределения. Для того, чтобы понять, что нам дает выборка для решения этой задачи, представим себе урну, в которой лежат n шаров. На m₁ из них написано число х₁, на m₂ шарах написано число х₂ и т.д., на m_k шарах – число х_k. Эта урна и есть наша выборка. Согласно классическому определению вероятностей можно говорить о распределении вероятностей этой урны – вероятность достать из нее число x_i равна m_i/n. Заметим, что таблица статистического распределения выборки описывает закон распределения дискретной случайной величины, для которого возможные значения случайной величины – варианты выборки x_i, а соответствующие им вероятности – их относительные частоты m_i/n.

Следовательно, таблица статистического распределения выборки – это таблица распределения выборки, построенного по классической схеме. Эти соображения и послужили основанием для того, чтобы построенную по выборке таблицу значений и их относительных частот - назвать таблицей статистического распределения выборки.

Обозначим:

В силу того, что 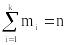, выполняется и:

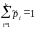
(при округлении этих значений, неизбежном при переводе их в десятичную дробь, следует побеспокоиться, чтобы это правило выполнялось и после округления). В этих обозначениях таблица статистического распределения выборки имеет вид (таблица 1.10):

Таблица 1.10. Эмпирическое распределение (распределение выборки)

Значения xi	x1	x2	…	xk
Частоты			…

1.6.1 Полигон и многоугольник распределения

Если наблюдения производятся над дискретной случайной величиной, то у каждого значения x_i есть теоретическая вероятность его появления в процессе наблюдения. Обозначим ее через p_i. Это означает, что в нашем эксперименте исследуется дискретное распределение, таблица распре-деления которого имеет вид (таблица 1.11):

Таблица 1.11. Генеральное распределение

Значения xi	x1	x2	…	xk
Частоты pi	р1	р2	…	рk

Таким образом, мы хотим вместо распределения, задаваемого таблицей 1.7, на практике пользоваться распределением, задаваемым таблицей 1.6. Так что встает вопрос об оценке близости этих распределений.

Значение является выборочным аналогом (он вычисляется по выборке) вероятности p_i появления значения x_i. В силу теоремы Бернулли, вычисляемая по выборке относительная частота обладает свойством статистической устойчивости и стремится по вероятности к вероятности p_i. Поясним коротко, что означает термин “сходится по вероятности”. В курсе анализа изучается понятие сходимости. Последовательность {a_n} называется сходящейся к a при n, стремящемся к бесконечности, если за счет роста n можно добиться, чтобы разность |a_n – a| стала как угодно мала. Сходимость случайной величины по вероятности к некоторому значению означает, что, несмотря на увеличение числа испытаний n, могут встретиться значения случайной величины, довольно сильно отличающиеся от предельного значения, но процент таких испытаний будет с ростом n уменьшаться (вероятность отклонения от предела стремится к 0). Сходимость по вероятности к p_i означает, что для любого  > 0, несмотря на рост n, будут встречаться выборки, для которых нарушается соотношение , но с ростом числа испытаний n вероятность (доля или процент таких выборок среди множества всех возможных выборок) стремится к нулю.

Полигон, построенный по относительным частотам, – это просто статистический (эмпири-ческий) многоугольник генерального распределения. В силу теоремы Бернулли при n, стремящем-ся к бесконечности, он сходится по вероятности к многоугольнику генерального распределения.