1.2 Методы отбора. Репрезентативность выборки. Выборка повторная и бесповторная

Выборочный метод исследования является единственно возможным в случае бесконечной генеральной совокупности или в случае, когда исследование связано с уничтожением наблюда-емых объектов. Кроме того, он позволяет существенно экономить затраты ресурсов. Недостатком его является появление ошибок исследования, (их называют ошибками репрезентативности), которые связаны с тем, что изучается только часть объекта. Математическая статистика дает рекомендации, как организовать исследование, чтобы свести эти ошибки к минимуму, и дает методику оценки этих ошибок.

Чтобы иметь возможность по данным выборки судить о генеральной совокупности, выборка должна быть отобрана так, чтобы она давала правильное представление о генеральной сово-купности.

Пример 1.2. Для проверки качества продукции отобрана партия втулок, изготовленная случайно выбранным рабочим. Но в цехе по производству втулок работают квалифицированные токари и начинающие. Ясно, что если эти втулки изготовлены квалифицированным токарем, то представление о качестве продукции, выпускаемой всем цехом, будет “завышенным”, а если изучать втулки, изготовленные начинающим токарем, то “заниженным”.

Для того, чтобы выборка давала представление о генеральной совокупности, необходимо, чтобы соблюдался принцип равной возможности для всех элементов генеральной совокупности - быть отобранными в выборку. В приведенном примере в выборку попали втулки, изготовленные только одним рабочим, т.е. эти втулки, при отборе, имели преимущество и указанный принцип соблюден не был.

Выборка называется репрезентативной (представительной – от англ. representative), если она достаточно хорошо воспроизводит генеральную совокупность, т.е. это выборка, которая производится так, что все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.

Обеспечить это условие можно различными средствами. Например, отбор можно производить просто на основе таблиц случайных чисел. Таких таблиц сейчас издано много; разработаны программы для ЭВМ – генераторы случайных чисел. Если изучается объект, состоящий из многих разнородных частей, например, мнение избирателей, надо позаботиться о том, чтобы в выборке в соответствующей пропорции были представлены все части системы. В ней должны быть представлены горожане и сельские жители, молодежь и пенсионеры, военные, рабочие, интеллигенция и т.д. из всех частей страны и в той же пропорции, что и во всей стране.

К чему может привести несоблюдение этого правила показывают многочисленные случаи несбывшихся предвыборных прогнозов. Например, в 1936 году перед президентскими выборами в США журнал “Literary Digest” провел опрос 10 миллионов избирателей и предсказал, что Франклин Рузвельт проиграет выборы. Фамилии избирателей были взяты из телефонных книг. Но в 1930-е годы во время депрессии люди, имевшие телефон, не представляли всех избирателей США, выборка оказалась не репрезентативной и прогноз не оправдался. На телевидении вошло в моду проводить экспресс-опросы во время передачи – желающие сообщить свое мнение могут позвонить в студию и ответить на вопрос “да”, “нет” или “не знаю”. Такая форма опроса не дает репрезентативной выборки. Примером организации репрезентативного опроса может служить, в частности, метод отбора, который был применен в Англии при проведении обследования рациона питания среднего англичанина. Выборка извлекалась методом трехступенчатого отбора. На первом этапе было отобрано 50 избирательных округов. Затем из них было отобрано некоторое количество избирательных участков. На третьем – некоторое количество семей внутри этих участков. На каждом этапе отбор был строго случайным.

Существуют специальные приёмы отбора, обеспечивающие репрезентативность выборки.

Опишем простейшую схему получения репрезентативной выборки из конечной, не очень большой генеральной совокупности.

Все объекты генеральной совокупности нумеруют, номера записывают на отдельные карточки, карточки перемешивают и выбирают одну наудачу. Объект, номер которого совпал с номером на карточке, считается попавшим в выборку. Операцию повторяют до тех пор, пока не наберется нужный объем выборки. При этом, если случайно отобранная карточка возвращается обратно в общую совокупность и, следовательно, раз отобранный в выборку объект может быть отобран повторно, то имеет место выборка повторная, или выборка с возвратом, а если отобранная карточка и, следовательно, отобранный в выборку объект назад не возвращается, то осуществляется выборка бесповторная или выборка без возврата. Вместо перемешивания карточек, можно использовать таблицы случайных чисел. Их можно найти в большинстве книг по статистике. Следует заметить, что если в выборке с возвратом испытания независимы, то в выборке без возврата испытания уже зависимы. Для демонстрации разницы между этими схемами рассмотрим простейший пример.

Пример 1.3. В урне n белых и m черных шаров. Наугад вынимаем два шара. А₁ – событие, состоящее в том, что первый шар белый, А₂ – второй шар тоже белый.

Выборка с возвратом:

Р(А₁) = Р(А₂) = n/(n+m), Р(А₂/А₁) = Р(А₂) = n/(n+m).

Выборка без возврата:

Р(А₁) = n/(n+m).

Для того, чтобы найти вероятность Р(А₂), определим событие В₁ – первый вынутый шар – черный и воспользуемся формулой полной вероятности:

.

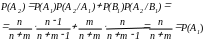Заметим, что

.

Таким образом, для выборки с возвратом вероятность во втором испытании вытащить белый шар такая же, как и в первом испытании: условная вероятность совпадает с безусловной, следовательно, испытания независимы. Для выборки без возврата вероятность во втором испытании вытащить белый шар такая же, как и в первом испытании, но независимости испытаний уже нет. Легко видеть, что если n и m велики, то зависимость испытаний является слабой. Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выбор-ками стирается.

В дальнейшем будем предполагать, что требование репрезентативности выборки выполнено, испытания независимы и будем обсуждать только вопросы обработки выборочных данных.