4.5 Нормировка

Если то ; .

Математическая статистика

5.1 Выборка

.

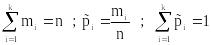Для дискретного вариационного ряда медиана d:

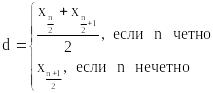
Размах вариационного ряда – расстояние x_max – x_min между крайними членами вариационного ряда

Группировка состоит в том, что область на оси x, куда попали значения x₁,x₂,...,x_n, разбивают на интервалы I₁,I₂,...,I_k и подсчитывают частоту попадания значений величины в каждый интервал. Самый простой способ группировки – округление данных.

Согласно формуле Серджеса рекомендуемое число интервалов:

k = 1 + 3,322lgn,

а величину интервала h можно вычислить по формуле:

,

где x_max – x_min разность между наибольшим и наименьшим значением в выборке (ее размах).

За начало первого интервала рекомендуется брать величину:

х_нач = x_min – 0,5h.

Кроме того, необходимо следить, чтобы не было интервалов, в которые попало меньше пяти значений.

5.2 Теоретические и эмпирические моменты

Начальный момент l-го порядка a_l:

для дискретного распределения и

для непрерывного распределения.

l-ый центральный момент b_l:

для дискретного распределения и

для непрерывного распределения,

где = а₁ – математическое ожидание распределения

Вариационный ряд без повторов

l-ый начальный эмпирический момент:

.

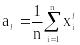l-ый центральный эмпирический момент:

_.

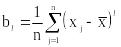Вариационный ряд, заданный таблицей:

.

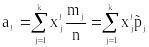
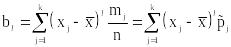5.3 Выборочное (эмпирическое) среднее

Выборка задана вариационным рядом: .

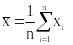Выборка задана таблицей:

.

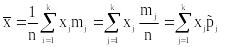Свойства те же, что у математического ожидания.

Распределение выборочного среднего:

.

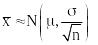4 Выборочная (эмпирическая) дисперсия s2

Выборка задана вариационным рядом:

.

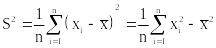Выборка задана таблицей:

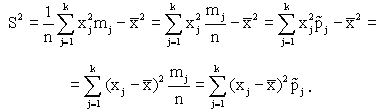
Свойства те же, что у дисперсии.

Исправленная, несмещенная оценка для дисперсии:

.

5.5 Доверительные интервалы

Доверительный интервал с уровнем доверия  для математического ожидания а нормального распределения для случая, когда известно среднеквадратическое отклонение распределения :

Двусторонний: (таблица  в 1-м столбце)

односторонний: (таблица 5  = 1– в 3-м столбце)

и (Таблица 5  = 1– в 3-м столбце)

Доверительный интервал с уровнем доверия  для математического ожидания  нор-мального распределения для случая, когда среднеквадратическое отклонение распределения  неизвестно:

Двусторонний:

или

,

где S – корень из эмпирической дисперсии, а s – корень из исправленной эмпирической дисперсии (таблица 6  в верхней строке)

Односторонние: (таблица 6  в нижней строке) и (таблица 6  в нижней строке).

В этих формулах s² несмещенная оценка для дисперсии:

.

5.6 Оценка требуемого объема выборки

Минимальный объем выборки n, обеспечивающий чтобы точность оценки, полученной по ней для а с надежностью , не превосходила заданного значения  (то есть ), когда средне-квадратическое отклонение известно, задается формулой:

.

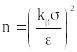7 Доверительный интервал для вероятности успеха в схеме Бернулли

Основная формула – следствие интегральной теоремы Муавра-Лапласа, из которой выводятся любые соотношения между эмпирической частотой, генеральной частотой, n и вероятностью :

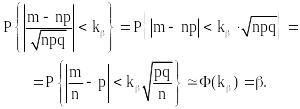
Отсюда формула доверительного интервала для выборки с возвратом:

, где .

Для выборки без возврата формулу надо подправить:

Объем выборки n, обеспечивающий, чтобы точность оценки, полученной по ней для р с надежностью , не превосходила заданного значения , т.е. , находится по формуле:

.