5.4 Проверка гипотез методом последовательного анализа

Когда проведение каждого испытания стоит очень дорого, для того чтобы при проверке статистических гипотез минимизировать число испытаний, рекомендуется применять последова-тельные критерии.

Последовательные критерии впервые были предложены А. Вальдом в 1946 г. Как уже было сказано, при применении этого метода (последовательного анализа) необходимое число наблюдений не фиксируется заранее, как мы это делали, например, в только что рассмотренной задаче, а определяется в процессе эксперимента; область значений в n-мерном пространстве делится на три части: критическую для гипотезы Н₀ (ее вероятность при условии, что верна гипотеза Н₀ – a), критическую для гипотезы Н₁ (ее вероятность при условии, что верна гипотеза Н₁ – b) и область неопределенности. Эксперимент продолжается, пока выборочные значения не попадут в одну из критических областей – или критическую для гипотезы Н₀, или критическую для гипотезы Н₁.

В самом общем виде по этому методу последовательность наблюдений проводится по следу-ющей схеме.

1. Вычисляются границы критерия:

А = (1–)/a, B = /(1–a),

где a – вероятность отклонить основную гипотезу, когда она верна,

 – вероятность принять основную гипотезу, когда она неверна.

2. На каждом шаге вычисляется отношение вероятностей L_m:

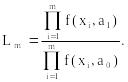
В этом отношении а₀ – значение параметра для основной гипотезы, а₁ – для альтернативной, m – текущее число наблюдений или номер шага, f(x, ) – плотность вероятности для непрерывной модели и вероятность принять значение х для дискретной модели. Обычно удобнее вычислять ln L_m.

3. Если ln L_m ln B, то принимается основная гипотеза.

Если ln L_m ln A, то основная гипотеза отклоняется. Если не выполняется ни одно из неравенств, эксперимент продолжается.

Доказана теорема о том, что с вероятностью 1 эта процедура заканчивается за конечное число шагов.

Организация эксперимента по методу последовательного статистического анализа позво-ляет уменьшить число испытаний n в среднем вдвое (а при a =  даже в 4 раза) по сравнению с оптимальным методом с фиксированным числом наблюдений.

Пример 5.4. Рассмотрим применение последовательного анализа в условиях предыдущей задачи, когда с помощью эксперимента мы хотим решить вопрос о среднем значении нормального распределения, имеющего среднеквадратическое отклонение , когда заданы ошибки 1-го и 2-го рода и . Процедура последовательного анализа будет выглядеть следующим образом.

Вычислим А = (1–)/ и B = /(1–). На каждом шаге эксперимента вычисляется значение lnL_m.

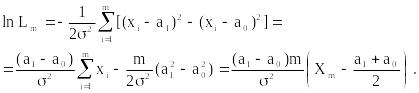
Решение о гипотезе принимается в соответствии с пунктом 3 решающего правила:

– принимается Н₀.

– принимается Н₁.

Эксперимент продолжается, если:

Для упрощения расчетов рассмотрим случай:

Н₀ отклоняется, если

Н₁ принимается, если

Эксперимент продолжается, если:

Так как , то при n = 16 (см. выше), если эксперимент еще не закончится, можно воспользоваться критерием, предлагаемым методом с фиксированным числом наблюдений:

Если X_m > 1/2(a₀+a₁) – Н₀ отклоняется.

Если X_m < 1/2(a₀+a₁) – Н₀ принимается.

Схематически для a =  это можно изобразить следующим образом (рисунок 5.2):

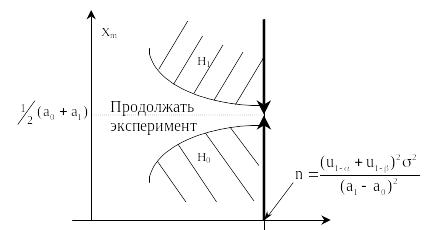
Рисунок 5.2

ПРИЛОЖЕНИЕ 1 Греческий алфавит

ПРИЛОЖЕНИЕ 2 Теория вероятностей

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

1 Функция распределения F(x), плотность f(x) и их свойства

.

;

;

;

;

;

.

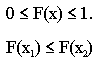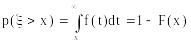2 Математическое ожидание и его свойства

Для дискретного распределения:

.

Для непрерывного распределения:

;

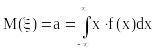M(С) = С;

;

;

.

3 Дисперсия, среднеквадратическое отклонение и их свойства

(дискретный случай),

(непрерывный случай).

D(C) = 0;

.

Для независимых x_i:

;

;

;

.

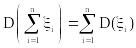4 Примеры распределений и значения их числовых характеристик

4.1 Испытание с двумя исходами, биномиальное распределение

Пусть в результате испытания с вероятностью р происходит событие (случайная величина  – индикатор наступления А приняла значение 1), а с вероятностью q = 1–р противоположное ему событие ( приняла значение 0). Это распределение задают таблицей:

xi	0	1
pi	q	p

M() = 0q + 1p = p

D() = 0q + 1²p – p² = p(1–p) = pq

Вероятность, что число успехов , полученных при n независимых испытаниях, проводящихся над такой случайной величиной (схема Бернулли), примет значение m, задается формулой Бернулли:

4.2 Распределение Пуассона

Случайная величина, которая принимает значение m с вероятностью

,

где m=0,1,2,…, а  – положительная постоянная величина, называется распределенной по Пуассону с параметром 

4.3 Равномерное распределение

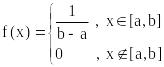
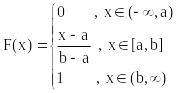
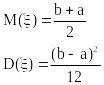
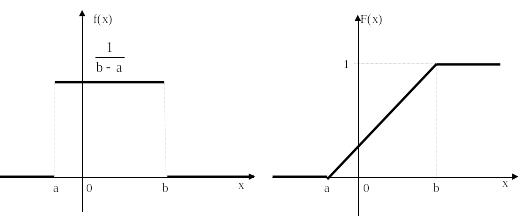
Рисунок 6.1

4.4 Показательное распределение

Непрерывная случайная величина имеет показательное распределение, если её плотность вероятности имеет вид

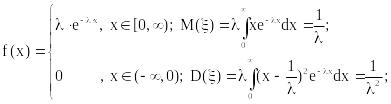
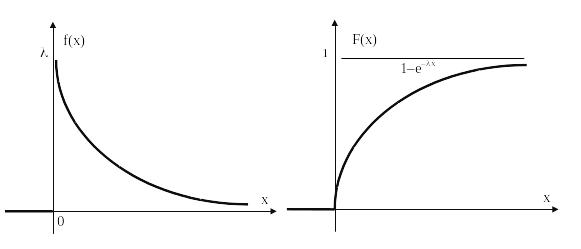
Рисунок 6.2

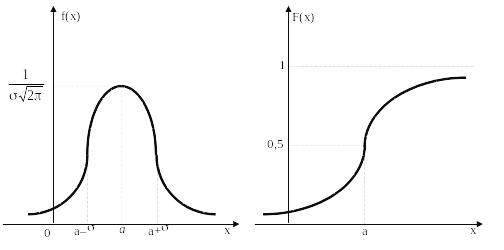
4.5 Нормальное распределение

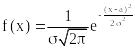
Параметрами, определяющими нормальное распределение N(a,) являются a – математическое ожидание и  – среднеквадратическое отклонение.

~N(0,1) называют стандартной нормальной. Ее плотность вероятности и функция распределения задаются формулами:

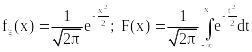
– таблица 3 приложения 3.

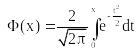
– функция Лапласа (Таблица 4)

Функция распределения стандартного нормального закона F(x) связана с функцией Лапласа Ф(х) соотношением:

Для ~N(0,1):

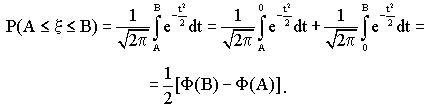
Для ~N(a,):

правило трёх :

_,

правило двух :

_,

р{|–a| < k_} = (k_) = .

Вероятности попадания в полуинтервал для ~N(a,):

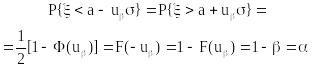
В частности: