5 Методы, основанные на свойствах функции правдоподобия

5.1 Функция правдоподобия

Функцией правдоподобия называется плотность вероятности (в дискретной модели просто вероятность) совместного появления результатов выборки x₁, x₂,…,x_n.

Таким образом, для распределения, зависящего от параметра  функция правдоподобия L(x₁,x₂,…x_n,) задается по формуле:

,

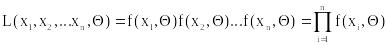где f(x,) – плотность распределения в случае непрерывной модели и вероятность значения х в дискретной модели.

5.2 Метод максимального правдоподобия для получения оценки неизвестного параметра 

Р. Фишером для получения оценки неизвестного параметра  был в 1912 г. предложен метод, обладающий оптимальными свойствами, который называется методом максимального правдоподобия.

Согласно методу максимального правдоподобия в качестве оценки неизвестного параметра  принимается такое значение _n, при котором плотность вероятности (в дискретной модели просто вероятность) совместного появления результатов выборки x₁, x₂,…x_n. максимальна, и, следовательно, функция правдоподобия достигает максимума.

В точке, в которой значение функции L максимально, ее производная по параметру  обращается в ноль. Чаще всего ищется не максимум функции L, а максимум ее логарифма, так как максимум этих функций достигается при одном и том же значении . Следовательно, для нахож-дения оценки требуется решить уравнение (или, если параметров несколько, систему уравнений) правдоподобия:

или .

Основной недостаток метода максимального правдоподобия – трудность вычисления оценок, связанных с решением уравнения правдоподобия. Кроме того, необходимо знать тип анализи-руемого закона распределения f(х,), что во многих случаях оказывается практически нереальным. Достоинством метода является то, что при достаточно общих условиях оценки максимального правдоподобия являются состоятельными, асимптотически эффективными и имеют асимптоти-чески нормальное распределение.

Пример 5.1. Методом максимального правдоподобия найти оценку для вероятности р наступления события А в схеме Бернулли (n раз проводятся независимые испытания, при которых возможны только два исхода – с вероятностью р происходит событие А, с вероятностью q = 1–p событие А не происходит). В результате n испытаний событие А произошло m раз.

Выписываем функцию правдоподобия:

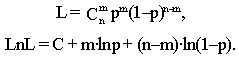
Откуда

.

Таким образом, оценкой метода максимального правдоподобия вероятности р события А является относительная частота m/n этого события.

Пример 5.2. Выборка производится из нормального распределения N(a).

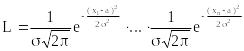
Следовательно, ln L равен

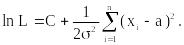
Приравняв нулю производные по а и по , можно показать, что для его параметров а и ² оценками наибольшего правдоподобия будут те же и S², которые мы получили в качестве оценок для этих параметров методом моментов.

5.3 Функции правдоподобия в задачах проверки гипотез

Рассмотрим простейшую задачу проверки гипотезы, когда конкурирующими являются две простые гипотезы: Н₀ – значение неизвестного параметра распределения равно а₀, и альтерна-тивная ей Н₁ – значение неизвестного параметра распределения равно а₁. На основе статисти-ческого эксперимента надо принять решение о том, какая из гипотез правильная.

Составим отношение вероятностей L_n (отношение функций правдоподобия для конкури-рующих гипотез) для n испытаний:

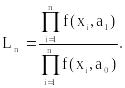
Задачу о конкурирующих гипотезах можно решать, изучая поведение отношения вероят-ностей. Согласно теореме Неймана-Пирсона, там, где оно больше некоторого порога (L_n > C или lnL_n > lnC), следует предпочесть гипотезу Н₁, в противном случае – Н₀. Порог C надо принять таким, чтобы обеспечить уверенность в том, что, если верна гипотеза Н₀, то мы ее отбросим с вероятностью не большей, чем . Симметричным рассуждением (поменяв местами гипотезы), находим порог для значений отношения вероятностей такой, что если верна гипотеза Н₁, то ее мы отбросим с вероятностью, не большей чем .

Пример 5.3. Производятся испытания с величиной x, которая распределена нормально с известной дисперсией s². Относительно математического ожидания а имеются две гипотезы: Н₀ состоит в том, что а = а₀, и Н₁ – состоит в том, что а=а₁. Вычислим lnL_n.

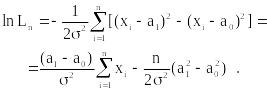
Таким образом, вместо порога функции правдоподобия, обеспечивающего ошибку a, можно искать порог для статистики . Порог ищется по распределению вероятностей. Эта статистика имеет нормальное распределение. Тем же способом найдем и порог, обеспечивающий требуемую величину ошибки 2-го рода. Если верна гипотеза

Задача свелась к рассмотренному выше примеру. Надо вычислить необходимое число испы-таний n по формуле:

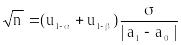
и пороговое соотношение для X_n из уравнения:

,

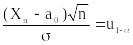с учетом вычисленного значения n. Это дает:

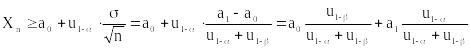
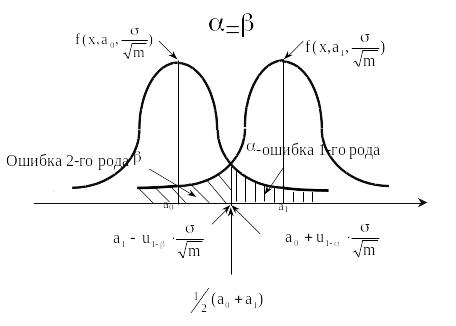
Рисунок 5.1

Таким образом, в терминах отношения правдоподобия процедура проверки гипотезы о среднем, когда конкурируют две простые гипотезы для значений среднего а₀ и а₁ при генеральном среднеквадратическом отклонении  для заданных ошибок 1-го и 2-го рода a и , выглядит следующим образом:

1. Вычисляется число испытаний n по формуле:

2. Для величины X_n вычисляется порог, определяющий критическую область критерия. Критическая область, при попадании в которую гипотеза Н₀ отвергается, имеет вид:

^.

На рисунок 5.1 изображены плотности распределения статистики X_n и критические области для случая a = . При a =  критерий выглядит очень просто. Число испытаний находится по формуле:

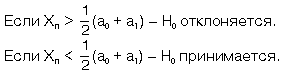
(Какая плотность больше, та и считается верной).