4.2 Сравнение двух генеральных средних

Рассмотрим две независимые выборки x₁,x₂,...,x_n и y₁,y₂,...,y_n, извлеченные из нормальных генеральных совокупностей с одинаковыми дисперсиями , причем объемы выборок соответственно n и m, а средние и дисперсия неизвестны. Требуется проверить гипотезу о том, что . Альтернативной является гипотеза .

Как известно, выборочные средние – нормально (или приблизительно - нормально) распреде-ленные величины, следовательно, их разность – нормальная величина со средним и дисперсией, которая вычисляется по формуле:

Если бы дисперсия была известна, мы могли бы для проверки гипотезы воспользоваться свойствами и таблицами нормального распределения, как мы это делали при построении довери-тельного интервала для среднего при известной дисперсии. В силу того, что неизвестна, заменим в наших рассуждениях неизвестную дисперсию на ее эмпирический аналог.

Итак, для проверки гипотезы построим статистику:

,

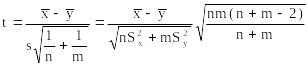где

Теперь к статистике t применим те же рассуждения, которые мы применяли к статистике Т.

Если гипотеза верна, статистика t имеет распределение Стьюдента с n+m–2 степенями свободы и в качестве области _ можно взять интервал, симметричный относительно 0, в который величина x, распределенная по Стьюденту, попадает с вероятностью , т.е.

_ = [–t_n+m–2;+t_n+m–2;], где P(|| < t_n+m–2;) = .

Таким образом, если нам заданы две выборки и уровень значимости , мы вычисляем значение статистики t и ищем по , n и m в таблице 6 (в ней содержатся критические значения распределения Стьюдента) значение t_n+m–2;a. Если выполняется

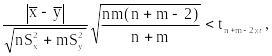
то мы принимаем гипотезу о том что . И отвергаем гипотезу , если это неравенство не выполняется, так как произошло событие из дополнительной области, вероятность которой . На рисунке 4.1 заштрихованная площадь (вероятность попасть в область) равна

,

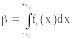на рисунке 4.2 заштрихована площадь  = 1– области, где гипотеза не принимается.

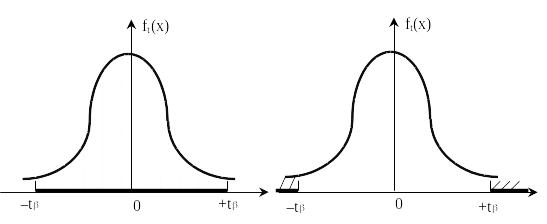
Рисунок 4.1 Рисунок 4.2

Если оказалось, что , можно проверять гипотезу о том, что , когда альтернативной гипотезой является _. В этом случае строится “односторонняя” область, попадание в которую дает основание принять основную гипотезу. А именно, в таблице 6 в нижней строке отыскивается  = 1 – , где – заданный уровень доверия, в строке с нужным числом степеней свободы находим границу интервала t_n+m–2;a. Далее, если выполняется:

то первая гипотеза неверна и принимается, что .

Можно проверять гипотезу о том, что , когда альтернативной гипотезой является . В этом случае также строится “односторонняя” область, попадание в которую дает основание принять первую гипотезу (рисунок 4.3). А именно, гипотеза о том, что не принимается, а принимается гипотеза тогда, когда

C помощью нижней строки таблица 6 распределения Стьюдента (см. приложение 3) мы решали уравнения:

P{ < –t_n+m–2;a} = a, и P{> t_n+m–2;a} = a,

где – уровень значимости.

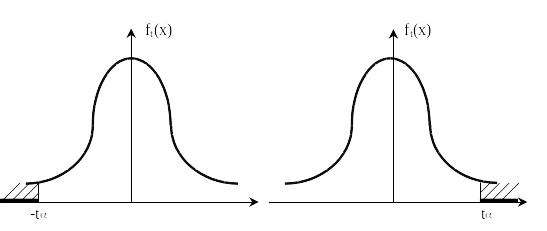
Рисунок 4.3

Замечание. Было бы корректно сначала проверить гипотезу о равенстве дисперсий с помощью их выборочных оценок. Во второй части нашего руководства мы научимся делать такую проверку. Использовать значение статистики Т можно только, если прошла гипотеза о равенстве дисперсий. Если дисперсии и неизвестны и не предполагается, что они равны, статистика Т также имеет распределение Стьюдента. Но соответствующее ему число степеней свободы опреде-ляется приближенно и более сложным образом.

Итак, перечислим критерии, по которым проверяется статистическая гипотеза о том, что средние значения двух генеральных совокупностей, имеющих одинаковые дисперсии, совпадают _x_y на уровне значимости . Они выведены из формул для двустороннего и одностороннего доверительного интервала для уровня доверия  = 1–.

Вычисляем по выборке значение статистики t:

,

где

.

1. Критическая область для односторонней проверки гипотезы, что средние значения двух генеральных совокупностей совпадают ( ) по сравнению с альтернативой на уровне значимости  определяется неравенством:

|t| > t_n–1;

(t_n–1;a отыскивается по таблице 6 критических значений распределения Стьюдента,  в нижней строке).

2. Критическая область для односторонней проверки гипотезы, что средние значения двух генеральных совокупностей совпадают ( ) по сравнению с альтернативой на уровне значимости  определяется неравенством:

t > t_n–1;a

(t_n–1;a отыскивается по таблице 6 критических значений распределения Стьюдента, a в нижней строке).

Если вычисленное значение статистики t попадает в критическую область, то основная гипотеза отвергается. Вероятность попадания в эту область равна принятому уровню значимости . В этом случае принимается альтернативная гипотеза.

Пример 4.2. Результаты исследования двух сортов резины на покрышках (в баллах) приведены в таблице:

Номер покрышки	1	2	3	4
Износ для сорта А	32	40	36	35
Износ для сорта В	25	28	27	26

Сделать проверку гипотезы о том, что резина сорта А больше изнашивается, чем резина сорта В.

Решение.

,

.

.

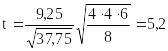Статистика распределена по Стьюденту с шестью степенями свободы. Значение t = 5,2 вы-ходит далеко за пределы интервала, имеющего уровень доверия 0,99 (этот интервал (–3,14; 3,14)). Следовательно, гипотеза о том, что оба сорта резины изнашиваются одинаково, не проходит. А проходит альтернативная ей “односторонняя” гипотеза о том, что резина сорта А изнашивается сильнее.

Заметим, что сделанный вывод “заметен на глаз” и без расчетов. Такой результат получится во всех случаях, когда вычисленное по испытаниям значение статистики t > 4. При близости значения t к числам 2 или 3 вывод может включать в себя уровень доверия к нему как параметр (вспомните правила двух и трех ). Если уровень доверия, с которым сделан вывод, не устраивает, надо позаботиться об улучшении опыта, например, увеличить число испытаний. Покажем это на примере.

Пример 4.3. Сравниваются две марки бензина А и В. На 11 машинах одинаковой мощности при разовом пробеге по кольцевому шоссе испытан бензин марок А и В. При испытании бензина марки В одна машина в пути вышла из строя и для нее данные по бензину отсутствуют. Расход бензина в пересчете на 100 км пути задан таблицей:

I	1	2	3	4	5	6	7	8	9	10	11
xi	10,51	11,86	10,5	9,1	9,21	10,74	10,75	10,8	11,3	11,8	10,9	N=11
yi	13,23	13,0	11,5	10,4	11,8	11,6	10,64	12,3	11,1	11,6	–	m=10

Дисперсия расхода марок бензина А и В неизвестна и предполагается одинаковой. Можно ли с уровнем доверия 0,95 принять, что истинные средние расходы этих видов бензина одинаковы?

1. Вычисляем по выборкам:

^{, ,}

,

.

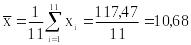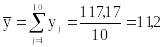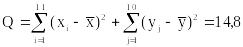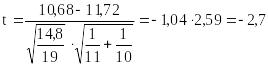2. Находим из таблицы 6 критических значений распределения Стьюдента t_19;0,95 = 2,1.

3. Так как |t| < t_19;0,95 не выполняется, гипотезу о том, что средние значения норм расхода бензина марок А и В на 100 км пути совпадают, принять не можем, расхождение между и не объясняется только естественным разбросом данных.

4. Заметим, что если бы разброс Q оказался бы много больше, например, вдвое, то знамена-тель увеличился в 1,41 раза и изменился бы и наш вывод – при таком большом разбросе расхож-дение между эмпирическими средними уже объяснялось бы естественным разбросом данных, а не расхождением теоретических средних.

5. Проверяем гипотезу о том, что . С помощью нижней строки таблицы 6 распреде-ления Стьюдента решаем уравнение:

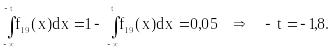
Так как –2,7 < –1,8, то гипотеза с уровнем доверия 0,95 может быть принята. По таблице видно, что эта гипотеза заслуживает доверия, которое можно оценить даже выше – в 99 %.

Вывод. Средний расход бензина на 100 км для марки В больше, чем для марки А, с уровнем доверия 99 %.