2.7 Связь между точностью и надежностью оценки

Для того, чтобы оценить точность и надежность точечной оценки для генерального среднего, воспользуемся тем, что статистика имеет нормальное распределение с математическим ожида-нием а и среднеквадратическим отклонением .

Напомним о некоторых свойствах величины 

Выполним над величиной операцию, которая называется нормировкой. Вычтем из нее а и поделим эту разность на . Из свойств математического ожидания и дисперсии следует, что математическое ожидание новой случайной величины будет равно 0, а ее среднеквадратическое отклонение – единице:

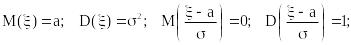
Величину N(0,1) с нулевым средним и единичной дисперсией называют стандартной нор-мальной. Ее плотность вероятности задается формулой:

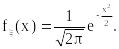
Как для N(0,1), так и для , вероятность попадания в любой интервал может быть выражена через функцию Лапласа (x):

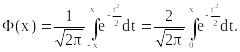
Для нее разработаны таблицы. В нашем руководстве это таблица 4 приложения 3. В силу очевидного из анализа соотношения (–х) = - (х) значения функции Лапласа в таблице заданы только для положительных x.

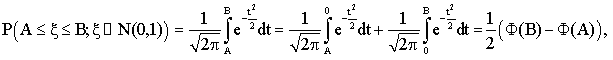
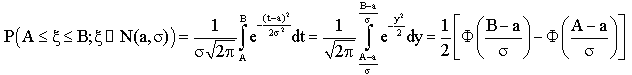
(сделали замену переменных) .

В частности для интервала, симметричного относительно математического ожидания а:

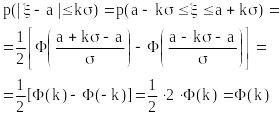
Из этой формулы вытекает так называемое правило трех  (рисунок 2.1).

Рисунок 2.1

То есть, практически достоверно то, что нормально распределённая величина примет значе-ние, отличающееся от её математического ожидания по модулю не более чем на 3, иначе говоря, “практически невозможно” появление значения, выходящего за пределы этого интервала.

Последнее обстоятельство находит широкое применение в различных приложениях.

Понятие “практически невозможно” и противоположное ему понятие “практически досто-верно” часто (особенно в экономике) используются в смягченном варианте, когда “практически достоверными” считаются уже события, вероятность которых не 0,997, а 0,95. То есть в экономике обычно используется “правило двух ”, так как

Введем обозначение k_ для корня уравнения:

Р_Р-___где 

Для случайной величины так же, как мы выводили правило трех , можно вывести формулу:

р-__

(в частности, для = 0,95 k_0,954 = 2 – она обращается в правило двух , а для  = 0,997 k_0,997 = 3 – в правило трех ).

Пример 2.7. Затаривание мешков с сахаром производится без систематических ошибок. Случайные ошибки подчинены нормальному закону со среднеквадратическим отклонением  = 200 г и, вследствие отсутствия систематической ошибки, математическим ожиданием 0. Найти вероятность того, что затаривание будет проведено с ошибкой, не превосходящей по абсолютной величине 400 г.

Решение. В задаче рассматривается случайная величина – ошибка взвешивания, то есть разность (– a) между случайным значением веса мешка сахара и его нормативным значением a – математическим ожиданием. Требуется найти:

.

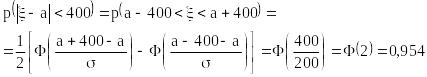Это типичная задача курса теории вероятностей.

Легко видеть, что одновременно мы решили и следующую задачу: какую максимальную ошибку затаривания мы можем гарантировать с вероятностью 0,95? Ответ: 2 = 400 г (лишь у 5 % мешков ошибка веса окажется больше). А если мы хотим определить максимальную ошибку недовеса-перевеса, в которую укладываются не 95 %, а “почти все” мешки (99.7 % мешков), то какова она? Ответ: 3= 600 г.

Заодно мы решили и задачу о том, как обеспечить требуемую точность: какую среднеквад-ратическую ошибку должен иметь автомат, проводящий затаривание, чтобы с вероятностью 0,95 ошибка перевеса-недовеса не превосходила 100 г? Ответ: 50 г.

Вторая и третья постановка вопроса характерна для задач математической статистики. В задачах математической статистики требуется не по интервалу находить вероятность попадания в него, а по заданной вероятности ищется интервал, обладающий некоторыми свойствами, в который с заданной вероятностью  попадает случайная величина. Для ~N(0,1), если ищется симметричный относительно 0 интервал, в который с вероятностью  попадает x, этот интервал равен [–k_,k_]) (рисунок 2.4).

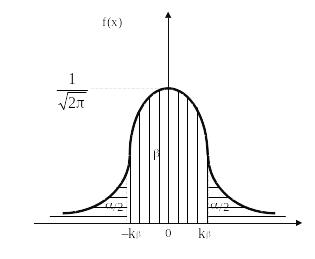
Рисунок 2.4

Тем самым, для определения надежности оценки мы пользуемся свойствами и таблицами нормального распределения. Если мы хотим иметь надежность, равную , то в таблице нормаль-ного распределения находим число k_, такое что:

(при этом надо помнить, что в данном случае по значению функции ищется значение аргумента).

Например, k_0,95 =1,96; k_0,997 = 3 (вспомните правило 2и 3).

Если требуемая надежность равна 0,9; 0,95; 0,98; 0,99 или 0,997 (а это самые распространенные на практике значения), то проще воспользоваться таблицей 5 приложения 3, задающей значения k_b нормального распределения для перечисленных значений .

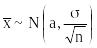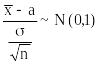Итак, в силу того, что , и , имеем:

.

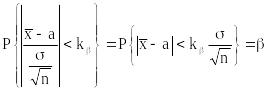Эта формула описывает точность, с которой значение описывает генеральное среднее а и надежность этой оценки (уровень доверия к ней).