Теорема Лагранжа.
Теорема Ролля является частным случаем теоремы Лафанжа.
Теорема Лагранжа. Пусть функция у =f(x) удовлетворяет следующим условиям:
1) непрерывна на отрезке [а, Ь]\
2) дифференцируема на интервале {а, Ь).
Тогда внутри отрезка существует по крайней мере одна такая
точка
в которой производная равна частному
от деления
приращения функции на приращение аргумента на этом отрезке, т.е.
Теорема Коши.
Если
функции 
и 
непрерывны
на отрезке [a,b],
дифференцируемы на интервале (a,b),
причем 
во
всех точках этого интервала, то найдется
хотя бы одна точка 
такая,
что
Замечание. Теорема Лагранжа — частный случай теоремы Коши
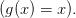
Замечание. Теорему Коши нельзя получить используя теорему Лагранжа отдельно к числителю и к знаменателю.
Правило Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных {конечному или бесконечному), если последний существует в указанном смысле.
Экстремумы функций одной независимой. Необходимые и достаточные условия существования экстремумов.
Определение 1.
Точка
называется тонкой максимума функции
,если в некоторой окрестности точки
выполняется неравенство
Определение 2.
Тонка
называется
тонкой минимума функ-
ции
если
в некоторой окрестности тонки
выполняется
неравенство
Значения функции в точках
и называются соответственно максимумом и минимумом функции.
Максимум и минимум функции объединяются общим названием
экстремума функции.
Экстремумы функций одной независимой. Необходимые и достаточные условия
существования экстремумов.
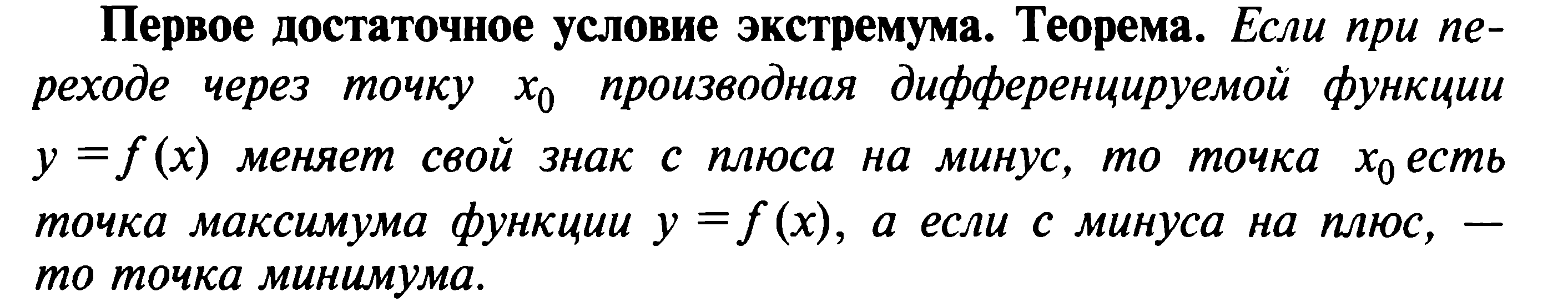
Вогнутость и выпуклость функций, точки перегиба функций.
Необходимые и достаточные условия существования точек перегиба функции.
Выпуклость и вогнутость графика функции в точке (аналитический признак).
Вот это ваще не знаю, то или нет. Но ничего другого я сюда запихнуть не могу
План исследования и построения графиков функций.
Приложение производной.
Приложение производной в экономической теории.
