5.3.2. Динамические методы определения модулей упругости

Для определения модуля упругости используется метод изгибных колебаний. Суть этого метода заключается в том, что образец одним концом жестко закрепляется, а к другому концу прикладывается изгибающая нагрузка, не вызывающая пластической деформации, рисунок 27.

После снятия нагрузки, учитывая упругость образца он будет колебаться с определенной частотой. Частота колебаний с затухающей амплитудой будет регистрироваться на фотобумаге. На основании записанной диаграммы колебаний определяется частота колебаний. Зная частоту представляется возможным рассчитать модуль упругости по формуле:

Для образца круглого сечения:

, где:

l – длинна образца;

m – масса образца;

d – диаметр образца;

f – частота колебаний.

Для образца прямоугольного сечения:

, где:

l – длинна образца;

h – высота образца в плоскости колебаний;

b – ширина образца;

m – масса образца;

f – частота колебаний.

Для определения модуля сдвига используют метод крутильных колебаний. Суть этого метода заключается в том, что образец одним концом жестко закрепляется, а к другому подвешивается маятник в виде равноплечного рычага с грузами. На оси маятника закрепляется оптическое зеркало. Маятник закручивает образец упруго на определенный угол и отпускается. При этом маятник будет колебаться с определенной частотой. Частоту колебаний фиксируют с помощью оптической системы, позволяющей записать частотную кривую колебаний, рисунок 28.

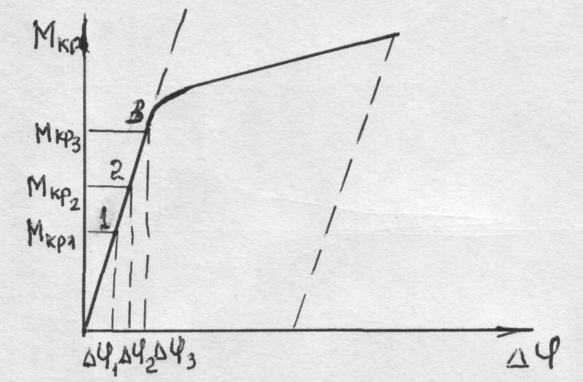
Рис. 26. Диаграмма кручения

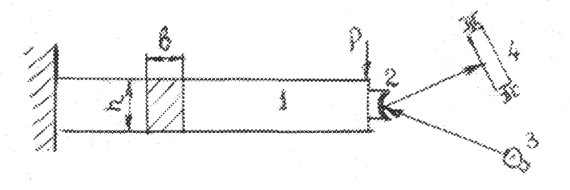
Рис.27. Схема испытания на изгиб: 1 – образец, 2 – оптическое зеркало, 3 – осветитель, 4 – барабан с фотобумагой

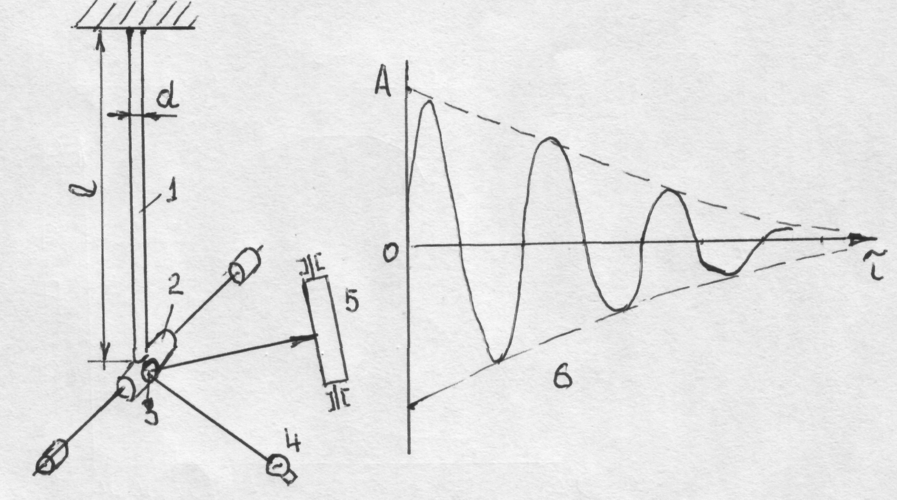
Рис.28. Схема испытания модуля сдвига: 1 – образец, 2 – маятник, 3 – зеркало, 4 – осветитель, 5 – барабан для записи колебаний, 6 – частотная кривая

На основании частотной кривой определяется частота колебаний образца и рассчитывается величина модуля сдвига по формуле:

, где:

l – длина образца;

d – диаметр образца;

I – момент инерции скручивающей системы;

f – частота колебаний.

Наряду с рассмотренными методами в практике определения модулей упругости широко используется импульсный метод, в основе которого лежит определение скорости распространения упругих волн, длина которых мала по сравнению с длиной образца. Частота волн принимается равной приблизительно 1МГц.

Скорость распространения волн определяется модулями упругости материала. Для определения волн:

Для поперечных волн:

, где:

Е – модуль упругости;

μ – коэффициент Пуассона;

G – модуль сдвига;

ρ – плотность материала;

υ – скорость распространения упругих волн.

Величину коэффициента Пуассона определяют рентгенографическим методом, путем измерения параметров решетки вдоль и поперек волн.

6. Неупругость металлов и сплавов

Абсолютно упругих материалов в природе нет. О неупругости

конструкционных материалов известно давно, но это явление считалось нежелательным и с ним старались бороться. Однако, позже, с началом развития машиностроения и особенно приборостроения, на него обратили серьезное внимание. Без учета неупругости конструкционных материалов невозможно производство сверхточных измерительных приборов.

Интерес к неупругому поведению металлов связан по крайней мере с двумя причинами.

Во-первых, способностью материалов к рассеиванию энергии в процессе нагружения в упругой области деформации, то есть при отсутствии необратимой пластической деформации. В ряде случаев требуется применение материалов, обладающих демпфирующей способностью – способностью гасить колебания. Это свойство используется в изделиях,

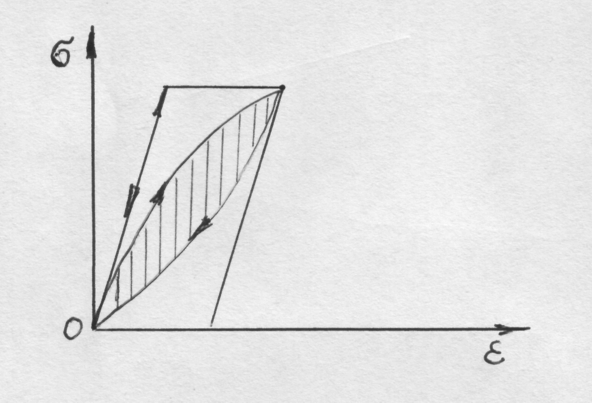
Рис. 29. Зависимость деформации от напряжения

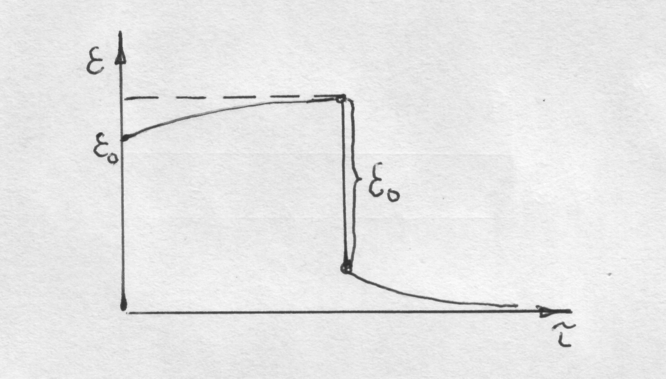
Рис.30. Схема изменения деформации во времени под действием постоянной нагрузки

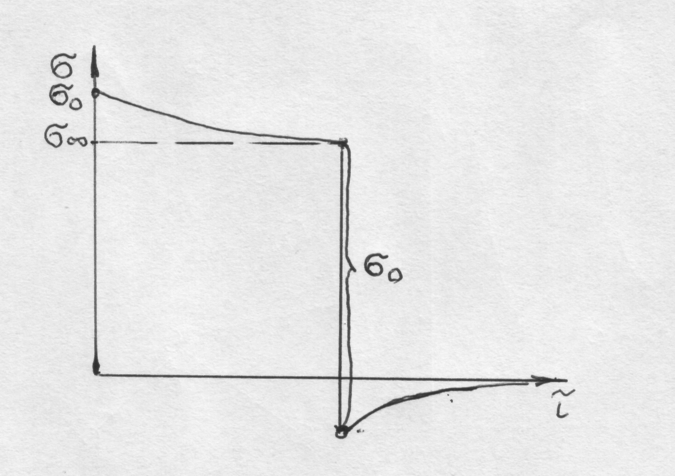
Рис.31. Схема изменения напряжений во времени

которые по своему назначению призваны поглощать энергию колебаний – рессоры, пружины, торсионные валы и др.

Во-вторых, способность материалов рассеивать энергию в ряде случаев крайне нежелательна, так как это может привести к увеличению инерционности и снижению точности измерительных приборов. Наряду с этим важно знание процессов ответственных за это рассеивание энергии колебаний.

В реальных металлах и сплавах неупругость проявляется при напряжениях значительно более низких, чем макроскопический предел упругости. Это означает, что при напряжениях не вызывающих остаточной деформации наблюдается отклонение от чисто упругого поведения металлов, так как линии нагрузки и разгрузки на диаграмме не совпадают, а образуют петлю гистерезиса, рис.29.

Площадь петли гистерезиса определяет величину рассеянной энергии за один цикл нагружения.

Классическая теория упругости устанавливает связь между напряжением и деформацией в предположении, что нагружение производится бесконечно медленно, так что деформируемое тело последовательно проходит ряд равновесных состояний. В этом случае энергия запасенная при нагружении будет полностью выделяться при разгрузке и рассеивание энергии будет отсутствовать.

В действительности это не так. Было показано, что при мгновенном нагружении реального тела оно мгновенно испытает деформацию равную ε₀, рис.30. Если тело оставить под нагрузкой, то оно испытает дополнительную деформацию до ε_∞. Если же мгновенно снять нагрузку, то деформация возвратиться на величину ε₀ и не будет равна 0. последующая выдержка без нагрузки будет сопровождаться дальнейшим уменьшением деформации до 0.

Аналогичная картина будет наблюдаться и в случае, если нагружение вести таким образом, что мгновенно фиксируется деформация ε₀. в этом случае напряжение скачкообразно повыситься до σ₀ (рис.31), а затем в процессе выдержки понизится до σ_∞.

При этом напряжения после снятия деформации могут понизиться так, что поменяют знак.

Последующая выдержка приведет напряжения к нулю.

Рассмотренные случаи указывают на то, что для описания поведения металлов под нагрузкой необходимо учитывать временную зависимость напряжения и деформации

σ(τ)=Еε(τ)

Согласно формальной теории неупругости, предложенной Зимером, соотношение между напряжением и деформацией приближенно выражается уравнением:

, где

,

σ – действующее напряжение

ε – величина деформации

а₁, а₂, b₁, b₂ – коэффициенты.

Твердое тело, поведение которого при нагружении описывается выше приведенным уравнением, называется стандартным линейным телом.

Если соотношение между напряжением и деформацией при одноосном растяжении идеально упругого тела характеризуется одним числом – модулем упругости, то для установления такой связи в случае стандартного линейного тела необходимо знание трех независимых постоянных, полученных путем деления всех коэффициентов на первый коэффициент .

С учетом этих постоянных уравнение стандартного линейного тела можно привести к виду:

, где:

- время релаксации при ε=Const

- релаксированный модуль упругости, то есть модуль определенный после завершения релаксационных процессов

- время релаксации при σ=Const.

Действительно, если мгновенно приложить напряжение σ₀ (τ=0), то согласно выше приведенному уравнению получим:

Решение этого уравнения дает:

При τ=0, деформация ε(τ)=ε₀, то есть она мгновенно достигнет величины равной ε₀, рис.30, а при τ=∞ деформация и достигается равновесные значение деформации, определяемое по закону Гука.

Для установления связи между напряжением и деформацией до начала процессов релаксации, необходимо найти предел отношения малого приращения напряжения (Δσ) к малому приращению деформации (Δε) за малый промежуток времени (Δτ).

После интегрирования уравнения стандартного линейного тела по времени получим:

Откуда: , где

- нерелаксированный модуль упругости

, М_н > М_р

М_н – М_р=ΔМ – дефект модуля упругости.

Дефект модуля упругости связан с процессами релаксации протекающими в области упругой деформации. К таким процессам следует отнести:

1. колебательное движение дислокаций,

2. термическую диффузию,

3. проскальзывание по границам зерен и др.

Под действием прикладываемых напряжений, не превышающих предел упругости, дислокации, закрепленные примесными атомами или узлами сетки Франка, будут осуществлять колебательное движение. Указанные колебательные движения дислокаций будут приводить к рассеиванию энергии.

Наряду с этим под действием напряжений возможно перемещение точечных дефектов – примесных атомов внедрения и замещения, вакансий и др. Это также будет сопровождаться рассеиванием энергии.

Рассеивание энергии возможно также и в результате термической диффузии. Известно, что при деформации в сжатой области повышается температура, а в растянутой – понижается. В результате этого тепло будет перетекать от сжатой области к растянутой. Если бы скорость теплопроводности была велика по сравнению со скоростью колебаний, то температура стержня оставалась бы постоянной. Поскольку это не так, поток тепла приводит к возникновению компоненты деформации, которая не находится в фазе с упругой деформацией. Следствием этого будет рассеивание энергии и изменение модуля упругости.

В поликристаллических материалах каждое зерно деформируется не так как окружающие зерна и неупругость возникает за счет проскальзывания по границам зерен.