5.1. Вывод элементарного закона на основе анализа взаимодействия атомов в кристаллической решетке

Представим схему упругого взаимодействия в виде двух атомов в кристаллической решетке, рис.21.

Два соседних атома в решетке металла, неподверженных действию внешних сил, свободного от внутренних напряжений, находятся в состоянии покоя, когда силы притяжения уравновешены силами отталкивания. Силы взаимодействия атомов в функции расстояния между ними изменяются в соответствии с кривыми, рис.22.

Согласно кривой 1 приближение одного атома к другому увеличивает силу притяжения и на определенном расстоянии резко нарастают силы отталкивания (кривая 2). Пересечение результирующей кривой 3 с горизонтальной осью определяет равновесное состояние между атомами.

Энергия связи между атомами также зависит от расстояния между атомами и описывается аналогичным графиком, рис.23.

На бесконечно большом расстоянии энергия связи приближается к нулю. По мере сближения атомов совершается работа, величину которой вычитаем из исходной нулевой энергии. В результате получаем кривые характеризующие изменение энергии притяжения 1, отталкивания 2 и результирующей 3, минимум которой соответствует равновесному состоянию.

Смещение атомов из положения равновесия характеризуется разностью межатомных расстояний:

В случае растяжения > и U положительно, при сжатии < и U отрицательно.

Условие равновесия можно записать в виде:

При малой величине смещения dU совершается работа FdU, которая компенсируется изменением энергии взаимодействия

Для вывода закона Гука необходимо соблюдение трех условий:

1. непрерывность функции Е(U),

2. минимум 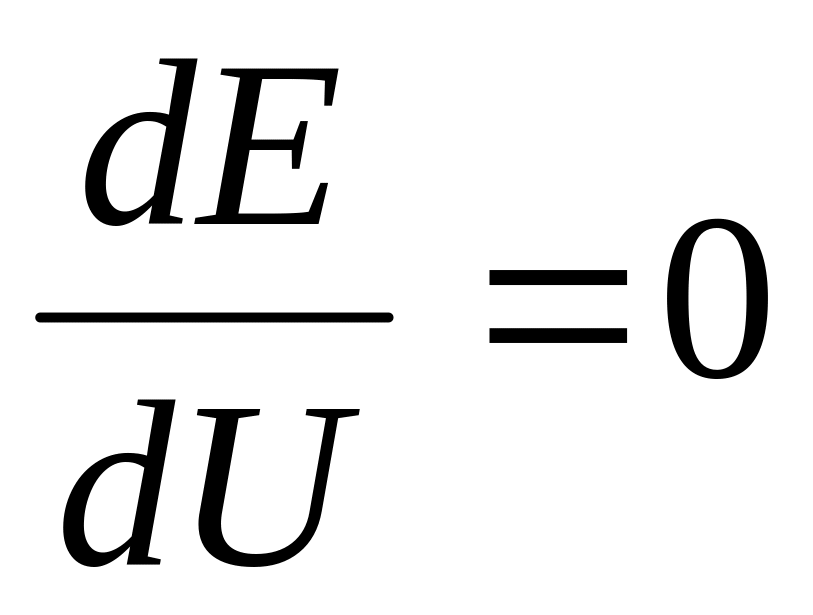при U=0,

3. смещение U<<

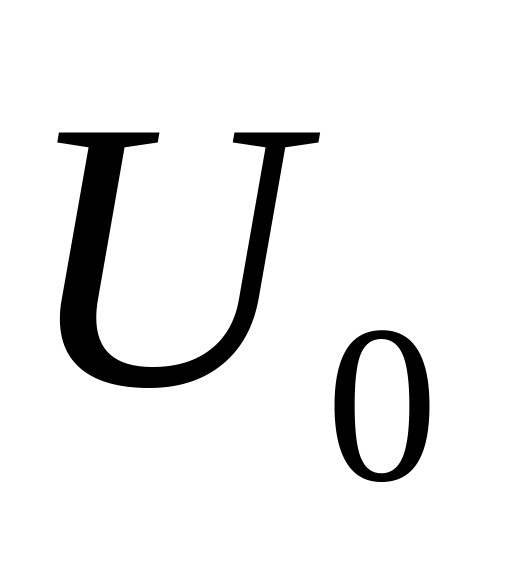
Первое условие позволяет разложить функцию энергии по величине смещения U в ряд Тейлора.

…, где

- энергия взаимодействия между атомами при U=0.

Поскольку при U=0 членами в третьей и более высоких степеней в ряду Тейлора можно пренебречь.

Отсюда:

Вторая производная - кривизна функции Е(U) в точке а₀ и она не зависит от расстояния и является константой. Тогда:

Это и есть элементарный закон Гука

F – внешнее усилие, которое прикладывается к решетке;

U – величина смещения, определяющая деформацию;

Сonst – модуль упругости.

Полученная зависимость справедлива для малых величин смещений. При больших смещениях в ряду Тейлора членами в третьей и большей степени пренебречь нельзя, материал выходит из области упругости и начинается пластическая деформация, для которой эта зависимость не справедлива.

5.2. Влияние различных факторов на модули упругости

Учитывая то обстоятельство, что модули упругости связаны с величиной сил межатомного взаимодействия, а последние зависят от расстояния между атомами в кристаллической решетке, влияние температуры на модули упругости следует рассматривать с этих позиций. Известно, что все металлы и сплавы при нагреве расширяются, а при охлаждении сужаются. Термическое расширение объясняется изменением расстояния между атомами, а это должно приводить к изменению величины сил межатомного взаимодействия.

Экспериментальные исследования модулей упругости при нагреве показали, что с повышением температуры величина модулей упругости уменьшается. Для чистых металлов не претерпевающих полиморфные превращения связь модулей упругости с температурой близка к линейной. Примером таких металлов могут служить медь, никель и др., рис. 24.

При наличии полиморфных превращений в металлах при достижении температуры полиморфного превращения модуль упругости изменяется скачкообразно (пример железо). До 910^О железо существует в виде модификации Fe_α, при нагреве Fe_α параметр решетки непрерывно увеличивается и это будет сопровождаться понижением модуля упругости. При достижении температуры 910^ОС Fe_α→Fe_γ, что сопровождается перестройкой решетки ОЦК в решетку ГЦК. В результате этого превращения расстояния между атомами резко уменьшается и модуль упругости повышается. По мере дальнейшего нагрева имеет место обычное термическое расширение и понижение модуля упругости. На модуль упругости сплавов существенно влияют и фазовые превращения, протекающие при нагреве и охлаждении (пример превращений П А, А→М и другое).

Следующим фактором, влияющим на модуль упругости является наклеп в результате пластической деформации. Влияние этого фактора менее существенно чем температуры. Холодная пластическая деформация сопровождается возникновением текстуры деформации, кристаллическая решетка удлиняется в направлении деформации и сужается поперек деформации. Изменения модулей упругости, связанные с образованием текстуры, могут достигать десятков процентов. Для изотропного состояния деформация способствует уменьшению модуля упругости менее чем на 1%.

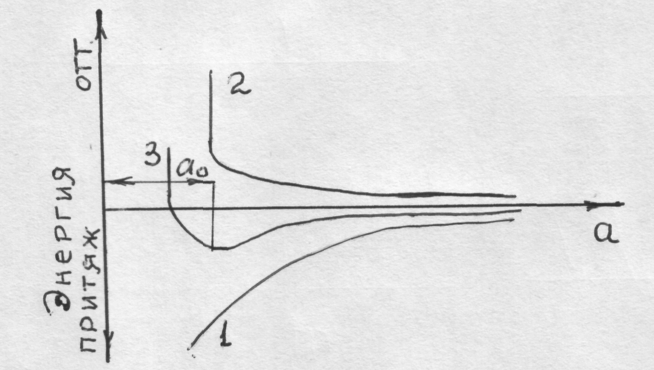
Рис. 23. Изменение энергии взаимодействия между атомами в зависимости от расстояния между ними

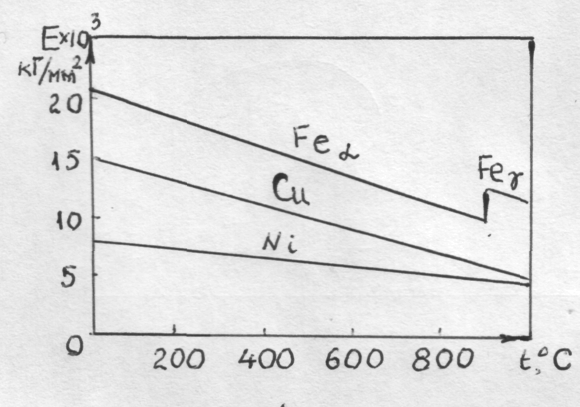
Рис. 24. Влияние температуры на модуль упругости листов

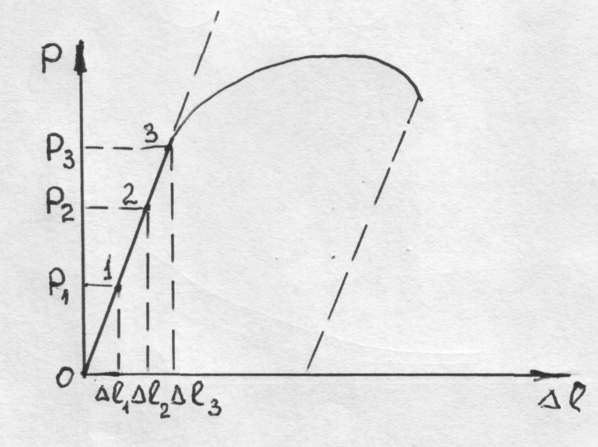
Рис. 25. Диаграмма растяжения

Влияние легирования на модуль упругости подобно влиянию температуры и определяется в основном влиянием легирования на величину межатомного расстояния и изменение сил межатомного взаимодействия.

Рентгенографические исследования влияния легирования на параметр кристаллической решетки растворителя показали, что он изменяется почти линейно с концентрацией растворенного элемента. При этом следует отметить, что модуль упругости при легировании может как повышаться, так и понижаться. Все определяется взаимным соотношением между силами связи атомов растворенного элемента с атомами растворителя и силами связи между атомами растворителя. Если величина первых превышает величину вторых, то легирование будет сопровождаться увеличением модуля упругости.

Наряду с этим при легировании возможно образование новых фаз. Если модуль упругости образующей фазы превышает модуль упругости фазы, из которой она образуется, то модуль упругости будет повышаться при легировании. При этом для ряда сплавов следует отметить аномальное температурное поведение модулей упругости, связанное с магнитными эффектами. Примером таких сплавов является элинвар, у которого в определенном температурном интервале (-50÷+50^ОС) модуль упругости остается постоянным.