5. Упругость и упругие свойства материалов

Одной из важнейших задач науки о механических свойствах металлов и сплавов является установление закономерностей, связывающих напряжение с соответствующими деформациями.

Связь между напряжением и деформацией сложная и определяется в основном экспериментально при помощи специальных машин для испытания механических свойств, обеспечивающих постоянную скорость деформации и регистрирующих усилие и деформацию.

В качестве примера рассмотрим диаграмму растяжения, полученную при растяжении цилиндрического образца, рис.20. Эта диаграмма растяжения включает три участка.

I -характеризуется прямой пропорциональностью между нагрузкой и деформацией. На этой стадии имеет место упругая (обратимая) деформация.

II-характеризуется большей величиной деформации при уменьшающейся нагрузке. При этом деформация равномерна распространяется по всей длине.

III-характеризуется потерей устойчивости деформации, на образце образуется шейка. Дальнейшее развитие неоднородной деформации закончится разрушением.

Закономерности упругого поведения материалов в первые были изучены Гуком и заключаются в следующем:

1. Увеличение длины образца (при растяжении) прямопропорционально нагрузке при постоянной начальной длине и нагрузке.

2. Увеличение длины прямопропорционально начальной длине образца при постоянной нагрузке и сечении.

3. Увеличение длины образца обратнопропорционально сечению образца при постоянной нагрузке и длине.

Эти закономерности можно представить математически:

Разделив обе части уравнения на получим:

, где:

- величина действующего напряжения

- величина относительной деформации.

Следовательно, можно записать:

Const=E – модуль упругости при одноосном растяжении.

Приведенное выражение является элементарным законом Гука, устанавливающим связь между прикладываемым напряжением и деформацией.

Под действием касательных напряжений будет осуществляться аналогичная связь:

τ=G∙g, где:

τ – касательное напряжение

g – величина упругого сдвига

G– коэффициент пропорциональности, физический смысл которого – модуль сдвига.

Согласно элементарному закону Гука величина Е и характеризуются углом наклона диаграмм растяжения и кручения к оси удлинений и сдвигов.

Модуль упругости не зависит от знака деформации, его величина будет постоянной при растяжении и сжатии.

Чем больше Е, тем круче возрастает напряжение с ростом упругой деформации. Более правильно относить модуль упругости не к 100%, а к одному 1% деформации и удобнее оперировать с величиной обратной модулю упругости , называемой коэффициентом нормальной упругости. Модуль нормальной упругости , характеризует упругую деформацию, вызываемую изменением напряжения на 1 .

Рис. 19.Схема деформации цилиндрического стержня при сжатии: а - до приложения нагрузки; б – после приложения нагрузки

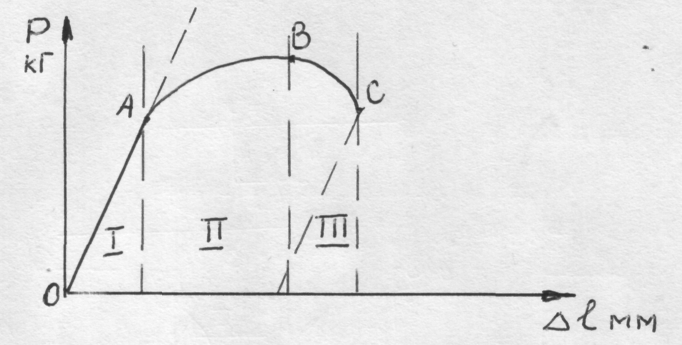
Рис. 20. Диаграмма растяжения

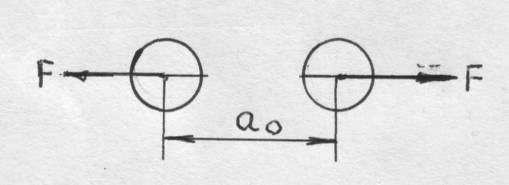
Рис. 21.Схема упругого взаимодействия атомов в кристаллической решетке

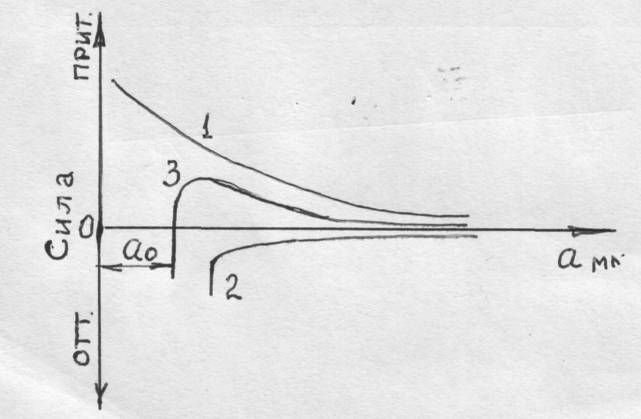
Рис. 22.Изменение величины сил взаимодействия между атомами в зависимости от расстояния

Как было отмечено выше элементарный закон Гука применим лишь для случая одноосного напряженного состояния. Экспериментально показано, что действие одноосного напряженного состояния вызывает трехосную деформацию. Поперечная деформация при упругом растяжении характеризуется коэффициентом Пуассона „μ”, равным отношению поперечной к продольной деформации, взятым с обратным знаком. Для большинства металлов и сплавов значение коэффициента Пуассона меняется в пределах 0,25÷0,35 в зависимости от природы металлов и сплавов.

Ввиду того, что реальные испытывают объемную деформацию, описание упругой деформации с помощью элементарного закона Гука будет неполным и необходимо установить связь между деформациями и напряжениями во всех направлениях. Сущность обобщенного закона Гука сводится к тому, что устанавливается линейная зависимость не только между одним главным напряжением и удлинением в этом направлении, а каждой компонентой тензора напряжений и каждой компонентой тензора деформации.

Если к упругодеформированному телу приложено напряжение , которое вызывает удлинения , , , то каждое из этих удлинений связано линейной зависимостью с напряжением.

Если в качестве осей координат выбрать главные направления, то касательные составляющие тензора напряжений и величины сдвигов обратятся в нули и останутся только три главных напряжения и три главных удлинения.

В этом случае обобщенный закон Гука будет учитывать влияние на каждое из удлинений в трех направлениях каждое из трех главных напряжений.

Если , то в этом случае получим элементарный закон Гука

Отсюда следует, что удлинение в направлении оси х может быть вызвано если , действием напряжений в направлении осей y и z.

В общем случае закон Гука, для случая действия нормальных напряжений, можно представить в виде:

Для сдвигов, в условиях действия касательных напряжений, обобщенный закон Гука записывается в виде:

Не менее важна форма обобщенного закона Гука, когда уравнения решаются относительно нормальных напряжений:

где G – модуль сдвига

χ – относительное изменение объема

Из приведенных зависимостей следует, что каждое напряжение у изотропного тела вызывает:

1. Изменение объема (λ∙χ)

2. Изменение формы , , в то время, как касательные напряжения вызывают лишь изменение формы без изменения объема.

С точки зрения практического применения обобщенного закона Гука наиболее широко используют зависимость между константами упругости изотропного тела (Е, G, К и μ)

, где:

Е – модуль упругости

G – модуль сдвига

К – модуль объемной сжимаемости

μ – коэффициент Пуассона.

Зная две константы материала, представляется возможное определить две другие расчетным путем.