20. Вязкость разрушения
20.1 Теоретическое обоснование методики определения вязкости разрушения
В недалеком прошлом расчеты деталей машин и конструкций на прочность базировались, как правило, на значения номинального разрушающего напряжения, определяемого при испытании на растяжение гладких образцов. Допустимое рабочее напряжение находят делением разрушающего напряжения на коэффициент запаса прочности.
Наблюдение катастрофических разрушений конструкций показали, что магистральная трещина, бегущая со скоростью более 1000 м/сек, возникает от исходных дефектов типа трещин (при сварке или других технологических операциях) при напряжении много ниже предела текучести. В связи с этим необходимо знать сопротивление материала распространению хрупкой трещины, чтобы установить допустимое напряжение по максимально возможному размеру трещины, имеющейся в конструкции до нагружения. Чтобы определить сопротивление росту хрупкой трещины на образцах и по результатам рассчитать конструкцию, используется линейная механика разрушения, анализирующая распределение напряжений у вершины трещины.
Учитывая наличие трещины, механика разрушения устанавливает количественную связь между действующим на тело напряжением, Формой и размерами трещины и сопротивление материала докритическому (стабильному) и закритическому (нестабильному) развитию трещины.
При наличии реальных трещин в металлах в момент испытания, меняется упругонапряженное состояние. Наличие такого напряженного состояния ограничивает величину зоны пластической деформации, материал становится охрупченным и трещина будет находиться в области плоской деформации.
По краям образцов пластическая деформация менее стеснена, радиус пластической зоны увеличивается, материал будет находится в плосконапряженном состоянии и разрушение обычно происходит по сдвиговому механизму с максимальным поглощением энергии.
Величину напряжений у вершины трещины выражают через коэффициент интенсивности напряжения Кс в момент перехода от стабильного (докритического) к нестабильному (закритическому) разрушению.
Величина
коэффициента интенсивности напряжений
Кс определяется
по формуле:
, где:
σF – номинальное разрушающее напряжение;
а – длина трещины.
и называется вязкостью разрушения при плосконапряженном состоянии.
Это уравнение справедливо при условии, что разрушение образца происходит без макропластической деформации материала в вершине трещины. Первоначально предполагалось, что при данной температуре и толщине образца величина Кс является константой материала. Однако последующие эксперименты показали, что Кс зависит от длины трещины и толщины образца. С увеличением толщины образца воздействие окружающего упругонапраженного материала ограничивает величину зоны пластической деформации, причем это воздействие наиболее ощутимо в середине образца. Радиус пластической зоны здесь минимален.
По краям образца пластическая деформация менее стеснена, радиус пластической зоны увеличивается, материал находится в плосконапряженном состоянии и разрушение происходит по сдвиговому механизму. Вязкость разрушения по сути дела должна определяться относительными размерами нормального и наклонного участков разрушения.
По данным испытания алюминиевого сплава была построена зависимость вязкости разрушения и доли нормального разрушения от толщины образца, рис. 121.
Согласно этому рисунку с увеличением толщины образца вязкость разрушения (Кс) резко снижается и асимптотически приближается к предельному значению вязкости разрушения в условиях плоской деформации(К1с).
Для толстых образцов стесненность пластической деформации максимальна и разрушение происходит полностью по нормальной к действующим напряжениям плоскости.
С уменьшением толщины образца по краям появляются наклонные поверхности сдвига. Отношение нормального к наклонному разрушению уменьшается, я вязкость разрушения Кс возрастет. В пределе достигается максимальная вязкость разрушения у тонких образцов, излом которых наклонен по одной или двум плоскостям, характерный для плосконапряженного состояния, рис.122.
Снижение вязкости разрушения, связано с уменьшением доли объема материала, охваченного пластической деформацией, наблюдается также в самых тонких листах. Для большинства металлов это снижение вязкости разрушения происходит при толщинах не представляющих практического интереса – фольги.
Между величиной вязкости разрушения при плосконапряженном и плоскодеформированном состоянии существует связь, установленная Ирвеном:
С учетом влияния толщины образца на вязкость разрушения вводится учитывающий это обстоятельство параметр βc:
,
где
Кс – вязкость разрушения при плосконапряженном состоянии;
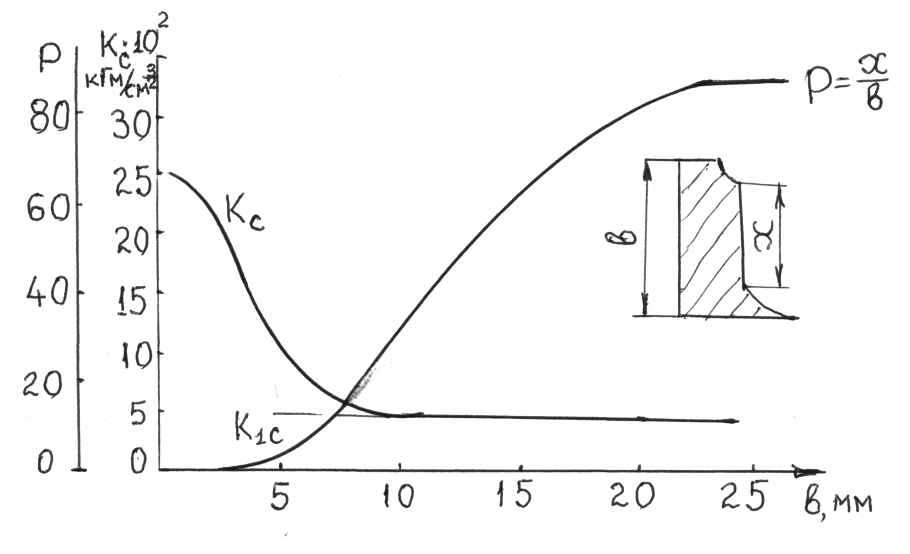
Рис.121. Зависимость вязкости разрушения КС и долей нормального излома (Р) от толщины образца
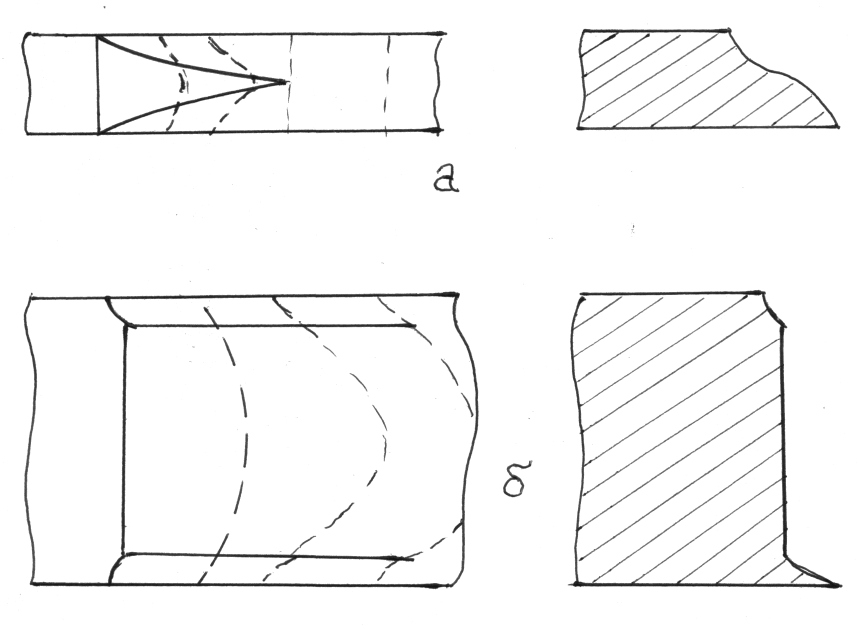
Рис.122. Зависимость вида разрушения от толщины образца: а) тонкий, б) толстый
в – толщина образца;
σT – предел текучести материала.
Если βc=2π, разрушение будет полностью сдвиговым.
Если βc>4, наклонные участки сдвига занимают более половины поверхности разрушения.
Если βc<1, языки сдвига будут очень малыми.