19.2.2 Экспериментальное определение раскрытия трещины

Существо методики определения критического раскрытия трещины сводится к испытанию образцов с надрезом, образцов с трещиной или образцов с нарезом и трещиной. Эскиз образца представлен на рис.113.

Образец по толщине соответствует толщине листа, из которого он вырезан.

Трещина зарождается в образце за 50000 циклов при напряжении в цикле , чтобы не допустить повреждение материала у вершины трещины.

Для определения критического раскрытия трещины образец нагружается со скоростью υ=2,5мм/сек напротив надреза. Образец устанавливается на ролики, чтобы устранить трение образца с опорами. Для определения раскрытия трещины в надрезе устанавливается механический датчик, позволяющий записывать диаграмму, рис.114.

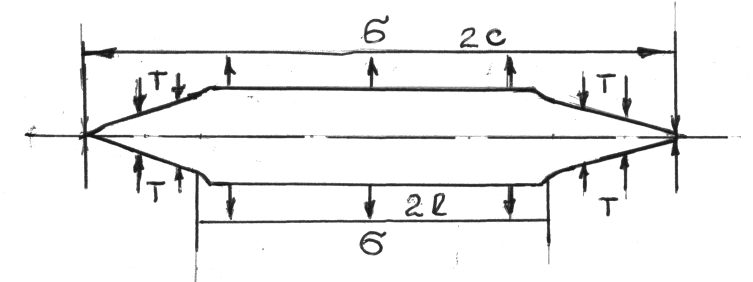
Рис.112. Модель трещины в бесконечной пластине

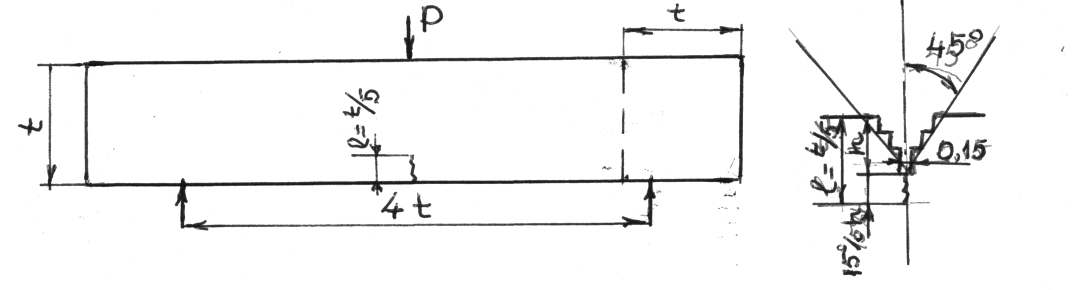
Рис.113. Эскиз образца и надреза с трещиной

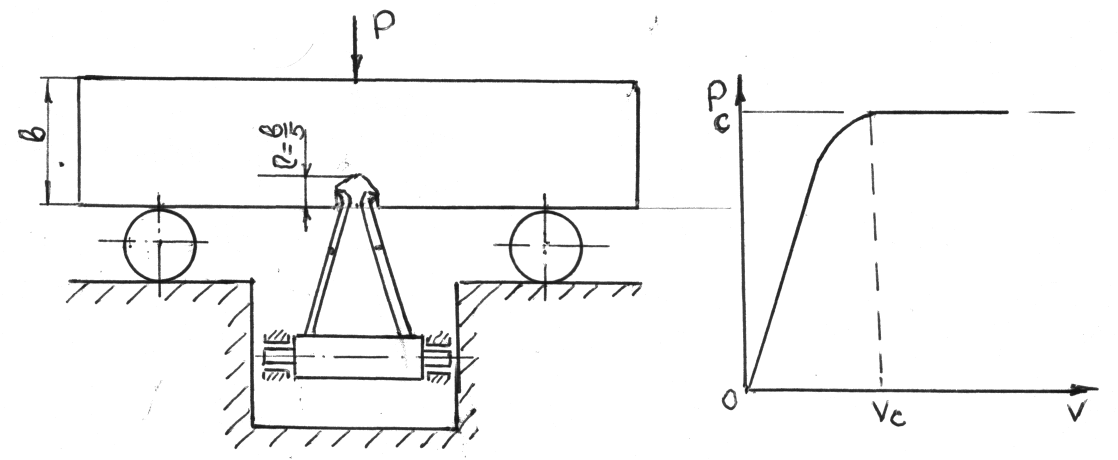
Рис.114. Схема испытания на критическое раскрытие трещины

Из диаграммы определяется Vс, величина перемещения берегов трещины и по формуле: , где:

z – расстояние от места замера перемещения до поверхности образца;

n – Const;

(в – e) – высота неповрежденной части образца;

е – глубина надреза.

вычисляется критическое раскрытие трещины δс.

Для образцов с трещиной регистрация раскрытия трещины фиксируется с помощью кинокамеры.

Данная методика, наряду с критическим раскрытием трещины, позволяет определить номинальное напряжение на фронте трещины, по формуле:

, где

М – изгибающий момент; W – момент сопротивления в поперечном сечении.

Наряду с этим представляется возможным определить вязкость разрушения, по формуле: , где

Рс – величина нагрузки, соответствующая началу развития трещины;

в – ширина образца;

h – высота образца у надреза;

, где ℓ - глубина надреза с трещиной.

19.3 Методика оценки сопротивления развитию усталостной трещины

Для изучения кинетики развития усталостной трещины используют образцы, размеры которых дают возможность изучать скорость развития трещины на достаточно длинном участке его траектории.

В качестве основной характеристики сопротивления металла развитию усталостной трещины принята зависимость скорости продвижения трещины от величины напряжения на её фронте. Эта зависимость имеет вид, рис.115.

На I участке зависимость скорости роста усталостной трещины от номинального напряжения может быть выражена:

, где

σс – напряжение старта; К – tgα.

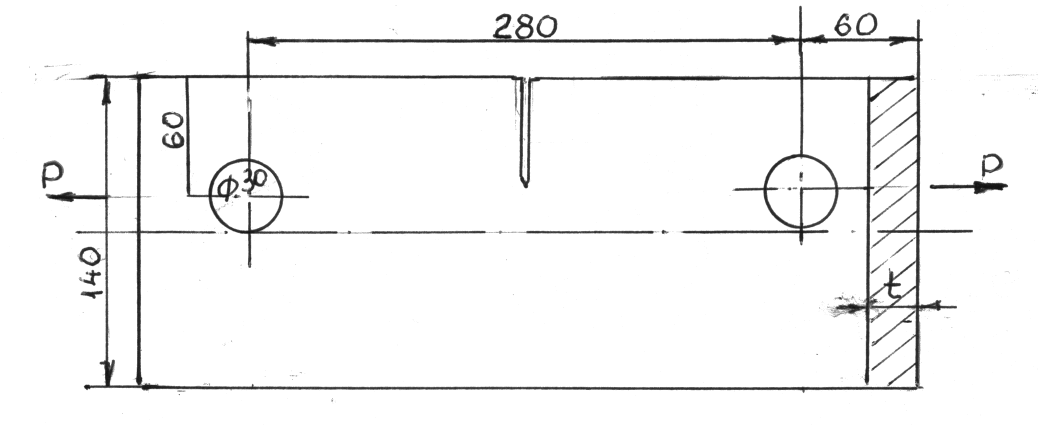
Рис.115. Эскиз образца: а=280 мм, в – 140 мм, с=60 мм, t – толщина листа, l – глубина надреза с трещиной

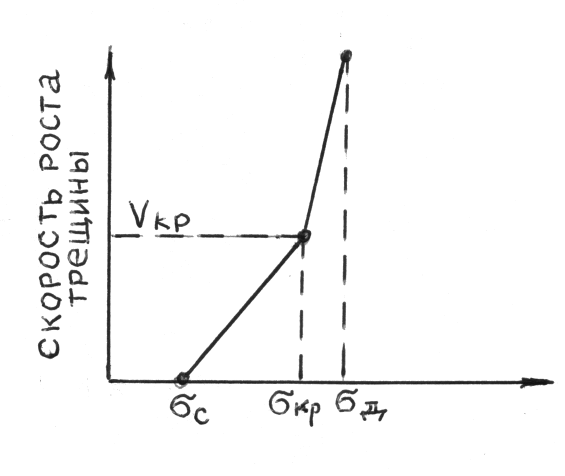
Рис.116. Зависимость скорости развития усталостной трещины от величины напряжения. σ_с – напряжения старта (начала развития трещины), σ_кр – критическая величина напряжения, σ_Д – напряжение долома

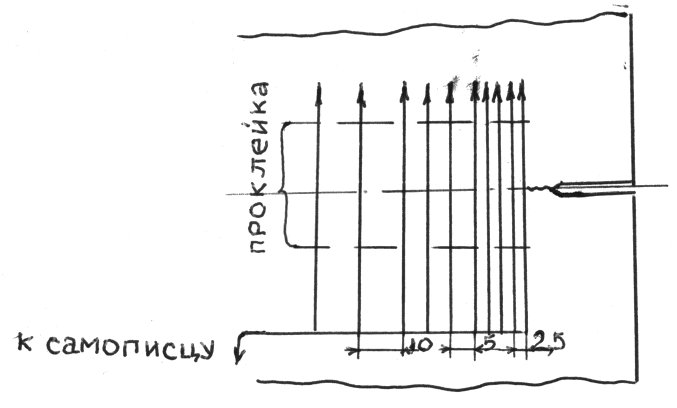
Рис.117. Схема наклеивания проволочного датчика

Используя параметры кинетической кривой роста усталостной трещины, можно производить расчет конструкции либо на полную надежность, используя в качестве допустимых напряжений σc, либо ограниченную надежность – σкр.

Основная сложность методики заключается в определении скорости роста усталостной трещины. Уральским отделением ЦНИИ МПС предложена следующая методика. На боковую поверхность образца наклеивается проволочный датчик, который через специальную схему подключается к самописцу, регистрирующему ступеньки соответствующие разрыву проволочек, рис.117.

Расстояние между ступеньками будет соответствовать числу циклов нагружения. Зная частоту приложения нагрузки, можно определить время и скорость развития трещины: .

Для середины указанных интервалов определяется номинальная величина напряжений по формуле:

, где

Р – нагрузка в цикле;

в, с, t, е – геометрические параметры.