19.2.1 Теоретическое и экспериментальное обоснование приложимости методики раскрытия трещины

Когда в той или иной конструкции предполагается использование новой стали, а данных об их разрушении в рабочих условиях нет, то самое лучшее решение задачи предотвращения хрупкого разрушения заключается в том, чтобы снабдить конструктора количественным критерием сопротивления материала хрупкому разрушению. Пока таких данных нет, конструкцию приходится рассчитывать по обычным показателям надежности с ущербом для экономии средств, поскольку по необходимости приходится брать более качественные материалы, делать элементы толще, чем это требуется на самом деле.

Для высокопрочных материалов характерно почти полное отсутствие пластической деформации перед разрушением, а их поведение до разрушения и внезапном разрушении близко к упругому. При наличии концентратора напряжений такие материалы разрушаются хрупко. Анализ распределения напряжений у вершины трещины в однородном поле напряжений позволяет вывести критерии сопротивления хрупкому разрушению. Обычно в качестве параметра сопротивления разрушению выбирают коэффициент интенсивности напряжений Кс, который в условиях плосконапряженного состояния удовлетворяет соотношению: Кс = Е·Q, где Е – модуль упругости; Q – удельная энергия разрушения (сила на распространение трещины) у вершины трещины.

Зависимость между Q, приложенным напряжением – σ и полудлиной трещины выражается уравнением Гриффитса:

Под действием внешних напряжений трещина неуклонно раскрывается и может медленно распространятся пока не возникнет критическое состояние, с достижение которого начинается быстрое разрушение. Этому моменту величину Q принимают за критическую Qс, выражая после этого критерий неустойчивости – σнеуст в виде:

.

К настоящему времени проведена значительная работа по теории механики разрушения и её практическому использованию. К сожалению результаты проведенных испытаний, с целью определения сопротивления разрушению при плоской деформации, таковы, что для многих материалов нельзя получить реальной оценки сопротивления разрушения к широкораспространенным на практике толщинам.

Когда течение металла у кончика трещины приведет к искажению основного поля напряжений упругости в его окрестности, анализ на основе линейной механики разрушение теряет силу. Однако в этих условиях наличие пластической деформации у вершины трещины делает возможным расхождение берегов трещины без прироста её длины. Такое относительное перемещение берегов трещины у её вершины называют раскрытием трещины.

В любой момент распространения разрушения ход процесса разрушения зависит только от материала у вершины трещины. Материал разрушается только потому, что местные условия в отношении напряжений и деформации у вершины трещины достигли определенного критического состояния, которое представляет собой характеристику материала. На основе анализа механики разрушения Гриффитсом предлагается равновесие между энергией освобождающейся при движении трещины и поверхностной энергией, идущей на образование новых берегов трещины. Когда трещина распространяется в пластичном материале, энергия расходуется не только на разрушение, но и на деформацию. При этом энергия, освобождающаяся при движении трещины, довольно точно равна поглощенной энергии: , где σт – предел текучести; δ – раскрытие трещины.

Когда протяженность пластической зоны мала по сравнению с длинной трещины, пластичность можно учесть, внеся небольшую поправку к длине трещины и проведя дальнейший анализ методами линейной механики разрушения. Такой подход предполагает, что способность нести нагрузку у конца “гинотектической” трещины большой длины в поле чисто упругих напряжений такая же, как у кончика реальной трещины в пластической зоне. Когда протяженность пластической зоны мала по сравнению с длинной трещины, анализ подобного рода дает своеобразное соотношение между раскрытием трещины, размером пластической зоны и коэффициентом интенсивности напряжений.

Анализ псевдопластичности возможен на основании модели течения в узком слое на продолжении трещины, рис.112.

Эта модель позволяет рассматривать зоны пластичности большей протяженности чем методами упругого анализа с поправкой к длине трещины. Эта модель рассматривает трещины длинной 2ℓ под действием однородного поля растягивающих напряжений σ по нормали к трещине. Под действием напряжений длинна трещины вместе с пластической зоной возрастает до 2с. Распространение и раскрытие трещины частично сдерживается равномерно распределенными внутренними напряжениями Т, действующими только на поверхности дополнительного разреза от х = ±ℓ до х = ±с.

Если Т=σт, то раскрытие трещины можно выразить:

бес

После разложения в ряд, получим:

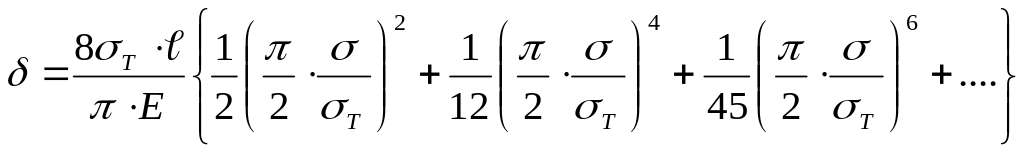
Оставив только первый член:

Поделив правую и левую часть уравнения Гриффитса на σт, получим:

Поскольку правые части уравнения равны, то: , а .

Эксперименты на основе модели течения в слое показывают, что при низких напряжениях зависимость соблюдается и что при напряжениях близких к σт, раскрытие у кончика трещины δ будет равно полному удлинению.

С выбором такой модели разумно предположить, что конструкция должна разрушаться подобно образцу, если пластическое течение у кончика трещины в конструкции эквивалентно течению в образце.

Если конструкция и образец имеют одинаковую толщину, условия их разрушения должны быть аналогичными.