4. Деформация и описание деформированного состояния

Под воздействием внешних нагрузок все материалы претерпевают деформацию, либо исчезающую после снятия нагрузки (упругую деформацию), либо остаточную (пластическую деформацию).

Дословный перевод слова „деформация” означает изменение формы, которая имеет место в большинстве случаев деформации, но не всегда. Например, при кручении цилиндрического стержня ни длина, ни диаметр практически не меняются. И в то же время образец претерпевает упругую и пластическую деформацию. Другим примером может служить гидростатическое сжатие или растяжение, при котором не происходит изменение формы.

В связи с этим, более точное определение деформации заключается в изменении расстояния между какими-либо точками деформированного тела.

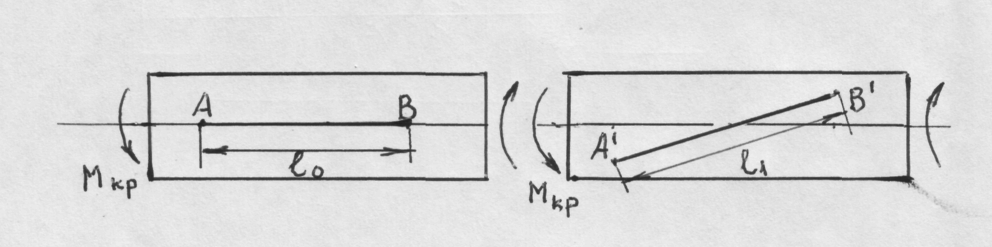
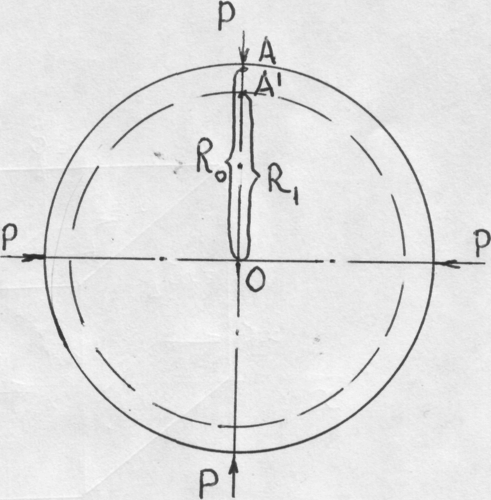
Применяя этот признак применительно к кручению, можно увидеть, что в направлении винтовой линии АВ расстояние между точками скручивающегося цилиндра меняется, также как и в сжимаемом шаре в радиальном направлении, рис.11, 12.

Исходя из этого следует заключить, что деформацию следует рассматривать как смещение от точки к точке.

Такое определение деформации позволяет объяснить наблюдающуюся неоднородность деформации при кручении и других видах деформации. Наглядное представление о неоднородности деформации можно представить в виде следующей схемы, рис.13.

Согласно рис.13 величина деформации, в соответствии с вышеприведенным определением деформации, при кручении будет неоднородна. Максимальную деформацию цилиндр испытает на поверхности и минимальную в центре, равную нулю, так как точка О при кручении не сместилась.

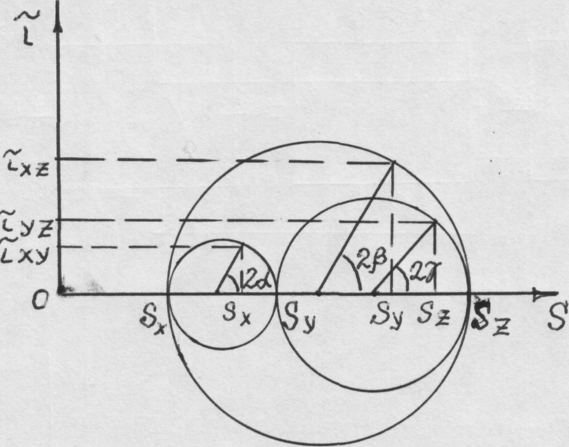
Рис. 10. Схема кругов Мора для случая объемного напряженного состояния

>

Рис. 11. Схема деформации цилиндра при кручении

>

Рис. 12. Схема деформации шара при гидростатическом сжатии

Ввиду того, что установление связи между внешними нагрузками (напряжениями) и деформацией является основной задачей науки о прочности и деформации, разберем детально характеристики деформации подобно напряжениям.

Для анализа деформации рассмотрим случай осевого растяжения стержня. Под действием приложенной нагрузки стержень деформируется – увеличивается в длине и уменьшается в диаметре. При этом следует различать условную и истинную деформацию. Для определения условной или относительной деформации необходимо знать начальные и конечные размеры образца, рис.14.

Условная деформация определяется по формуле:

, где

ε – относительное удлинение;

- начальная длина;

- конечная длина.

, где

ψ – относительное поперечное сужение;

- начальное поперечное сечение;

- конечное поперечное сечение.

Для определения истинной деформации необходимо разбить весь процесс деформации на ряд этапов ( , , , ,… и т.д.), рис.15.

В этом случае удлинение стержня будет складываться из удлинений на участках.

; ; …. , , где

- истинная деформация на участках.

Истинная деформация стержня будет определяться как сумма истинных деформаций на участках:

Уменьшая длину участков деформации, истинная деформация стержня будет интегральной величиной:

.

Между условной и истинной деформацией существует определенная связь:

, откуда

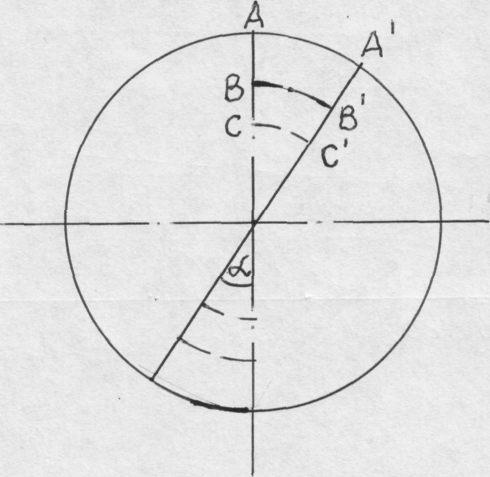
Рис. 13. Схема деформации цилиндра при кручении по диаметру цилиндра

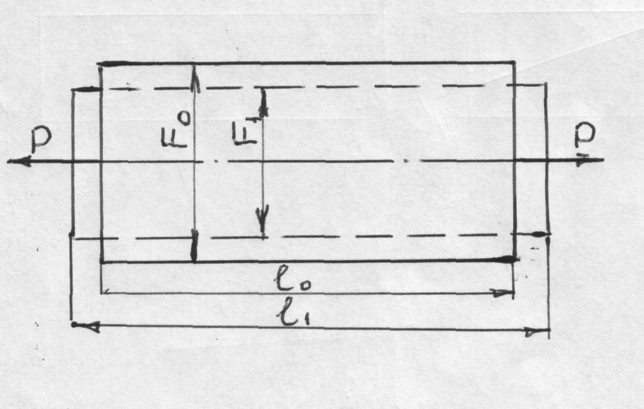
Рис. 14. Схема деформации цилиндрического стержня при одноосном растяжении

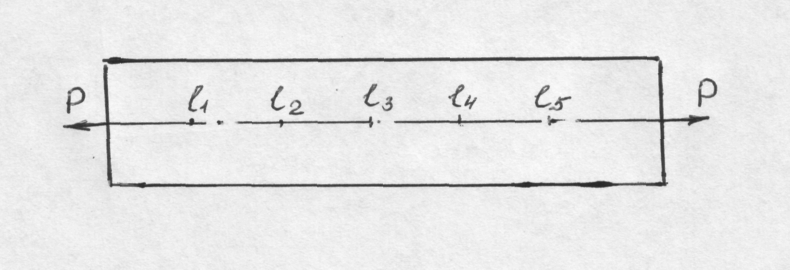
Рис. 15. Схема деформации цилиндрического стержня при одноосном растяжении для определения истинной деформации

Прологарифмируем это выражение:

, ;

Следовательно:

Истинные деформации обладают физическим смыслом, а условные не обладают. Это можно показать на конкретном примере.

Возьмем цилиндрический стержень и сдеформируем его в первом случае растяжением до двух кратной длины, а во втором сожмем в два раза и определим истинные и условные деформации.

Растяжение:

;

Сжатие:

;

Истинные деформации „е” равны по абсолютной величине и обратны по знаку, а условные деформации отличаются в 2 раза.

При уменьшении деформации приблизительно до 10% эти различия исчезают и условная и истинная деформация становятся приблизительно одинаковыми.

Кроме этого истинные деформации в отличии от условных обладают свойством аддитивности. Например, если разбить весь процесс деформации от до и от до , то при подсчете условной деформации выясниться, что суммарная деформация не равна сумме деформаций на этапах:

; ;

Что касается истинных деформаций, то суммарная истинная деформация будет равна сумме деформаций на этапах:

; ;

Свойство аддитивности истинных деформаций имеет большое практическое значение при прокатке за несколько проходов.

Для описания деформированного состояния воспользуемся описанием деформированного состояния в точке. Смещение в какой-либо точке тела в результате его деформации характеризуется вектором, соединяющим положение точки до и после деформации.

Смещения в различных точках в общем случае различны и можно говорить о векторном поле смещений в деформируемом теле. Деформация будет происходить лишь в том случае, если смещение изменяется от точки к точке. Однако деформация происходит не при любом поле смещений. При вращении смещение различных точек различно и определяется расстоянием от оси вращения. Следовательно, в случае чистого вращения переменность поля смещений от точки к точке не сопровождается деформацией.

Наличие деформации определяется:

1. Не данным полем смещения, а только изменением смещения от точки к точке (чтобы исключить поступательное перемещение тела как жесткого целого);

2. Не всем изменением поля смещений, а только той частью этого изменения, которая остается после вычета из нее вращательного перемещения тела как жесткого целого.

Например, при кручении поворачиваются оба захвата. При этом характеристикой угловой деформации является не абсолютное значение угла закручивания, а разность углов закручивания в двух сечениях образца, определенных на определенном расстоянии друг от друга.

При проведении испытаний механических свойств принято характеризовать деформации относительным изменением размеров или сечений, а также угла сдвига, то есть угла на который изменился первоначальный прямой угол, измеряемый в радианах. Относительным сдвигом называется тангенс угла сдвига, то есть g=tgα, рис.16.

Если разложить вектор смещения по координатным осям, то малые удлинения „е” и сдвиги „g” в направлении координатных осей могут быть выражены через изменения составляющих вектора смещения U, V известными соотношениями:

; ; , где

- подобно при одноосном растяжении;

- характеризует изменение прямого угла между направлениями x и y.

Для математического описания объемного деформированного состояния воспользуемся описанием деформированного состояния в точке, подобно описанию объемного напряжения.

При этом для описания деформированного состояния воспользуемся истинными удлинениями „е”, вызываемыми составляющими нормальных напряжений и сдвигами „g”, вызываемыми касательными составляющими напряжений. Принимая равномерными сдвиги вдоль координатных осей будем учитывать вдоль каждой координатной оси.

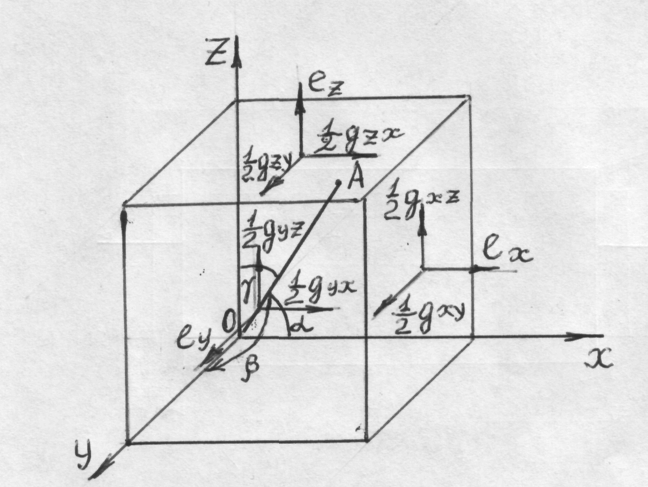
Математическое объемное деформированное состояние будет описываться полным тензором деформации, учитывающим три удлинений и шесть сдвигов, рис.17.

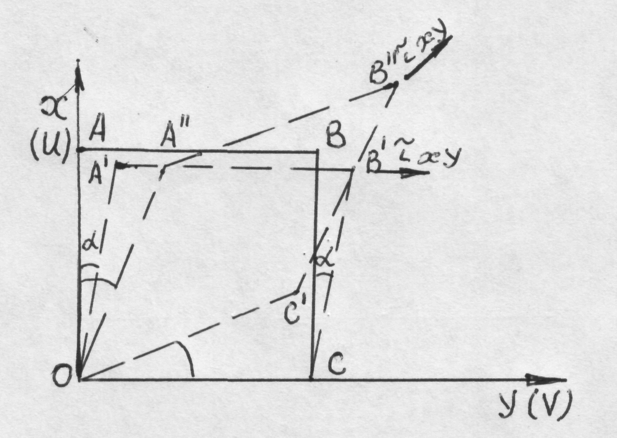Рис.16. Схема деформации при различных направлениях внешних напряжений

Р

Рис.18. Круги Мора для объемного деформированного состояния

ис.17. Схема распределения составляющих деформации при объемном деформированном состоянии

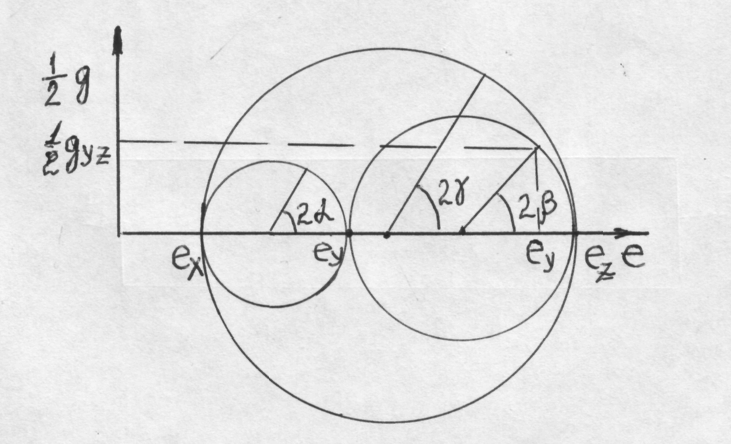
Полный тензор деформации будет иметь вид:

Если заданы три главных направления деформации, то деформированное состояние будет описываться тремя главными удлинениями – шаровым тензором деформации.

Если , то шаровой тензор деформации будет учитывать среднюю величину удлинения:

Шаровой тензор деформации учитывает изменение объема под действием внешних нагрузок. Наряду с изменением объема при деформации происходит изменение формы. Изменение формы будет описываться разностью между полным тензором и шаровым тензором деформации – девиатором деформации.

Шаровой тензор деформации описывает упругую деформацию, предшествующую пластической, и может действовать самостоятельно. Пластическая деформация без упругой невозможна, а, следовательно, девиатор деформации, описывающий пластическую деформацию, самостоятельно действовать не может.

Для описания деформированного состояния широко используется и графический метод в виде кругов Мора. Круги Мора строятся в координатах „ ”. Для построения кругов Мора необходимо знать главные истинные удлинения, которые откладываются на оси удлинений. В случае объемного деформированного состояния, зная , и определяют диаметр кругов. При > > :

; ;

Положение точки в пространстве определяется углами между вектором соединяющим выбранную точку с началом координат (ОА) и координатными осями. Найдя двойные углы, проводим радиусы векторы в каждом круге под определенным двойным углом до пересечения с кругами. Проекции точек пересечения на координатные оси позволяет определить составляющие деформации „е” и „ ”, рис.18.

Если смещение точки во всех направлениях происходит с постоянной разностью, то будем иметь однородное деформированное состояние. Обычно однородное деформированное состояние имеем при линейном растяжении гладкого стержня и при кручении стержня на поверхности одного и того же радиуса.

В большинстве случаев деформация неоднородна. В простых случаях деформированное состояние можно определить математически. При деформации тел сложной деформации деформированное состояние определяется экспериментальным путем. В области упругой деформации применяется метод тензометрирования (при малых деформациях). При пластической деформации используется метод накатных сеток. В качестве примера можно рассмотреть сжатие цилиндрического стержня, рис.19.

Учитывая то, что в месте контакта стержня с поверхностью оснастки существуют силы трения, деформация по высоте и толщине стержня будет неоднородная. Нанесение накатной сетки позволяет фиксировать эту неоднородность и путем замеров ячеек сетки оценить количественно степень деформации.