3.Напряжения и способы снижения напряженного состояния
Известно, что напряжение это приложенная нагрузка, отнесенная к единице площади поперечного сечения. Из данного определения следует, что напряжение является такой характеристикой нагрузки, которая не зависит от размеров тела к которому она приложена и имеет размерность:
сила / площадь
сечения на которую действует сила =
В единицах напряжения выражают важнейшие характеристики механических свойств (сопротивление разрушению, пластическому течению, вдавливанию, усталости, ползучести и др.).
Для определения напряжения рассмотрим случай одноосного осевого растяжения цилиндрического образца, рис.4.
В условиях
статического равновесия внешняя нагрузка
Р уравновешивается внутренней силой
сопротивления
(S – напряжение, нормальное
к плоскости сечения, F –
площадь поперечного сечения).
Исходя из схемы, условие равновесия запишется:
Р=
Для случая равномерного распределения напряжений по сечению:
=SF
и P=SF,
а
В общем случае, когда сечение стержня, к которому прикладывается нагрузка, не перпендикулярно оси цилиндра (рис.5) общее напряжение, действующее на это сечение, можно разложить на две составляющие:
1.нормальное напряжение, действующее перпендикулярно сечению – S
2.касательное,
действующее в плоскости сечения -
.
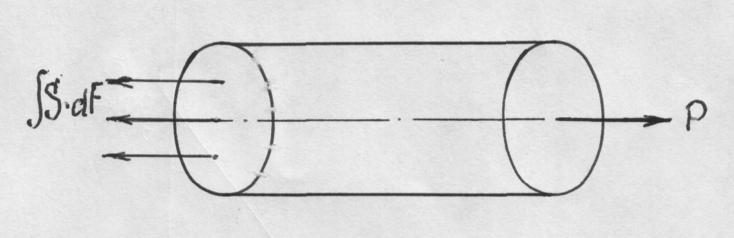
Рис.4. Схема одноосного осевого растяжения
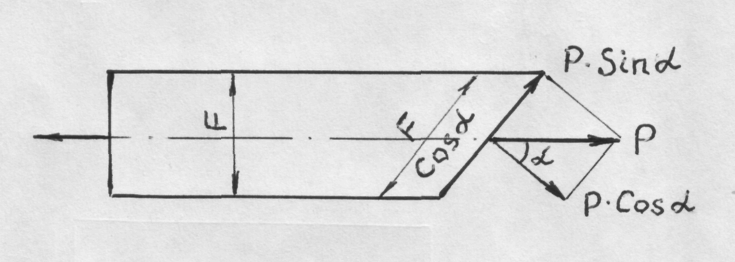
Рис.5. Схема одноосного не осевого напряжения
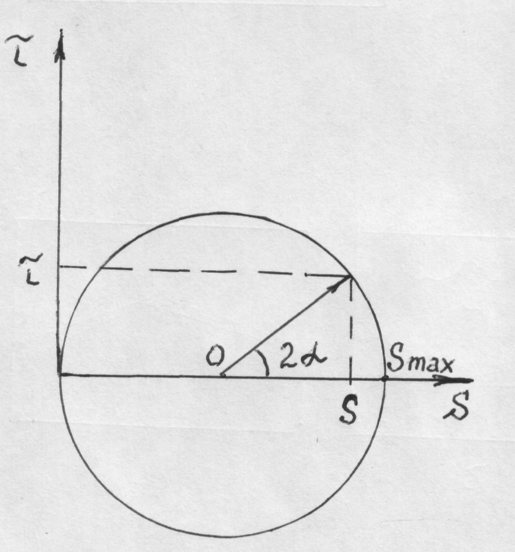
Рис.6. Круг Мора для случая одноосного растяжения
Согласно этой схемы нормальная составляющая напряжения будет равна:
а касательная составляющая напряжения будет равна:
Нормальная
составляющая напряжения будет максимальная
при α=0 и минимальная, равная 0, при α=90
.
Касательная
составляющая напряжения будет максимальная
при α=45
и равная ½
.
Для описания напряженного состояния используются различные способы:
математический (с помощью тензора напряжений)
графический (с помощью кругов Мора).
В качестве примера графического описания напряженного состояния рассмотрим построение круга Мора для случая одноосного растяжения стержня.
Преобразуем выше приведенные выражения для нормальных и касательных напряжений, приведем их к двойным углам:
Геометрическим местом точек, одновременно удовлетворяющим приведенным выражениям, будет круг радиусом ½ на оси нормальных напряжений и касающийся оси касательных напряжений, рис.6
Для определения составляющих напряжения необходимо взять угол 2α и под этим углом провести радиус вектор ОА до пересечения с кругом, найти точку А и ее проекции на координатные оси.
Более сложным напряженным состоянием является двухосное и трехосное напряженное состояние.
Примером двухосного напряженного состояния может служить случай одновременного действия сжимающих и растягивающих напряжений, рис.7.
Для описания
такого напряженного состояния графически
с помощью кругов Мора необходимо
представить его в виде двух более простых
напряженных состояний. Для этого прибавим
и вычтем величину напряжений
из
.
В результате получим два более простых
напряженных состояния: одно из них будет
представлять собой одноосное растяжение
с напряжением
+
,
другое – двухосное сжатие с напряжением
,
рис.7.
Такое
сложное напряженное состояние будет
описываться кругом Мора радиусом
,
рис. 8.
Описание объемного напряженного состояния
Одноосное и двухосное напряженное состояние в реальных условиях встречаются очень редко. Самым распространенным напряженным состоянием является объемное напряженное состояние.
Для описания объемного напряженного состояния необходимо разложить напряжения по трем направлениям. В практике прибегают к описанию напряженного состояния в точке. Для этого необходимо точку поместить в систему координат и вокруг точки описать прямоугольный параллелепипед. Это позволяет вынести составляющие касательных и нормальных составляющих напряжений на три грани параллелепипеда, рис.9.
Каждое из напряжений, действующих на каждую грань может быть разложено на одну нормальную составляющую с индексом координатной оси и 2 касательные с первым индексом нормальной составляющей и вторым индексом координатной оси совпадающим по направлению с касательной составляющей.
Для
произвольно выбранной точки напряженное
состояние будет описываться девятью
составляющими, три из которых будут
составляющими нормальных напряжений
и 6 – касательных составляющих (
,
,
,
,
,
,
,
,
).
Математически напряженное состояние может быть описано тензором напряжений:
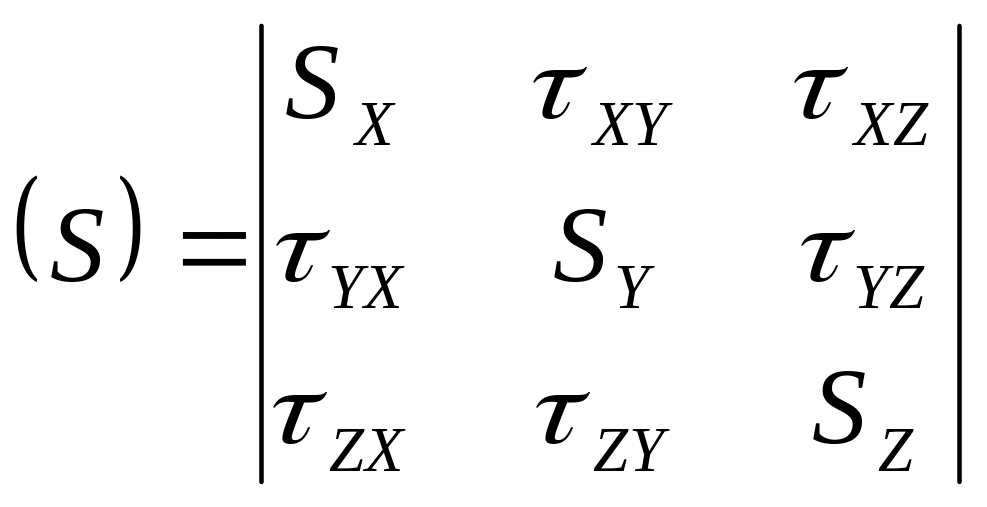
Исходя
из соображений, что суммарный вращающий
момент относительно любой оси равен 0,
,
=
,
=
.
В этом случае число составляющих
напряжений уменьшается до 6.
Если система координат выбрана таким образом, что на площадках перпендикулярных к осям действовали бы только нормальные напряжения, то напряженное состояние будет описываться только нормальными напряжениями и тензор напряжения примет вид:
Такие напряжения называются главными, а тензор – шаровым тензором напряжений. Если известно положение точки в пространстве, определяемое направляющими косинусами, и главные напряжения, то представляется возможным определение нормальных и касательных напряжений к заданной площадке:
Доказано, что максимальные касательные напряжения действуют на площадках по углам 45 к главным осям и определяются по полуразности соответствующих главных нормальных напряжений
.
Если на тело действует только нормальные напряжения, то напряженное состояние описывается шаровым тензором, который вызывает изменение объема без изменения формы.
Если на тело действуют нормальные и касательные напряжения, то напряженное состояние описывается полным тензором напряжений и вызывает изменение и объема и формы.
Напряженное состояние вызываемое изменение формы определяется девиатором напряжений, который определяется по разности между полным и шаровым тензором напряжений.
Д=(S)
– (
),
где:
=
Д=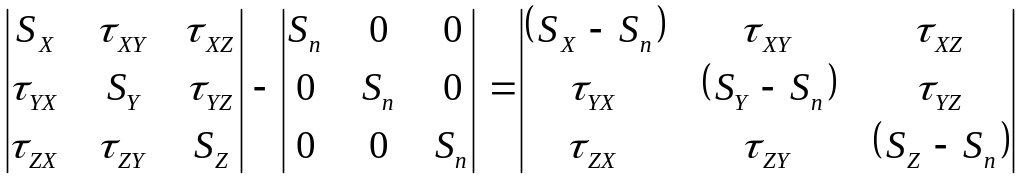
Изменение объема без изменения формы возможно лишь в случае гидростатического растяжения или сжатия при условии что все напряжения действующие в различных направлениях равны. Это возможно в случае действия шарового тензора, которой вызывает упругую деформацию. Упругая деформация всегда предшествует пластической деформации, а, следовательно, шаровой тензор напряжений может существовать самостоятельно.
Изменение формы без изменения объема могут вызывать касательные напряжения и напряженное состояние описывается девиатором напряжений.
Девиатор напряжений действовать самостоятельно не может, так как пластическая деформация без упругой существовать не может.
Наряду с математическим описанием объемного напряженного состояния широко используется графический с помощью кругов Мора.
Для построения кругов Мора необходимо знать значения нормальных составляющих напряжений , и . Необходимо выбрать систему координат τ – S. Примем < < и отложим эти напряжения на оси S, рис.10.
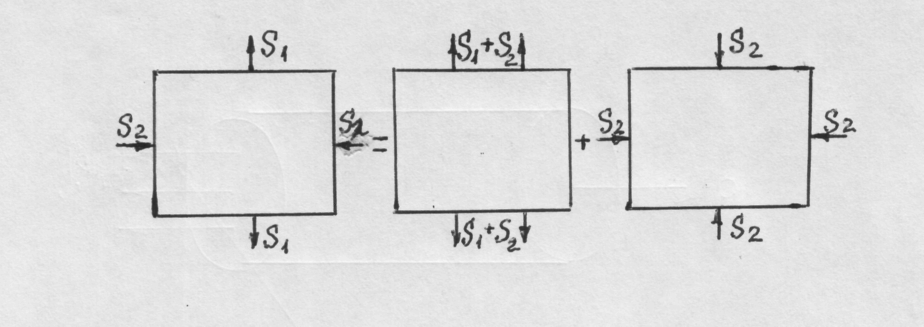
Рис. 7. Схема двухосного напряженного состояния
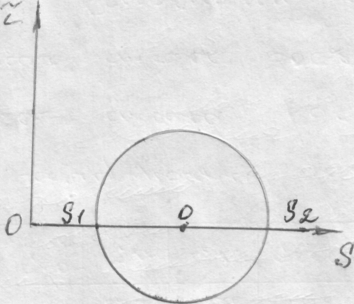
Рис. 8. Круг Мора для случая двухосного напряженного состояния
Рис. 9. Схема напряженного состояния в точке
Для каждого из
трех направлений строим круги Мора. Для
направления xy диаметр
круга Мора будет определяться разностью
между главными напряжениями
,
то есть центр круга Мора будет находиться
между
и
.
Для направления
и для направления
.
Зная положение точки А в пространстве, определяемое углами между вектором ОА и каждой из координатных осей представляется возможным определить касательные и нормальные составляющие напряжений. Для этого необходимо из центров кругов провести радиусы векторы под углами 2α, 2β, 2γ до пересечения с кругами. Проекции точек пересечения на координатные оси позволит определить нормальные и касательные составляющие напряжений.