9.3. Модельный метод изучения деформации полимера

Что касается вопроса механизма деформации полимерных материалов, то он изучен недостаточно, хотя сам факт сочетания высокополимерами упругих и вязких свойств известен давно со времен Максвелла, предложившего модель вязкоупругого поведения полимерных материалов. Суть этой модели заключается в том, что она включает последовательное соединения идеально упругой пружины и демпфера (тела нагруженного в вязкую жидкость), рис.65. При быстром нагружении полимерных материалов они оказываются малодеформируемыми и стремятся упруго восстановить свою форму. Их механическое противодействие прямопропорционально деформации (закон Гука) пружины в модели Максвелла. При медленном нагружении полимерные тела текут, при этом скорость деформации должна быть прямопропорциональна прикладываемому напряжению. Течение материала в модели учитывается течением жидкости в демпфере, подчиняющиеся закону Ньютона. Согласно этой модели, сразу после приложения нагрузки наступает упругая деформация пружины, а затем в течение всего действия нагрузки будет развиваться необратимая часть деформации, учитываемая вязким течением жидкости в демпфере.

Общая деформация в каждый момент времени будет складываться из:

, где:

- упругая деформация пружины;

- деформация вязкого элемента.

Упругая деформация возникает мгновенно и её скорость будет определяться скоростью приложения напряжения:

Учитывая то, что упругий и вязкий элементы соединены последовательно, величина напряжения на них будет одинакова. При увеличении нагрузки, пропорционально возрастает скорость течения жидкости:

σ = ηυ, где:

η – вязкость жидкости в демпфере.

Учитывая то, что υ= закон Ньютона запишется в виде:

,

а общая деформация запишется в виде:

.

Данное дифференциальное уравнение является простейшей моделью вязкоупругого поведения полимерных материалов.

Рассмотрим пример линейного полимера.

Пусть , тогда .

Это справедливо, когда в материале протекают релаксационные процессы напряжений при сохранении постоянного удлинения.

Если проинтегрировать приведенное выражение от 0 до t и от до , то получим:

.

Обозначим через - время релаксации напряжений.

Тогда:

При τ=t

При очень медленном нагружении t >>τ и

При резком приложении нагрузки t << τ величина t /τ → 0 и , т.е. релаксация напряжений не успевает пройти.

При σ = const и тогда:

,

что является одной из форм закона Ньютона.

В полимерах под действием постоянного напряжения происходит вязкое течение за всё время действия напряжения.

Рассмотренная модель Максвелла не учитывает упругости отличной от Гуковской, возникающей за счет закручивания молекул. Раскручивание молекул можно представить как деформацию пружины в вязкой среде. Это учтено в модели Кельвина – Фогта представленной параллельным соединением упругого и вязкого элементов, рис.66. Если принять жидкость несжимаемой, то мгновенное нагружение не вызывает в вязком элементе никакой деформации. Упругая деформация станет возможной через определенное время, необходимое для соответствующего перемещения демпфера.

Рис.65. Схема Максвелла

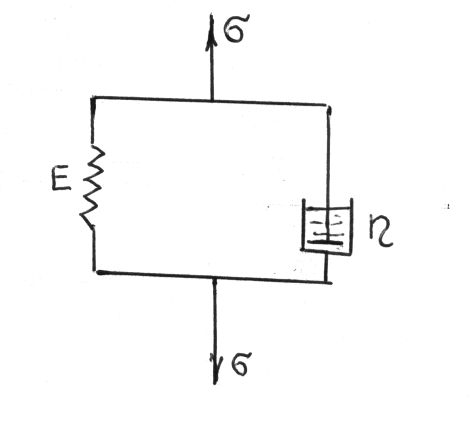
Рис.66. Модель Кельвина-Фогта

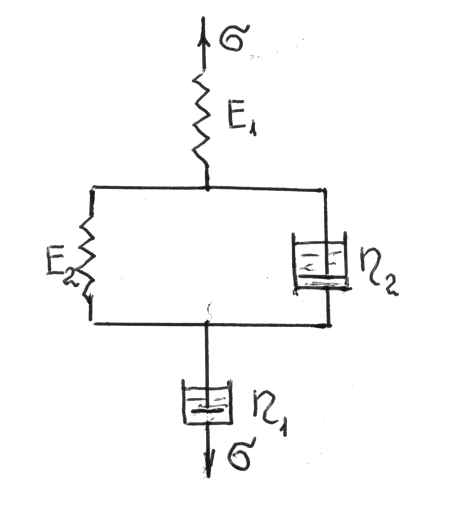
Рис.67. Объединенная модель деформации

В отличие от модели Максвелла величина удлинения будет одинакова для обоих элементов, а напряжение будет складываться из напряжений, возникающих в каждом из элементов.

Учитывая то, что , а дифференциальное уравнение деформации будет иметь вид:

Полученное уравнение легко интегрировать в пределах времени от 0 до t, введя промежуточную переменную .

Обозначив , получим интегральное уравнение деформации:

Умножив дифференциальное уравнение деформации на t и разделив на получим:

.

Если t << τ, слагаемые можно пренебречь, тогда после сокращения на t, получим закон Ньютона:

Если t >> τ, то в интегральном уравнении деформации член обращается в нуль и уравнение примет вид закона Гука:

Таким образом, деформация по модели Кельвина – Фогта за малый промежуток времени будет определяться величиной смещения поршня в демпфере. Какую бы большую нагрузку не приложили упругая деформация не разовьется раньше, чем разовьется пластическая деформация в демпфере и общая деформация будет определяться скоростью вязкого течения.

При длительном действии нагрузки, деформация вязкого течения успеет развиться полностью и процесс деформации закончится тогда, когда действующая сила уравновесится модулем упругости пружины.

Величина общей деформации будет определяться законом Гука.

Практика работы с полимерами показала, что в действительности общая деформация полимеров складывается из истинно упругой деформации, подчиняющейся закону Гука (моделируемой упругой пружиной), из необратимой деформации (моделируемой вязким элементом – демпфером) и, наконец, упругой развивающейся во времени или высокоэластической деформации (моделируемой элементом Кельвина – Фогта), рис.67. Изменение состояния этой модели при нагружении и последующей разгрузке можно представить в виде графика, рис.68.

Как только к объединённой модели будет приложена нагрузка, мгновенно произойдет деформирование упругого элемента Е1 на величину деформации, определяемой модулем пружины. После начала деформации через время t1 величина упругой деформации достигнет величины АВ = , рис.68. Далее с течением времени будет происходить деформация вязкого элемента с вязкостью среды η1, а также начнётся упругая деформация пружины с модели Е2, причём этот процесс будет тормозиться медленным течением в вязком элементе η2. К моменту времени точки С развитие упругой деформации пружины Е2 полностью закончится и далее будет наблюдаться вязкое течение, выражающиеся прямолинейным участием СД вплоть до снятия нагрузки в точке Д.

Для вычисления величин вязкой и эластической деформации воспользуемся следующим приёмом. С момента начала деформации (в точке В) вязкое течение происходило всё время с постоянной скоростью, определяемой наклоном участка СД. Экстраполируем этот участок к оси AL, соответствующей началу деформации. Тогда величина деформации вязкого течения к моменту окончания высокоэластической деформации (точка С) окажется равной СС'. Кривая BC' показывает ход развития высокоэластической деформации. Отрезок BL представляет собой величину эластической деформации, которая определяется величиной упругой деформации пружины с модулем Е2, т.е. . Окончание деформации вязкого течения произойдет в момент снятия нагрузки. Величина деформации в этот момент определяется отрезком ДМ, согласно закону Ньютона:

, где:

(t1 – t2) – время действия нагрузки.

Как только прекратится действие нагрузки, исчезнет упругая деформация ДF = AB и на участке FK будет происходить заторможенное сокращение пружины с модулем Е2, т.е. исчезновение высокоэластической деформации.

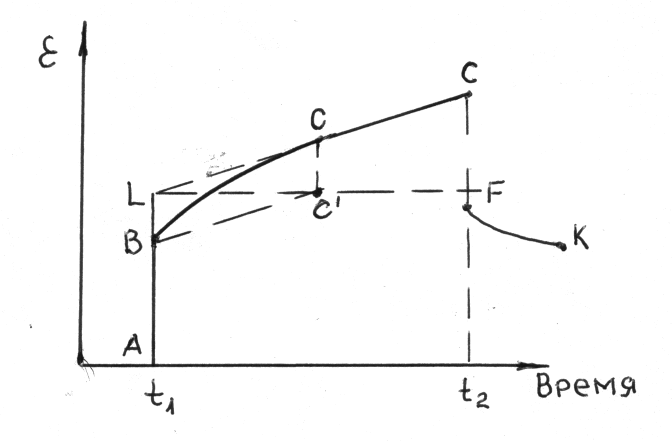
Рис.68. График зависимости деформации от времени

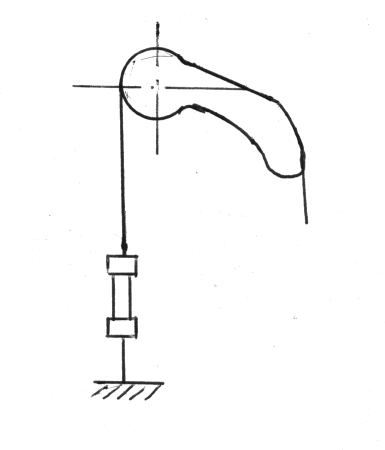
Рис.69. Схема приспособления, обеспечивающая постоянство напряжения при испытании

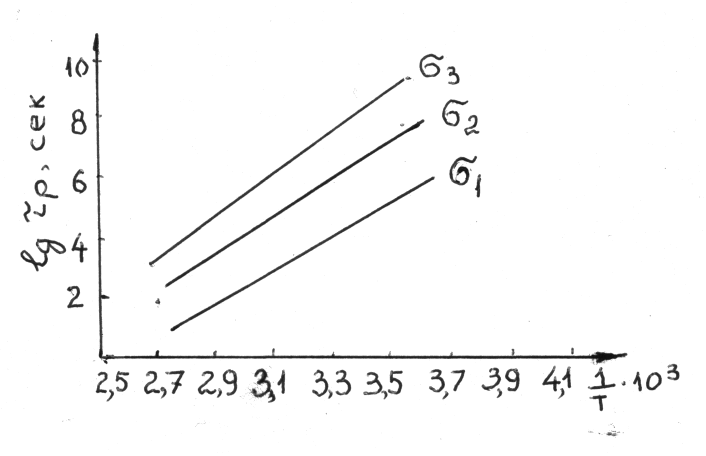
Рис.70. Зависимость lgτ_р= при различных величинах напряжений для полистирола

Точка К соответствует моменту окончания сокращения деформации. Ордината точки К определяется величиной деформации вязкого течения, а, следовательно, эта ордината будет равна отрезку ДМ.

В течение всего периода действия силы общая деформация будет складываться из трех составляющих:

, где:

t – время деформации; τ – время релаксации в элементе Кельвина – Фогта.