1. Зарождение трещины;

2. Развитие трещины.

Первая стадия связана с пластической деформацией. Вторая стадия – развитие трещины при хрупком разрушении протекает без признаков пластической деформации.

Характерной особенностью хрупкого разрушения является малая пластическая деформация, близкая к предельной упругой деформации, и большая скорость разрушения, что представляет большую опасность.

Нанесение надреза на поверхность вызывает концентрацию напряжения у дна надрезов, понижает пластичность и повышает прочность, то есть величину напряжений, при которой наступает разрушение без внешних признаков пластической деформации.

Для определения величины напряжении, развивающихся у вершины трещины, воспользуемся следующей схемой, рис.48.

Согласно Ирвину, максимальная величина напряжений – σ_max у вершины элептической трещины длиной 2а с радиусом скругления r может быть определена из уравнения:

, где:

σ – внешнее прикладываемое напряжение.

В идеально хрупком теле даже при сравнительно малом внешнем напряжении напряжение у вершины может на столько повышаться, что превзойдет теоретическую прочность и приведет к разрыву межатомных связей и разрушению.

При этом выделяется упругая энергия, но затрачивается работа на создание новой поверхности трещины. В случае приложения напряжений к тонкой пластины единичной ширины, содержащей центральную или поверхностную трещину, выделяющаяся упругая энергия будет равна:

Поверхностная энергия, затрачиваемая на образование новых поверхностей будет равна:

, где:

- удельная поверхностная энергия.

Гриффитс постулировал, что трещина начинает продвигаться нестабильно, когда малое приращение ее длины перестает изменять общую энергию системы, то есть

,

Откуда:

Если образовалась трещина критической длины 2а, ее дальнейшее развитие будет проходить при более низком напряжении, так как величина напряжения обратнопропорциональна длине трещины.

У абсолютно хрупких тел, таких как стекло, критический размер трещины, согласно критерию Гриффитса, составляет всего несколько микрон. Подтверждением доминирующей роли таких трещин является тот факт, что прочность стеклянных нитей, не содержащих поверхностных дефектов, приближается к теоретической прочности. Попытки приложения критерия Гриффитса к металлам не дали успеха.

В металлах для зарождения трещины необходима пластическая деформация. С другой стороны, пластическая деформация, сопровождающая рост трещины, стремится притупить трещину, а, следовательно, величина энергии на ее развитие должна возрастать. С целью учета влияния пластической деформации, следы которой обнаружены экспериментально при самом хрупком разрушении, Орован предложил видоизменить формулу

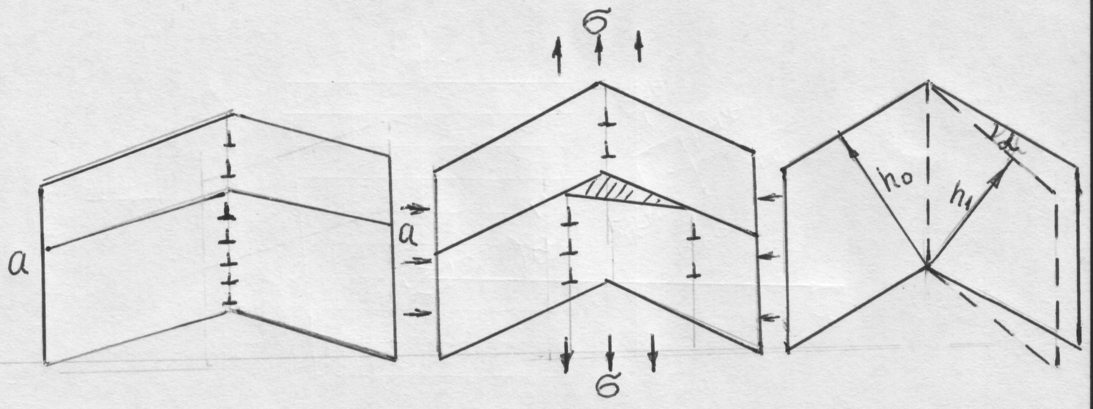
Рис. 47. Схема зарождения трещины при пересечении с дислокационной границей наклона

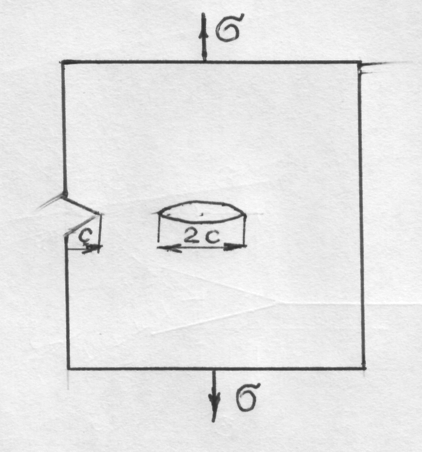
Рис. 48. Схема концетратора напряжений

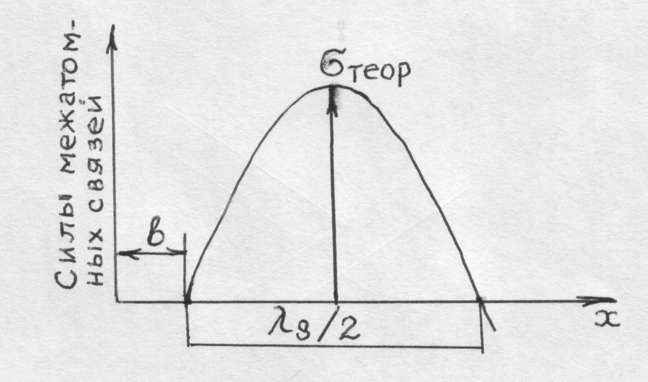
Рис. 49. Зависимость сил межатомного взаимодействия между атомами

Гриффитса, вводя в нее вместо поверхностной энергии величину энергии пластической деформации

Для большинства металлов .

В общем виде связь между и выведена Гилманом:

, где:

G – модуль сдвига

σ_т – предел текучести.

Рассмотрим хрупкое разрушение с позицией атомнокристаллического строения металлов. Принимаем, что в металлах нет дефектов и что деформация вплоть до разрушения чисто упругая. Вернемся к схеме, уже используемой для расчета теоретической прочности, рис.49.

Принимая закон изменения сил межатомного взаимодействия при их смещении из положения равновесия близким к синусоидальному, можно записать:

, где:

х – величина смещения атомов

λ_S – длина волны

b – исходное расстояние между атомами.

Для малых величин смещений

Для малых упругих деформаций

, где:

- относительная деформация.

Приравнивая правые части уравнений, получим:

*

Работа затраченная внешними силами расходуется на разрушение:

то есть на образование двух поверхностей разрушения, обладающих удельной поверхностной энергией γ_S

, откуда:

Определив λ_S и подставив в уравнение *, получим:

Приняв , получим: .

В практике, как было указано выше, никогда не достигается теоретическая прочность. Низкая прочность хрупких тел связана с различными дефектами (трещинами, надрезами и др.). наличие острого надреза или трещины приводит к увеличению приложенного напряжения до на расстоянии порядка а от вершины трещины с радиусом R, рис.50.

Если это напряжение достигнет величины теоретической прочности, трещина будет развиваться, что приведет к разрушению.

Приравнивая значение напряжения у вершины трещины теоретической прочности, получим:

Из этого уравнения величина напряжения, соответствующая началу развития трещины, будет равна:

Если принять нижним пределом расстояния от вершины трещины параметр решетки „b” и длину надреза а=10⁴b, то: .

Это означает, что если в теле присутствует трещина длиной 10^-4 см, то напряжение разрушения снижается в сотни раз по сравнению с теоретической прочностью.