7.3. Влияние различных факторов на эффект деформационного упрочнения
Среди факторов, оказывающих влияние на эффект деформационного упрочнения следует назвать:
температуру;
химический состав и структуру;
скорость деформации.
7.3.1. Влияние температуры на эффект деформационного упрочнения
Для анализа влияния температуры на величину деформационного упрочнения воспользуемся кривыми напряжение деформация для металлов с ГЦК решеткой на примере меди, рис.39. согласно этому рисунку при высоких температурах кривые имеют примерно параболическую форму, кривая 4. при пониженных температурах, ниже комнатной, кривые 1, 2, отмечается четко выраженный участок легкого скольжения (I стадия). При этом следует отметить что I стадия деформационного упрочнения зависит не только от температуры. Она существенно зависит от природы металла и его чистоты.
Что касается II стадии деформационного упрочнения – множественного скольжения, то эффект упрочнения слабо зависит от температуры.
На заключительной III стадии повышение температуры будет сопровождаться уменьшением величины эффекта упрочнения.
Применительно к поликристаллическим материалам Якотовичем М.В. и Павловым В.А. Предложено разделять диаграммы растяжения на два типа, рис.40.
низкотемпературный (кривая 1), когда максимум усилия наблюдается в конце кривой;
высокотемпературный (кривая 2), когда максимум усилия наблюдается в начале диаграммы.
Резкий спад в конце диаграммы связан с образованием шейки, предшествующей разрушению.
7.3.2. Влияние химического состава на эффект деформационного упрочнения
Влияние химического состава на эффект деформационного старения следует рассматривать с позиций взаимодействия элементов, входящих в состав сплава, с дефектами кристаллического строения. При малых концентрациях элементов, играющих роль примесей, необходимо рассматривать их влияние с позиций их влияния на подвижность дислокаций. В этом случае примесные атомы взаимодействуют с дислокациями образуя атмосферы Коттрелла, Сузуки, Снука. Примесные атомы внедрения, такие
к
Рис.40. Диаграммы
растяжения поликристаллического кадмия
Атмосферы Коттрелла атомами внедрения в основном образуются в металлах с ОЦК решеткой при малых концентрациях (10-3÷10-2%). Атмосферы Сузуки присущи в основном металлам с ГЦК решеткой. При этом атомы замещения с радиусом меньше радиуса атомов матрицы скапливаются в сжатой области кристаллической решетки над дислокацией, а атомы замещения с радиусом больше радиуса атомов матрицы в растянутой области кристаллической решетки под дислокацией. Упругое взаимодействие между атомами примесей и краевыми дислокациями снижает энергию деформации дислокаций и делает ее более стабильной.
В металлах с ОЦК решеткой примесные атомы внедрения занимают позицию в центрах граней куба и по ребрам. При этом внедрение атомов приводит к тетрагональным искажениям решетки и увеличению сдвиговых и гидростатических напряжений. Все это уменьшает подвижность дислокаций.
Рис. 38. Схема образования порогов на пересекающихся дислокациях
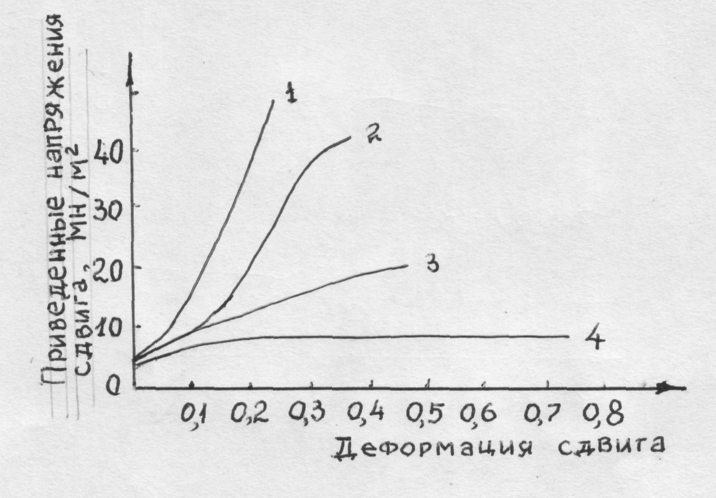
Рис.39. Кривая напряжение-деформация для меди при различных температурах: 1 – 4,2 К; 2 – 77 К; 3 – комнатная температура; 4 – 600 К
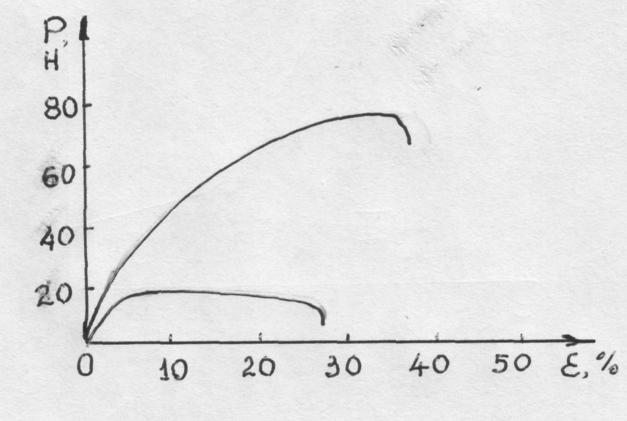
Рис.40. Диаграммы растяжения поликристаллического кадмия
В металлах с ГЦК решеткой примесные атомы вызывают симметричные искажения кристаллической решетки и эффект блокировки дислокаций будет слабее чем в металлах с ОЦК.
Притяжение растворенных атомов к дислокациям объясняется электростатическим взаимодействием ядра дислокации с дополнительным зарядом, который возникает у инородного атома с атомами растворителя. Величина этого заряда будет больше, чем больше разница в валентности атомов растворителя и растворенного вещества.
Легирующие элементы находясь в твердом растворе, по разному влияют на его стабильность. Пластическая деформация под действием внешних нагрузок может вызывать или стимулировать протекание многих фазовых изменений (полиморфных, распад твердых растворов, изменять степень порядка и др.) связанных бездиффузионными и диффузионными перемещениями атомов. В то же время вызванные сдвигами при пластической деформации диффузионные процессы оказывают влияние на дальнейшее развитие пластической деформации. Это должно вызывать аномальный ход кривых напряжение – деформация, особенно проявляющиеся при деформации метастабильных твердых растворов, для осуществления внутренних изменений которых нужны небольшие диффузионные перемещения. Примером может служить сплав Zn – 20% Al, имеющий мелко зернистую глобулярную структуру (количество мелких равноосных частиц второй фазы ~50%). В процессе деформации резко падает прочность и повышается пластичность (удлинение может достигать сотен процентов). В этих сплавах под действием деформации происходят направленные процессы диффузии, способствующие залечиванию образующихся в результате межзеренного скольжения пор. Если же этот сплав подвергнуть предварительно стабилизирующему отжигу, явление сверхпластичности при деформации не проявляется.
В ряде случаев, когда диффузионные процессы при деформации метастабильных твердых растворов имеет направленный характер, происходит упрочнение сплава. Объясняется это тем что в процессе деформации происходят начальные стадии старения с образованием новых фаз.
В случае стабильного состояния твердого раствора упрочнение при деформации не наблюдается, так как отсутствуют процессы распада твердого раствора под действием пластической деформации. Примером могут служить стали со стабильным и метастабильным аустенитом. В случае сталей с метастабильным аустенитом в процессе деформации аустенит превращается в мартенсит деформации и стали упрочняются.
При концентрации легирующих элементов сверх предела растворимости в структуре происходит выделение избыточной фазы, которая будет оказывать существенное влияние на сопротивление деформации и эффект упрочнения. Эффект деформационного упрочнения в этом случае будет зависеть от природы выделяющихся фаз (когерентности связи с матрицей), количества, размеров и характера их распределения в матрице. Любые выделения являются препятствием движению дислокаций, а, следовательно, будут приводить к повышению эффекта деформационного упрочнения. При небольшом количестве выделений расстояние между ними большое искажение будет проходить путем изгиба петель дислокаций между ними, ри.41.
Минимальный радиус кривизны, на который должна изогнуться дислокация, составляет величину между х/4 и х/2, где х – расстояние между частицами. Величина напряжения, необходимого для того, чтобы протолкнуть дислокации между частицами будет равна:
,
где:
G – модуль сдвига
b – вектор Бюргерса
х – расстояние между частицами.
Это связь хорошо согласуется для сталей, сплавов Al – Cu, Cu – Cr и др. Наглядное представление дают данные полученные на сплаве Al – 2% Cu, рис.42.
Наибольшая
величина напряжений наблюдается в
случае расстояния между частицами
.
Наименьшая величина напряжений
соответствует перестаренному состоянию,
кривая 3.
Приведенные данные не учитывают концентрацию меди в данном растворе. При выделении частиц концентрация меди в твердом растворе понижается, а, следовательно, сопротивление сдвигу в твердом растворе будет меняться. С повышением концентрации меди в твердом растворе будет возрастать сопротивление сдвигу.
Следовательно, можно сопоставлять, с определенной погрешностью, лишь кривые 2 и 3.
При очень малых расстояниях между частицами дислокация не может пройти между ними. В этом случае скольжение скорее всего пройдет через эти частицы. Наряду с этим может существовать интервал расстояний между частицами, при котором происходит поперечное скольжение и скольжение огибает частицы, таким образом, с помощью поперечного скольжения можно избежать скольжение сквозь частицы.
Важное значение имеет фактор формы выделяющихся частиц. Здесь могут существовать два эффекта. Один из них – то, что количество плоскостей скольжения пересекаемых при выделении частиц, занимающих данную часть объема, зависит от формы этих частиц. Оно является наименьшим для сферических частиц, более высоким для частиц в форме пластин и еще более высоким для выделений в форме стержней. Исходя из этого меняется число плоскостей скольжения, в которых расположены препятствия скольжению дислокаций. Максимальный эффект упрочнения будет обеспечиваться волокнистыми выделениями. Подтверждением этому служат волокнистые композиционные материалы.