6. Равновесие жидкости

Законы равновесия жидкостей изучает раздел гидравлики - гидростатика. Для покоящейся жидкости, находящейся в поле тяжести Земли, уравнение Эйлера (4.5) перепишется в виде

. (6.1)

Это уравнение равновесия жидкости в общем виде, описывающее закон распределения гидростатического давления. Перепишем ее в проекциях на оси координат, направляя ось z вертикально вверх:

. (6.2)

Если плотность жидкости считать постоянной во всем ее объеме, то уравнение (6.2) непосредственно интегрируется:

. (6.3)

Переписав это уравнение в виде

, (6.4)

получим основное уравнение гидростатики, определяющее гидростатический закон распределения давления в однородной несжимаемой жидкости, покоящейся в поле тяжести Земли. Для двух точек одного и того же объема покоящейся жидкости уравнение (6.4) представляется в виде

. (6.5)

Поверхность, во всех точках которой давление одинаково, называется поверхностью равного давления. Если единственной массовой силой является сила тяжести, то поверхности равного давления представляют собой семейство горизонтальных плоскостей. Действи-тельно, из (6.2) при p=const получим dz=0 или z=const. То есть каждому значению z соответствует плоскость, в каждой точке которой давление имеет одинаковое значение. Поверхность, граничащая с газовой средой, называется свободной поверхностью. В данном случае она является одной из плоскостей равного давления.

П

Рис.6.1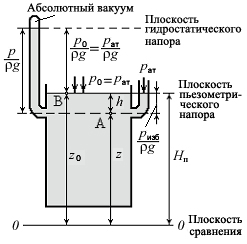

рименим основное уравнение гидростатики к точкам А и В, расположенным на глубине h и свободной поверхности соответственно (рис.6.1). Давление на свободной поверхности обозначим p₀, его называют внешним давлением. Оно может быть равным атмосферному (p₀= p_ат), большим (p₀ > p_ат) или меньшим (p₀ < p_ат) атмосферного. Из основного уравнения гидростатики имеем

. (6.6)

Отсюда

, (6.7)

где z₀–z=h. Тогда

. (6.8)

Величину gh называют весовым давлением, так как она равна весу столба жидкости при единичной площади и высоте h. Давление p иногда называют абсолютным давлением.

Избыточным давлением называют разность

. (6.9)

В гидротехнических сооружениях, как правило, на свободной поверхности давление равно атмосферному, в этом случае избыточное и весовое давления совпадают.

Если давление в жидкости меньше атмосферного, то имеет место вакууметрическое давление

. (6.10)

Закон распределения в жидкости гидростатического давления графически представляют в виде эпюр давления (рис.6.2). Они изображаются векторами, их направления и длины соответствуют направлениям и значениям давлений.

Е

Рис.6.2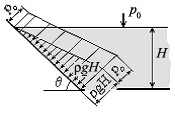

сли свободная поверхность открыта в атмосферу (p₀=p_ат), то сила избыточного давления на горизонтальную площадку площадью на глубине h определяется по формуле

. (6.11)

Если налить жидкость в сосуды различной формы, то из этой формулы очевидно, что при равенстве p₀, плотностей , площадей основания  и глубин h сила давления на горизонтальное дно будет одной и той же. Этот факт получил название гидростатического парадокса.

Из основного уравнения гидростатики вытекает закон Паскаля: изменение давления в любой точке покоящейся жидкости передается в остальные ее точки без изменений. Действительно, если изменить в одной точке давление на p₁, не нарушая равновесия жидкости, то во второй жидкости давление должно измениться на величину p₂. Т.е.

. (6.12)

О

Рис.6.3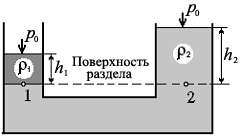

тсюда следует, что p₁=p₂.

Пусть имеется два открытых сообщающихся сосуда, содержащих жидкости с различными плотностями _и _рис.6.3). Внешнее давление на их свободных поверхностях одинаково. Поверхность раздела жидкостей является поверхностью равного давления, представляющую собой горизонтальную плоскость. Следовательно, _gh₁ _gh₂. Тогда

. (6.13)

То есть, в этом случае высоты уровней над плоскостью раздела жидкостей будут обратно пропорциональны плотностям жидкостей.

Пример 6.1. Определить полное гидростатическое давление на дно открытого прямоугольного сосуда, а также силу давления на дно. Сосуд наполнен ртутью (γ = 133 416 Н/м³). Глубина наполнения h=0,8 м. Дно сосуда имеет следующие размеры: a=0,6 м и b=0,4 м.

Решение. Гидростатическое давление в точке определяется по формуле (6.8). Так как данном случае p₀ = р_ат, то

Давление на дно сосуда будет

р= 9,8110⁴ + 133 4160,8=204832,8 Н/м²

Сила давления на горизонтальную поверхность определяется по формуле , где  – площадь дна сосуда.

Таким образом, p_полн = 49159,87 Н.

Пример 6.2. Определить высоту, на которую поднимается масло в вакуумметре (рис.6.4), если абсолютное давление внутри баллона р_вак=90 252 Н/м².

Р

Рис.6.4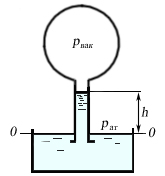

ешение. Составим уравнение равновесия, относительно горизонтальной плоскости 0-0.

Гидростатические давления, действующие изнутри и с внешней стороны , будут равны, так как система находится в равновесии. Поэтому

.

Подставляем численные значения и получаем

h= (98100-90252) : 7357,5 = 1,07 м.

П

Рис.6.5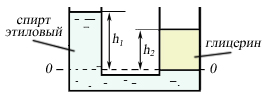

ример 6.3. На рисунке 6.5 представлена система сообщающихся сосудов. В левом сосуде налит спирт этиловый (ρ₁ = 790 кг/м³), а в правом- глицерин (ρ₂ = 1250 кг/м³). Определить на какой высоте h₂ установится уровень в сосуде с глицерином, если в левом сосуде уровень спирта выше линии раздела на h₁= 85см.

Решение. Из закона сообщающихся сосудов следует

= = 0,54 м.

Рис.6.6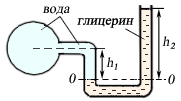

Пример 6.4. Определить высоту h₁, если давление воды внутри левого баллона р₀ = 105 кН/м², а высота h₂ равна 95 см. Внутри левого баллона и в трубке – вода, а в правой – глицерин.

Решение. Определим плоскость сравнения через границу раздела жидкости. Составим уравнение равновесия относительно этой плоскости.

,

отсюда

= = 0,48 м.

Контрольные вопросы.

1. Каковы особенности напряженного состояния покоящейся жидкости?

2. Каковы основные отличительные свойства нормального напряжения поверхностных сил в покоящейся жидкости?

3. Гидростатическое давление – векторная или скалярная величина?

4. В каких единицах измеряется давление? Чему равно атмосферное давление?

5. Что такое абсолютное, весовое, избыточное, вакуумметрическое давление?

6. Есть ли различие в понятиях «гидростатический напор» и «пьезометрический напор»? Если есть, то в чем их различие?

7. Может ли движущаяся жидкость находиться в равновесии? Если может, при каких условиях?