Расход потока не меняется, если на пути фильтрации он не теряет и не приобретает воду. Для этого необходимо, чтобы границы, ограничивающие его снизу, сверху и сбоков были непроницаемы. Эти условия, как правило, не соблюдаются, и расход потока на пути фильтрации меняет свои значения. Особенно большую роль играет водообмен подземных вод через зону аэрации, а именно, инфильтрация, конденсация и испарение влаги на свободной поверхности грунтовых вод. На рис. 11.7. представлен случай линейный фильтрационный поток с п

Рис.7. Расчетная схема линейного потока безнапорных

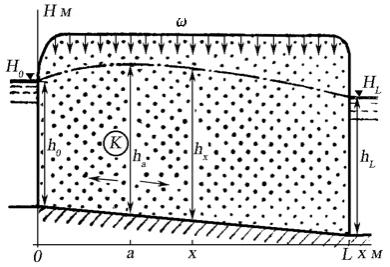
Подземных вод с инфильтрационным питанием

еременным расходом.

Интенсивность этого водообмена на единице площади поверхности грунтовых вод за единицу времени называется инфильтрационным питанием.

Вследствие инфильтрационного питания расход потока подземных вод меняется согласно линейной функции

, (11.62)

где q_x - расход на расстоянии х, м²/сут; q₀ - расход при х=0, м²/сут;  - инфильтрационное питание, м/сут.

Согласно закону Дарси

. (11.63)

Решим систему этих двух уравнений относительно q₀:

. (11.64)

Примем среднее значение h_x в интервале от Н₀ до Н_х величиной постоянной и равной (h₀+h_x)/2. Тогда

(11.65)

Это уравнение должно быть справедливо и при x=L, h_x=h_L и H_x=H_L. Поэтому

(11.66)

Отсюда следует, что

(11.67)

При горизонтальном водоупорном ложе (i=0)

(11.68)

Таким образом, при наличии фильтрационного питания величина единичного расхода не постоянна, а является функцией х. Сечение, в котором единичный расход равен 0, называется водоразделом. Расстояние до водораздела от начала координат (х=а) определяется уравнением

(11.69)

Сечение водораздела служит внутренней границей, разделяющей два потока, имеющих противоположные направления фильтрации. Если на междуречье шириной L имеется водораздел подземных вод, то при х=0 q₀<0, а при x=L q_L>0. При изменении уровней воды в реках водораздел смещается в сторону реки, в которой уровень поднимается быстрее. Водораздел на междуречье присутствует, если а больше 0, но меньше L. В остальных случаях водораздел подземных вод на междуречье отсутствует. Если а<0, то любое значение q_х на междуречье больше 0, Если a>L, то любое значение q_x меньше 0.

Если известно положение водораздела а, то

(11.70)

Для построения депрессионной кривой вернемся к уравнению (60)

.

Решая систему этих двух уравнений относительно H_x и h_x, получим

(11.71)

(11.72)

Если q₀ = - a, то

(11.73)

Эти уравнения дают приближенную оценку величин H_x и пригодны лишь при малых уклонах водоупорного ложа i. Если водоупорное ложе горизонтальное, i=0, то H₀=h₀ и

(11.74)

Пример 11.1.

На междуречье шириной 390 м подземные воды со свободной поверхностью обнаружены в мелкозернистых песках с коэффициентом фильтрации 5,8 м/сут. В западной реке уровень воды располагается на отметке 52,4 м, а в восточной реке - 52,59 м. Водоупорное ложе горизонтально и залегает на отметке 46,16 м. Инфильтрационное питание отсутствует.

Определить уровень грунтовых вод в середине водораздела и единичный расход фильтрационного потока.

Решение.

Имеем линейный неограниченный поток безнапорных вод.

h₀ = 52,40 - 46,16 = 6,24 м

h_L = 52,59 – 46,16 = 6,43 м.

м²/сут.

Удельный расход имеет отрицательное значение, так как фильтрация направлена в сторону начала координат.

Высота потока грунтовых вод в середине водораздела вычисляется следующим образом

м.

Тогда отметка уровня грунтовых вод будет H₁₉₅ = 6,336 + 46,16 = 52,496 м.

Пример 11.2.

На склоне заложены две скважины 1 и 2, на расстоянии 1,5 км. В первой из них уровень воды установился выше кровли на абсолютной отметке 250,0 м, во второй - также выше кровли на отметке 248,0 м. Мощность водоносного пласта в этих скважинах равна соответственно 30,0 и 15,0 м. Коэффициент фильтрации пласта 25,0 м/сут.

Определить единичный расход потока и положение установившегося уровня поды в скважине, которую планируется пробурить между скважинами 1 и 2 на расстоянии 500 м от первой.

Решение.

Имеем линейный неограниченный поток напорных подземных вод с изменяющейся мощностью.

Вычислим удельный расход

м²/сут.

Допустим, что мощность потока между скважинами меняется подчиняясь линейной зависимости, тогда мощность водоносного пласта в 500 м от первой скважины будет

м.

Тогда

м.

Пример 11.3.

Водоносная толща, состоящая из трех разных по водопроницаемости песчаных пластов, вскрыта двумя скважинами, расположенными вдоль потока на расстоянии 900 м друг от друга. Нижний пласт имеет мощность 4,1 м и коэффициент фильтрации 12,7 м/сут. Водонасыщенная часть, верхнего пласта имеет мощность 24,2 м в скважине 1 и 6,4 м в скважине 2. Коэффициент фильтрации этого пласта равен 6,3 м1сут. Абсолютные отметки уровня подземных вод 49,0 м в скважине 1 и 38,0 м в скважине 2. Определить удельный расход грунтового потока.

Решение.

Имеем линейный неограниченный поток напорных подземных вод с поперечной неоднородностью. Определим удельный расход

м²/сут.

Пример 11.4.

В скважине 1 вскрыты тонкозернистые пески с коэффициентом фильтрации 0,95 м/сут, насыщенные водой в интервале отметок от 94,0 до 100,4. В скважине 2 вскрыты крупнозернистые пески с коэффициентом фильтрации 22,3 м/сут, водонасыщенные в интервале отметок от 94,1 до 104,6. Необходимо определить единичный расход фильтрации между скважинами и получить данные для построения депрессионной кривой, допустив постепенное изменение свойств песка на расстоянии 580 м между скважинами.

Решение.

Имеем линейный неограниченный поток безнапорных подземных вод с переменным коэффициентом фильтрации. Коэффициент фильтрации находится в линейной зависимости от величины х:

В этом случае

м²сут.

Уровень подземных вод найдем по формуле

Рассчитав последовательно K_x, K_cp.x, H_x для разных значений х в интервале от 0 до 580 м, получим необходимые данные для построения депрессионной кривой:

x, м	1	10	50	100	200	300	400	500	579
Нх, м	100,5	100,9	102,0	102,7	103,4	103,8	104,1	104,3	104,5

Пример 11.5.

Определить единичный расход вод, фильтрующихся из водохранилища в соседний овраг, расположенный на расстоянии 900 м, и определить параметры необходимые для построения депрессионной кривой подземных вод. Известно, что вода из водохранилища фильтруется через супесь речной террасы шириной 50 м, гравелистые пески коренного берега и разгружается в овраг в виде нисходящих источников. Супесь и пески подстилаются горизонтально залегающими глинами. Водонасыщенные супеси у водохранилища имеют мощность 11,6 м и коэффициент фильтрации 1,9 м/сут. Коэффициент фильтрации гравелистых песков равен 20,7 м/сут.

Решение.

Имеем линейный неограниченный поток безнапорных подземных вод с горизонтальным водоупорным ложем. В данном случае неоднородность продольная неупорядоченная потому, что коэффициент фильтрации меняется не постепенно, а резко на границе между участками L₁ и L₂. Так как подземные воды разгружаются в виде источников, можно принять h₂=0. Поэтому

м²/сут.

На участке L₁ (при х меньше 50 м) имеем

.

В пределах коренного берега на границе участков L₁ и L₂:

м.

Тогда для участка L₂ (при х больше 50 м) получим

.

Рассчитанные значения h_x даны в таблице

x, м	10	20	30	50	100	300	500	700	900
hx, м	11,1	10,6	10,1	9,1	8,8	7,5	6,0	4,1	0,0

Пример 11.6.

Междуречье шириной 9 км сложено трещиноватыми известняками, которые подстилаются плотными горизонтально залегающими глинами. Мощность водонасыщенных известняков у рек 83 и 75 м. Коэффициент фильтрации 26 м/сут. В инфильтрационном питании участвует 30% годового количества осадков, которое достигает 380 мм.

Необходимо определить единичный расход подземных вод в реке и данные для построения депрессионной кривой.

Решение.

Имеем линейный неограниченный поток подземных вод. Так как инфильтрационное питание м/сут не равно нулю, величина удельного расхода является функцией расстояния от начала координат х. Единичный расход в левую реку соответствует x = 0. Поэтому

м²/сут.

Единичный расход в правую реку соответствует x = L. Поэтому

м²/сут.

Далее определим значения мощности фильтрационного потока

.

Рассчитанные значения мощности фильтрационного потока даны в табличной форме

x, м	500	1000	2000	3000	4000	5000	6000	7000	8000	9000
hx, м	82,9	82,7	82,3	81,8	81,1	80,2	79,2	78,0	76,6	75,1

Приложения

Таблица 1.

Значения кинематического коэффициента воды , см²/сек ,

в зависимости от температуры.

to		to		to	
1 2 3 4 5 6 7 8 9 10 11	0.017321 0.016740 0.016193 0.015676 0.015188 0.014726 0.014289 0.013873 0.013479 0.013101 0.012740	12 13 14 15 16 17 18 19 20 22 24	0.012396 0.012067 0.011756 0.011463 0.011177 0.010888 0.010617 0.010356 0.010105 0.009892 0.009186	26 28 30 35 40 45 50 55 60	0.008774 0.008394 0.008032 0.007251 0.006587 0.006029 0.005558 0.005147 0.004779

Таблица2.

Значение коэффициента шероховатости n по Н.Н.Павловскому

Катего-рия	Род стенки	n	1/n
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	Исключительно гладкие поверхности; поверхности покрытые эмалью или глазурью Весьма тщательно остроганные доски, хорошо пригнанные. Лучшая штукатурка из чистого цемента Лучшая цементная штукатурка (1/3 песка). Чистые (новые) гончарные, чугунные и железные трубы, хорошо уложенные и соединенные. Хорошо остроганные доски Неостроганные доски, хорошо пригнанные. Водопроводные трубы в нормальных условиях, весьма чистые водосточные трубы, весьма хорошая бетонировка Тесовая кладка в лучших условиях, хорошая кирпичная кладка. Водосточные трубы в нормальных условиях, несколько загрязненные водопроводные трубы Загрязненные трубы (водопроводные и водосточные), бетонировка каналов в средних условиях Средняя кирпичная кладка, облицовка из тесанного камня в средних условиях. Значительно загрязненные водостоки. Брезент по деревянным рейкам Хорошая бутовая кладка, старая (растроенная) кирпичная кладка; сравнительно грубая бетонировка. Исключительно гладкая, весьма хорошо разработанная скала Каналы, покрытые толстым, устойчивым илистым слоем, каналы в плотном лессе и в плотном мелком гравии, затянутые сплошной илистой пленкой Средняя (вполне удовлетворительная) бутовая кладка, булыжная мостовая. Каналы, весьма чисто высеченные в скале. Каналы в лессе, в плотном гравии, плотной земле, затянутые илистой пленкой (в нормальном состоянии) Каналы в плотной глине. Каналы в лессе, гравии, земле, затянутые несплошной (местами прерываемой) илистой пленкой. Большие земляные каналы, находящиеся в условиях содержанияи ремонта выше средних Хорошая сухая кладка. Большие земляные каналы в средних условиях содержания и ремонта и малые в хороших. Реки в весьма благоприятных условиях (чистое прямое ложе со свободным течением, без обвалов и промоин) Земляные каналы, большие в условиях содержания и ремонта ниже средней нормы; малые - в средних условиях Земляные каналы в сравнительно плохих условиях (например, местами с водорослями, булыжником или гравием по дну); заметно заросшие травой; с местными обвалами откосов и пр. Реки в благоприятных условиях течения Каналы, находящиеся в весьма плохих условиях (с неправильным профилем; заметно засоренные камнями и водорослями и пр.). Реки в сравнительно благоприятных условиях, но с некоторым количеством камней и водорослей Каналы в исключительно плохих условиях (значительные промоины и обвалы; заросли камыша; густые корни, крупные камни по руслу и пр.). Реки при дальнейшем ухудшении условий течения (по сравнению с предыдущими пунктами), увеличение количества камней и водорослей, извилистое ложе с небольшим количеством промоин и отмелей и т.д.	0.009 0.010 0.011 0.012 0.013 0.014 0.015 0.017 0.018 0.020 0.0225 0.025 0.0275 0.030 0.035 0.040 и больше	111.1 100 90.9 83.3 76.9 71.4 66.7 58.8 55.6 50.0 44.4 40 36.4 33.3 28.6 25 и меньше

ЛИТЕРАТУРА

1. Альтшуль А.Д., Калицун В.И. Примеры расчетов по гидравлике: Учебное пособие для вузов. - М.: Стройиздат, 1977. - 255 с.

2. Андреевская А.В., Кременецкий Н.Н., Панова М.В. Задачник по гидравлике: Учебное пособие для гидромелиоративных и гидротехнических факультетов и вузов. – М.: Энергия, 1970. – 564 с.

3. Кедров В.С., Калицун В.И. Гидравлика, водоснабжение и канализация: Учебник для вузов. - М.: Стройиздат, 2000. - 397 с.

4. Киселев П.Г. Гидравлика. Основы механики жидкости. – М.: Энергия, 1980. – 360 с.

5. Константинов Н.М., Петров Н.А., Высоцкий Л.И. Гидравлика. Гидрология. Гидрометрия: Учебник для вузов: В 2 ч.- М.: Высшая школа, 1987.

6. Теплов А.В. Основы гидравлики. - Л.: Энергия, 1971. - 208 с.

7. Тихомиров В.В., Болотникова И.В. Практикум по инженерной гидрогеологии. - Л.: ЛГМИ, 1990. - 254 с.

8. Штеренлихт Д.В. Гидравлика: Учеб. для вузов. - М.:Колосс, 2005.- 656 с.