10. Движение жидкости в открытых руслах

Равномерное движение в открытых руслах характеризуется постоянством по длине потока расхода Q, уклона дна i, глубины наполнения h, размеров сечения  и его формы, коэффициента шероховатости стенок n.

Основной формулой для расчета равномерного движения является формула Шези (8.1), где величина коэффициента Шези С определяется по формуле Павловского (7.20) или по формуле Агроскина (7.22).

К основным задачам гидравлического расчета при равномерном движении жидкости относятся:

1. определение Q или i, если заданы все элементы живого сечения, n;

2. определение одного или двух неизвестных элементов живого сечения, если заданы Q, i, n.

Первая задача легко решается по формуле Шези. Вторая задача допускает большое число решений, т.е. является неопределенной. Поэтому необходимы дополнительные данные: либо глубина, либо ширина по дну, либо отношение ширины по дну к глубине. Такая задача решается подбором по формуле Шези.

Гидравлически наивыгоднейшим сечением называется такой профиль, при котором для заданных значений площади живого сечения, шероховатости и уклона дна будет наибольший расход. Гидравлически наивыгоднейшим сечением обладает профиль, у которого смоченный периметр  наименьший. Таковым профилем является полукруг. Однако в практике каналам придают трапецеидальное сечение (рис.10.1), потому что полукруг будет иметь неустойчивые откосы.

Рис.10.1. Трапецеидальное сечение канала

Определим гидравлически наивыгоднейшее соотношение между шириной трапецеидального канала по дну и глубиной воды в нем b/h. Тогда площадь живого сечения

, (10.1)

где m - коэффициент откоса.

Смоченный периметр

. (10.2)

Выразив значение b из выражения (10.1) и подставив его в (10.2) получим

. (10.3)

Так как при гидравлически наивыгоднейшем сечении смоченный периметр должен быть наименьшим, то

, (10.4)

отсюда получим, что

. (10.5)

Глубиной h безнапорного потока называется вертикальное расстояние в его живом сечении от свободной поверхности до самой низкой точки дна русла.

При этом различают глубину нормальную (h₀) и критическую (h_кр). Нормальной называется глубина при равномерном движении жидкости в русле. Критическая глубина - эта та, при которой заданный расход проходит с минимальным значением удельной энергии.

Безнапорные потоки могут иметь три состояния в зависимости от соотношения h к h_кр: бурное (h<h_кр), спокойное (h>h_кр) и критическое (h=h_кр).

Резкий переход потока из бурного состояния в спокойное, т.е. переход от глубины h₁<h_кр к глубине h₂>h_кр, называется гидравлическим прыжком (рис.10.2). Этот переход осуществляется на сравнительно небольшой длине вдоль потока l_п, который называется длиной прыжка.

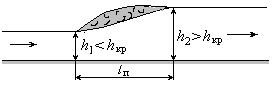
Рис.10.2. Совершенный гидравлический прыжок

Глубины h₂ и h₁ называются сопряженными, а их разность - высотой прыжка.

В зависимости от условий, в которых происходит гидравлический прыжок, наблюдаются различные его виды.

Совершенный гидравлический прыжок (рис.10.2) характеризуется тем, что в зоне прыжка образуется валец, в котором жидкость находится во вращательном движении, у свободной поверхности скорость направлена в обратную сторону. Как показывают опыты, при совершенном прыжке h₂ / h₁ > 2.

В

Рис.10.3. Волнистый гидравлический прыжок

олнистый гидравлический прыжок или несовершенный (рис.10.3) образуется тогда, когда сопряженные глубины близки к критической глубине. Валец при этом не образуется, и прыжок принимает форму ряда постепенно затухающих волн.

Подпертый гидравлический прыжок (рис.10.4), так же как и совершенный имеет хорошо развитый валец, но в отличие от последнего подпирается с низовой стороны стенкой или выступом дна. Поэтому его длина меньше, чем совершенного. Перед стенкой или выступом образуется придонная водоворотная область.

Рис.10.4. Подпертый гидравлический прыжок

Затопленный гидравлический прыжок (рис.10.5) возникает, если глубина потока h больше глубины h₂, являющейся сопряженной с глубиной сооружения h_c в сжатом сечении.

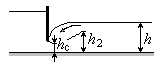
Рис.10.5. Затопленный гидравлический прыжок

В зависимости от расположения по отношению к какому-нибудь характерному сечению (например, расположенному за гидротехническим сооружением или в месте изменения уклона дна канала), выделяются следующие виды гидравлических прыжков: в предельном положении (рис.10.6, а), отогнанный (рис.10.6, б) и надвинутый (рис.10.6, в).

Гидравлические прыжки также подразделяются на прямые, их фронт в плане перпендикулярен направлению движения, и косые, их фронт расположен под углом, не равным 90.

Рис.10.6.

Гидротехнические сооружения (плотины, мосты, водосливы и др.) делят поток на два участка, которые называются бьефами. Участок, лежащий выше гидротехнического сооружения, называется верхним бьефом, а лежащий ниже - нижним бьефом (рис.10.7).

В

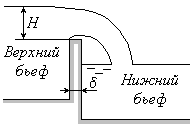Рис.10.7. Водослив

одосливом называется сооружение (стенка), через которую происходит перелив жидкости. Верхняя часть стенки носит название порога. Высота расположения уровня верхнего бьефа над порогом называется напором на водосливе и обозначается Н (рис.10.7).

По форме выреза в стенке водосливы бывают прямоугольные, треугольные, трапецеидальные, круговые (рис.10.8).

Рис.10.8.

По типу стенки водосливы делятся на три вида:

• с тонкой стенкой, у которых толщина стенки  не оказывает влияния на форму переливающейся струи, что выполняется при условии <0,67H;

• с широким порогом, >2H;

• практического профиля, все остальные.

По характеру сжатия струи различают водосливы:

• без бокового сжатия, когда ширина подводящего канала равна ширине отверстия водослива;

• с боковым сжатием, когда ширина подводящего канала больше ширины отверстия водослива.

По характеру сопряжения бьефов водосливы делятся на:

• незатопленные, у которых уровень воды нижнего бьефа не оказывает влияния на горизонт воды верхнего бьефа;

• затопленные, у которых уровень нижнего бьефа влияет на горизонт верхнего бьефа.

Для определения расхода через незатопленный водослив шириной b используется уравнение

. (10.6)

Данное уравнение называется основной формулой расхода через водослив.

Пример 10.1.

Определить среднюю скорость и расход Q в трапециидальном земляном канале при следующих данных: ширина канала по дну b = 8 м; h=2,5 м; m= 1,25; i = 0,0002. Грунт плотный глинистый. Канал в средних условиях содержания и ремонта.

Решение.

1. В соответствие с заданными условиями принимаем по таблице n=0,0225.

2. Вычисляем площадь поперечного сечения , смоченный периметр , гидравлический радиус R, коэффициент Шези C.

 = bh+mh²=82,5+1,252,5²=27,81 м².

 = м.

м^0,5/с, где

3. Подставляем в формулу 8.1 полученные значения и находим

м³/с.

4. Средняя скорость м/с.

Пример 10.2.

Какой уклон i нужно придать каналу из предыдущей задачи, если тот же расход нужно пропустить при h=1,5 м.

Решение.

Так как , то .

 = bh+mh²=81,5+1,251,5²=14,81 м².

 = м.

м^0,5/с, где

.

Пример 10.3.

Определить расход и среднюю скорость в земляном канале параболического сечения при h=2,5 м, параметр параболы р=4 м; i = 0,0002. Канал в средних условиях содержания и ремонта.

Решение.

1. В соответствии с заданными условиями определяем n = 0,025.

2. При  = h / p = 2,9 / 4 = 0,725 вычисляем

м².

 = pN = 42,9 = 11,6 м, где

=2,9 или можно воспользоваться таблицей (см.Андриевская, стр.207)

R = / = 1,61 м.

м

3. Расход

м³/с

4. Средняя скорость потока м/с.

Пример 10.4.

Определить ширину трапецеидального канала по дну при следующих данных: Q = 10,5; h=2,2 м; m = 1,25; n = 0,025;  = 0,0004.

Решение.

1. Задаваясь значением b, находим подбором величину Q. Все расчеты сводим в таблицу.

b			R	C	C	Q
1	8,25	8,04	1,03	44,67	45,33	7,48
1,5	9,08	8,54	1,06	44,91	46,23	8,40
2	10,45	9,04	1,16	45,56	49,07	10,26
2,5	11,55	9,54	1,21	45,91	50,50	11,67

2. По данным таблицы построим график Q = f (b), с помощью которого определим значение b = 2,2.

Пример 10.5.

Определить глубину наполнения трапецеидального канала, пропускной расход Q = 5 м³/с; m = 1; n = 0,025; i = 0,0002, b = 3 м.

Решение.

1. Прежде всего, решим задачу подбором по уравнению, задаваясь рядом значений h. Все расчеты удобно свести в таблицу

h			R	C	C	Q
1	4	5,83	0,69	37,14	30,85	1,74
1,5	6,75	7,23	0,93	39,47	38,06	3,63
2	10	8,64	1,16	41,14	44,31	6,27

2. По данным таблицы построим график Q = f (h), c помощью которого определим h = 1,8.

Пример 10.6.

Определить глубину наполнения параболического канала при пропуске расхода Q = 15,5 м³/с, если р = 2,5; n = 0,0225; i = 0,0006.

Решение.

1. Прежде всего, решим задачу подбором по уравнению Шези, задаваясь рядом значений R. Все расчеты удобно свести в таблицу.

h				R	C	C	Q
1	0,4	2,38	5,05	0,59	40,38	31,02	2,26
2	0,8	8,43	7,75	1,09	45,08	47,06	9,72
2,5	1	11,79	9,03	1,31	46,52	53,24	15,37
3	1,2	15,49	9,03	1,31	46,52	53,24	25,37

2. По данным таблицы строится график Q = f (р), с помощью которого при Q = 15,5 м³/с определим р = 2,6 м.

11. Основы движения подземных вод

Подземной водой называется вода в горных породах, которая может быть в виде пара, капиллярной и гравитационной воды. Капиллярная вода находится в зоне действия капиллярных сил. Под действием силы тяжести и градиента гидростатического давления могут двигаться только гравитационные воды. Фильтрация является основным видом движения подземных вод. Движение подземных вод, так же как в потоках открытых и напорных, может быть установившимся и неустановившимся, равномерным и неравномерным, плавно изменяющимся и резко изменяющимся, напорным и безнапорным, одномерным, двухмерным и трехмерным.

Вода в горных породах движется по порам, трещинам и пустотам, их характеристики определяют фильтрационные свойства грунтов. Наиболее важным является пористость – отношение объема по к объему грунта (достаточно большому по сравнению с размерами частиц грунта и порами)

n = V_п /V. (11.1)

Другой часто используемой характеристикой является коэффициент пористости – отношение объема пор к объему минеральной части (скелета) в данном объеме

е = V_п /V_ск. (11.2)

Часть пор может быть замкнута, вода, содержащаяся в них, не участвует в фильтрационном процессе. Поэтому выделяют общую (абсолютную) пористость и активную (эффективную). В последнем случае учитываются только те поры, через которые движется жидкость.

Так как грунты в целом характеризуются неупорядоченным, случайным расположением частиц и случайным характером порового пространства, то применением теоретического или экспериментального подхода к описанию движения жидкости для конкретных поровых «каналов» или их совокупностей невозможно. Поэтому принимают осредненные по площади скорости.

При изучении фильтрации считаем, что пористое тело и жидкость образуют сплошную среду.

Введем понятие скорости фильтрации

u = Q/ , (11.3)

где Q – расход, проходящий через сечение грунта площадью . Площадь включает как площадь занятую минеральной составляющей, так и поры. Скорость фильтрации считается непрерывной функцией координат и времени. Движение происходит при наличии очень больших сопротивлений в виде малых размеров поровых каналов, их извилистости, неправильной формы, наличию большой шероховатости и ряда других факторов. Это значительно снижает скорость фильтрации. В связи с этим в подземном потоке принимают, что гидродинамический напор Н равен пьезометрическому напору z + p/g, т.е. пренебрегают скоростным напором. В результате изучения движения воды в песчаных фильтрах Дарси установил в 1856 г., что

u = KJ, (11.4)

где K – коэффициент фильтрации (м/сут.), J – градиент напора или гидравлический уклон (J = - dH/dl). Коэффициент фильтрации равен скорости фильтрации при J = 1. Он зависит от свойств пористой среды: формы, размеров, взаимного расположения частиц и шероховатости.

Для решения задач подземной гидравлики первым шагом является типизация сложных гидрогеологических условий. Ниже мы рассмотрим в основном задачи связанные с зоной насыщения, определив ее как зону, в пределах которой повсеместно поровая жидкость образует непрерывную фазу, соответственно здесь имеет место непрерывная передача гидростатического давления во всех точках зоны. Верхней границей зоны насыщения служит свободная поверхность уровней верхнего (грунтового) водоносного горизонта, на которой гидростатическое давление (отсчитываемое от атмосферного давления) равно нулю. В данном случае критерием типизации служит характер водонасыщения и гидростатическое давление. В пределах зоны насыщения также выделяются водоносные горизонты, залегающие между пластами водоупорных (непроницаемых) горных пород.

Р ассмотрим безнапорный фильтрационный поток с постоянным расходом в однородных коллекторах. Его можно представить в виде неограниченного линейного потока безнапорных вод в однородном коллекторе, у которого все границы ориентированные вдоль линий токов, непроницаемые (рис.11.1). Расход воды в таком потоке не меняется; сколько воды втекает в него, столько вытекает из него. Длина потока равна L. В начале потока уровень поды залегает на отметке Н₀, а водоупорное ложе на отметке z₀. В конце потока уровень подземной воды вскрыт на отметке Н_L, а водоупорное ложе z_L. Тогда мощности потока в начале и в конце будут равны . Средний коэффициент фильтрации равен К.

Так как поток неограниченный, определим единичный расход q:

q=Kh_срJ_ср (11.5)

где h_ср и J_ср, вследствие постоянных величин q и K связаны между собой обратной зависимостью. Поэтому для оценки единичного расхода необходимо использовать h_ср и J_ср одного интервала. Если принять, что

тогда

(11.6)

Если водоупорное ложе горизонтально (z₀=z_i; i=0), то гидростатический напор можно рассчитывать не относительно уровня моря, а относительно водоупорного ложа.

В этом случае имеем:

Поэтому

. (11.7)

Для построения депрессионной кривой воспользуемся уравнением (2), которое из-за постоянства q справедливо для любых двух сечений одного потока. Заменим в нем h_L и H_L на h_x и H_x, а L на x. Тогда получим:

. (11.8)

Для участка потока длиной x уклон водоупорного ложа можно выразить через уравнение

. (11.9)

Если известны величины единичного расхода q, коэффициента фильтрации K и уклон водоупорного ложа i, то при заданном значении x уравнения (4) и (5) представляют собой систему с двумя неизвестными h_x и H_x. Решая эту систему уравнений относительно этих неизвестных, получим:

, (11.10)

. (11.11)

Пользуясь уравнением (2), единичный расход можно выразить через граничные условия. Тогда будем иметь

. (11.12)

Если водоупорное ложе горизонтально, то z_x=z₀ и i=0. Тогда можно принять H₀=h₀, H_L=h_L и H_x=h_x. В этом случае уравнения (7) и (8) примут вид

. (11.13)

Уравнения (6), (7), (8) и (9) позволяют определять значения h_x или H_x как функции расстояния от начала координат x. При этом

. (11.14)

Поэтому при построении депрессионных кривых уровня грунтовых вод удобно пользоваться вычислительной техникой.

Однако полученные уравнения являются приближенными и справедливы только при постоянных значениях q, K и i, где уклон водоупорного ложа i имеет не очень большие значения и определяется по уравнению

(11.15)

Если на исследуемом участке длиной L уклон водоупорного ложа заметно меняется, то эти уравнения использовать нельзя. В этом случае необходимо предварительно выделить участки с относительно постоянными уклонами. Между этими участками через точки изменения угла наклона проводятся вертикальные внутренние границы четвертого рода. Полученные выше уравнения пригодны только в границах этих участков. Поэтому, прежде чем их использовать, необходимо определить условия на разделяющих их внутренних границах. К таким условиям относятся величины единичного расхода, гидростатических напоров, мощности фильтрационного потока.

Предположим, что в результате проведенных гидрогеологических исследований установлены: общая длина фильтрационного потока L, гидростатические напоры в реках, разделенных междуречьем Н₀ и H_L, мощности потока в начале (при х=0) 1г₀ и в конце (при x=L) h_L протяженности выделенных участков L₁, L₂, ..., L_i, ..., L_L и гипсометрические отметки водоупорного ложа в точках изменения его угла наклона z₀, z₁, ..., z_j, ..., z_L. Необходимо определить величину единичного расхода q, гидростатические напоры (Н₁, Н₂, ..., Н_j, ..., Н_L-1) и мощности фильтрационного потока (h₁, h₂, ..., h_j, ..., h_L-1,) в сечениях внутренних границ.

Пользуясь уравнением (7), можно определить величину гидростатического напора в сечении j по величине аналогичного напора в предшествующем сечении j-1:

(11.16)

Если бы была известна величина единичного расхода q, можно было бы последовательно определить Н₁ по Н₀, H₂ по Н₁, …, H_j по Н_j-1, и, наконец, H_L по H_L-1.

Поставленная задача решается подбором такой величины q, при которой рассчитанное таким образом значение H_L равно исходному. Задача легко решается с помощью ЭВМ

Напорный фильтрационный поток с постоянным расходом в однородных коллекторах представлен на рис.11.2. Так как притоки воды через водоупорное ложе и кровлю отсутствуют, расход воды в таком потоке не меняется (сколько воды в него втекает, столько же вытекает).

Предположим, что поток имеет длину L, а мощность его меняется от т₀ до m_L постепенно, как линейная функция координаты х:

(11.17)

Рис.11.2. Расчетная схема напорного линейного потока подземных вод с постоянным расходом в однородном коллекторе

Гидростатический напор меняется от H₀ до H_L (рис.11.2).

Согласно уравнению q=Q/B=KhJ в каждом сечении потока единичный расход может быть выражен функцией

(11.18)

В итоге имеем дифференциальное уравнение.

. (11.19)

Интегрируя это уравнение в интервалах значений гидростатического напора H от H₀ до H_L и расстояния х от 0 до L, получим

(11.20)

Из этого уравнения видно, что среднему значению градиента напора (H₀ — H_L)/L при линейном изменении мощности водоносного пласта соответствует средняя мощность, определяемая по уравнению

. (11.21)

При относительно малом и неупорядоченном изменении мощ­ности фильтрационного пласта ее средняя величина принимается постоянной т.

Для определения депрессионной кривой воспользуемся уравнением (16), подставив в него вместо параметров сечения L параметры любого сечения на расстоянии х от начала координат. При постоянстве расхода справедливо уравнение

. (11.22)

Решая это уравнение относительно Н_х, получим

. (11.23)

При этом т_х рассчитывается по уравнению (13).

В случае постоянной мощности водоносного пласта т уравнение (19) приобретает вид

(11.24)

Уравнения (19) и (20) легко программируются. Но они справедливы только для участков с относительно постоянной или линейно меняющейся мощностью водоносного пласта.

Если на исследуемой части фильтрационного потока заметно меняется градиент изменения мощности водоносного пласта, то необходимо выделять участки, в которых его мощность либо не меняется, либо меняется, подчиняясь только одной линейной функции. Между участками проводятся внутренние вертикальные границы четвертого рода. Уравнения (18), (19) и (20) пригодны только в границах отдельных участков. Поэтому для их использования необходимо определить граничные условия этих участков: единичный расход и гидростатические напоры.

Предположим, установлены общая длина фильтрационного потока L и гидростатические напоры в его начале и конце (H₀, H_L). Однако известно, что мощность водоносного пласта вдоль потока то уменьшается, то увеличивается. Мощности пласта установлены в начале, конце и в нескольких сечениях потока и имеют значения т₀, т₁, ..., т_j, ... ,т_L.

Согласно уравнению (19) гидростатический напор в любом сечении может быть рассчитан по гидростатическому напору в предыдущем сечении:

. (11.25)

Поэтому, если бы была известна величина постоянного единичного расхода q, то можно было бы последовательно рассчитать значения Н₁, Н₂, ..., Н_j, ..., Н_L. Однако величина Н_L известна. Поэтому задача решается подбором такой величины q, при которой рассчитанное значение Н_L равно заданной величине. Задача легко решается на ЭВМ с использованием циклов. Число циклов должно быть равно числу выделенных участков с постоянными градиентами изменения мощности водоносного пласта.

Напорно-безнапорным называется поток подземных вод, верхней границей которого на разных участках служат свободная водная поверхность и водоупорная кровля. Такие потоки формируются при выходе на поверхность земли водоносных пластов с напорными водами.

Предположим, что переток подземных вод через междуречье осуществляется через песчаный пласт, сверху и снизу ограниченный водоупорными глинами (рис.11.3). Уровень воды одной реки расположен выше кровли этого водоносного пласта, а уровень другой реки - ниже. Водоносный пласт залегает горизонтально и однороден по своим фильтрационным свойствам.

Рис.11.3. Расчетная схема напорно-безнапорного линейного потока подземных вод с постоянным расходом в однородном коллекторе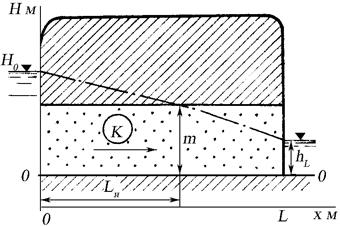

Длина потока L. Мощность пласта водоносных песков постоянна и равна т. Средняя величина коэффициента фильтрации этого пласта равна К. При горизонтальном залегании водоупорного ложа гидростатический напор можно рассчитывать от плоскости основания водоносного пласта. Со стороны реки, в которой уровень воды выше кровли пласта, имеем напорные подземные воды. Граничный гидростатический напор на урезе этой реки можно принять равным превышению уровня воды в реке над уровнем водоупорного ложа H₀. Со стороны реки, в которой уровень воды ниже кровли водоносного пласта, имеем безнапорные подземные воды с граничным гидростатическим напором, равным мощности водонасыщенных песков на урезе этой реки h_L. Таким образом, весь поток подземных вод делится на два участка: напорный и безнапорный. Примем неизвестную величину длины напорного участка равной L_H.

Если бы была известна величина L_H, то значения q в напорном и безнапорном участках потока можно было бы рассчитать, пользуясь уравнениями

, (11.26)

. (11.27)

Так как величина расхода постоянна, мы имеем систему из двух уравнений с двумя неизвестными q и L_H. Решая эту систему урав­нений относительно этих неизвестных, получим

, (11.28)

. (11.29)

Депрессионная кривая строится раздельно для напорного и безнапорного участков. В напорной части потока депрессионная кривая рассчитывается по уравнению (20)

, (11.30)

где х — расстояние от начала напорного участка потока.

В безнапорной части потока депрессионная кривая рассчитывается по уравнению (9)

, (11.31)

где х - расстояние от начала безнапорного участка потока.

Фильтрационные потоки с постоянным расходом в неоднородных коллекторах выделяются в случае, если коэффициент фильтрации в границах отдельного водоносного пласта заметно меняется. Если его максимальные и минимальные значения отличаются менее чем в 10 раз, коллектор можно считать относительно однородным. В этом случае величина коэффициента фильтрации, используемая для характеристики модельного потока, определяется, как среднеарифметическая всех его определений:

(11.32)

где К_j - значения замеренных величин коэффициента фильтрации; п - число этих значений.

Когда максимальное и минимальное значения замеренных величин коэффициента фильтрации в пределах одного водоносного пласта различаются более чем в 10 раз, коллектор следует считать неоднородным. В этом случае расчет средней величины коэффициента фильтрации в используемом модельном потоке зависит от типа неоднородности.

Различают поперечную (или слоистую) и продольную неоднородности. Под поперечной (слоистой) неоднородностью понимают неоднородность, при которой наибольшие изменения коэффициента фильтрации наблюдаются в направлениях, перпендикулярных линиям токов. В этом случае каждая отдельная струйка потока фильтруется в однородной среде, но среды разных струек разные.

При продольной неоднородности наибольшие изменения коэффициента фильтрации наблюдаются вдоль линий токов. В этом случае каждая струйка потока фильтруется в неоднородной среде.

Предположим, что необходимо, определить количество воды, которое фильтруется из одной реки в другую через междуречье, и построить депрессионную кривую, если водоносный пласт состоит из нескольких слоев с разными коэффициентами фильтрации и сверху перекрыт водоупорной кровлей, т.е. имеем фильтрационный поток с постоянным расходом в коллекторе с поперечной (слоистой) неоднородностью. Если уровни воды в реках расположены выше водоупорной кровли, то фильтрационный поток имеет напорный характер.

Предположим, что в состав водоносного пласта входит п слоев с коэффициентами фильтрации K₁, K₂, …, K_j,…, K_n и мощностями т ₁, т ₂, …, т _j,…, т _n (рис.11.4). Когда линии токов фильтрационного потока ориентированы вдоль слоев, единичный расход потока можно представить как сумму единичных расходов отдельных слоев

. (11.33)

Умножив и разделив правую часть этого уравнения на суммарную мощность пласта т, получим

Рис.11.4. Расчетная схема линейных потоков подземных вод при поперечной (слоистой) неоднородности коллектора

(11.34)

Из этого уравнения следует, что в случае поперечной (слоистой) неоднородности средний коэффициент фильтрации рассчитывается по уравнению

. (11.35)

Это уравнение применимо лишь к фильтрационным потокам, в которых линии токов ориентированы вдоль отдельных слоев и не пересекают границы между ними. Поэтому оно может использоваться только в случае напорных фильтрационных потоков.

В случае безнапорных вод линии токов криволинейны и при поперечной неоднородности пересекают границы между слоями разной проницаемости. Поэтому использовать общий средний коэффициент фильтрации в случае поперечной неоднородности безнапорных вод не рекомендуется.

При незначительных градиентах напора, когда уровень грунтовых вод не выходит за границы одного однородного по проницаемости слоя, можно допустить, что линии токов в остальных слоях ориентированы вдоль разделяющих их границ. Тогда общий расход водоносного пласта с поперечной (слоистой) неоднородностью можно представить как сумму двух слагаемых: расхода безнапорного потока в самом верхнем не полностью насыщенном слое и расхода остальных полностью насыщенных слоев.

Предположим, что междуречье сложено слоями пород разной проницаемости. Мощности слоев: т ₁, т ₂, …, т _j,…, т_n, соответствующие коэффициенты фильтрации: K₁, K₂, …, K_j,…, K_n. При этом уровни воды в реках, разделенных междуречьем, располагаются так, что самый верхний слой насыщен не полностью. Водонасыщенная часть его при x=0 равна h_n0, а при x = L равна h_nL. В этом случае общий расход водоносного пласта можно представить как сумму

. (11.36)

Тогда

(11.37)

Депрессионная кривая в этом случае строится относительно нижней границы верхнего водоносного слоя и согласно уравнению (11). В этом случае

. (11.38)

Если уровень безнапорных вод сечет границы между отдельными слоями водоносного пласта, то коэффициент фильтрации меняется и вдоль линии тока. Эта продольная неоднородность имеет наибольшее значение для верхней части водоносного пласта, и ее необходимо учитывать. Для этих целей используется функция Н.К.Гиринского, которая может быть выражена уравнением

, (11.39)

где h - общая мощность фильтрационного потока; z_j - расстояние по вертикали от водоупорного ложа до середины каждого отдельного слоя j.

. (11.40)

Эта функция рассчитывается для конкретного сечения и имеет размерность общего расхода.

Для определения единичного расхода безнапорного фильтрационного потока с поперечной (слоистой) неоднородностью по функции Гиринского прежде всего рассчитываются значения g для сечений при x = 0 и x=L. Единичный расход определяется согласно уравнению

. (11.41)

Величина функции Гиринского находится в прямой линейной зависимости от значения х. Поэтому

. (11.42)

Зная величину g_x, можно рассчитать величину h_x.

Фильтрационный поток с постоянным расходом в коллекторах с продольной неоднородностью. При продольной неоднородности величина коэффициента фильтрации может меняться плавно и закономерно или резко и непоследовательно. Продольная неод­нородность, при которой величина коэффициента фильтрации меняется постепенно, как функция пути фильтрации, называется упорядоченной. Продольная неоднородность при которой наблюдается чередование участков с разной, но относительно постоянной средней проницаемостью называется неупорядоченной.

Предположим, что на исследуемом нами междуречье коэффициент фильтрации меняется вдоль фильтрационного потока постепенно от значения K₀ при х = 0 до K_L при x=L. Фильтрационный поток сверху ограничен водоупорной кровлей и имеет постоянную мощность m (рис.11.5). Можно допустить присутствие линейной зависимости между К и х:

. (11.43)

Т

Рис.11.5. Расчетная схема линейного потока напорных подземных вод

при продольной упорядоченной неоднородности коллектора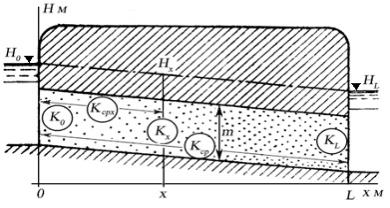

огда единичный расход в любом сечении х можно выразить в виде дифференциального уравнения

или

. (11.44)

Интегрируя левую часть последнего уравнения в интервале значении х от 0 до L, а правую в интервале соответствующих значений гидростатического напора от Н₀ до H_L и решая его относительно единичного дебита получим

(11.45)

Из уравнения (41) следует, что в случае продольной упорядоченной неоднородности средний коэффициент фильтрации можно рассчитывать, пользуясь уравнением

(11.46)

Это уравнение справедливо и для безнапорных вод. Поэтому для последних применимо уравнение

. (11.47)

В тех случаях, когда продольная упорядоченная неоднородность сопровождается изменением мощности водонасыщенного пласта, можно допустить линейную зависимость между водопроводимостью (Т=тК) и расстоянием фильтрации согласно уравнению

В этом случае аналогичным образом можно показать справедливость уравнения

(11.48)

При построении депрессионной кривой в условиях продольной упорядоченной неоднородности необходимо учитывать переменный характер величины среднего коэффициента фильтрации. Согласно уравнению (19) в случае напорных подземных вод

(11.49)

Пли пользуясь уравнением (44), можно записать короче

(11.50)

Если в этом уравнении выразить q через граничные условия при x=0 и x=L согласно уравнению (41), тогда

. (11.51)

В случае безнапорных подземных вод

. (11.52)

Когда фильтрационные свойства коллектора меняются вдоль линий токов резко и неупорядоченно, то имеем случай продольной неупорядоченной неоднородность, тогда вдоль потока выделяются участки, в пределах которых величины коэффициентов можно принять постоянными. Таким образом, весь поток делится внутренними границами четвертого рода на l участков длиной L₁, L₂, …, L_j, …, L_l. Каждый из них имеет свой средний коэффициента фильтрации К₁, К₂, ..., К_j, ..., К_l. (

Рис. 11.6. Расчетная схема линейного потока безнапорных подземных вод при продольной неупорядоченной неоднородности коллектора

рис.11.6).

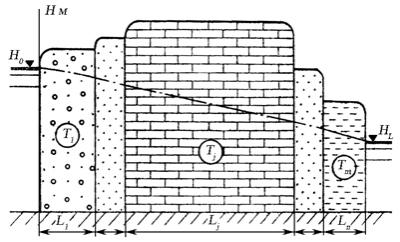
В этом случае единичный расход подземных вод в границах каждого отдельного участка можно определить через уравнение

. (11.53)

Из этого уравнения следует, что

. (11.54)

Так как величина на всех выделенных участках имеет одно и то же значение,

. (11.55)

Следовательно,

. (11.56)

Из этого уравнения следует, что в случае продольной неупорядоченной неоднородности среднему градиенту напора всего потока в целом соответствует

. (11.57)

Если мощность пласта постоянна, то

. (11.58)

Поэтому средний коэффициент фильтрации в случае продоль­ной неупорядоченной неоднородности определяется уравнением

. (11.59)

В тех случаях, когда фильтрация подземных вод направлена перпендикулярно к напластованию, длины участков разной проницаемости равны мощности отдельных пластов (L_j=m_j). Поэтому при оценке перетока подземных вод через водоупорные комплексы

. (11.60)

Для построения депрессионной кривой в случае продольной неупорядоченной неоднородности прежде всего необходимо определить значения гидростатического напора в сечениях внутренних границ.

Если известна величина единичного расхода, то эти значения можно рассчитать, пользуясь рекуррентными уравнениями:

для напорных вод

,

для безнапорных вод

. (11.61)

Определив граничные условия выделенных участков с постоянными коэффициентами фильтрации, рассчитывают депрессионные кривые в границах этих участков, пользуясь уравнениями (20) или (7).