Задача на максимум выпуска.

Пусть лимитирующий объем издержек С равен 150. Цены на ресурсы и равны 5 и 10 соответственно, т.е. . Также предположим, что константа равна 3, а параметр равен .

Найти объем ресурсов и , при которых объем продукции, определяемый производственной функцией максимален. Назовем базисным объемом продукции, т.е. .

Задачу решить двумя способами:

1. Используя теорему К-Т.

2. Пользуясь надстройкой «Поиск решения» MS Excel.

Сравнить значения в точке К-Т и «Множитель Лагранжа» из отчета по устойчивости надстройки «Поиск решения».

Увеличить предельное значение издержек С на единицу. Снова решить задачу, пользуясь надстройкой «Поиск решения» MS Excel. Сравнить полученное значение объема продукции с базисным .

Проиллюстрировать полученное решение диаграммами, построив изокосты соответствующие 3 уровням -С, С-С/3 , С+С/3 и изокванты, соответствующие 3 уровням , , . На этой диаграмме построить градиенты изокосты и изокванты в точке К-Т (можно вручную!).

Определить предельную норму замены одного занятого фондами в оптимальной точке.

Решение.

Для перехода к более привычным обозначениям введем вместо и соответственно. Множество точек удовлетворяющих соотношению называются изокостой уровня С. Другими словами изокоста это линия равной цены, координаты каждой точки на этой линии определяют количество ресурса каждого вида, которые можно приобрести, затратив С денежных единиц.

Областью допустимых значений задачи нелинейной оптимизации в координатах и определяемой соотношениями (*.5) и (*.6) является треугольник, ограниченный осями координат и изокостой С =150 ( ). Область приведена на рис.*.1 и заштрихована.

На рис. также показаны линии уровня функции (*.9). Линии уровня производственной функции называются изоквантами. Координаты каждой точки на этой линии удовлетворяют уравнению . Другими словами изокванта это линия равного объема производства, координаты каждой точки на этой линии определяют количество ресурса каждого вида, затратив которые можно произвести единиц продукции.

Судя по взаимному положению области и линий уровня, задача состоит в том, чтобы найти точку касания самой нижней линии уровня, которая лежит выше заштрихованного треугольника. Другими словами, требуется найти такую изокванту, которая касается заданной изокосты.

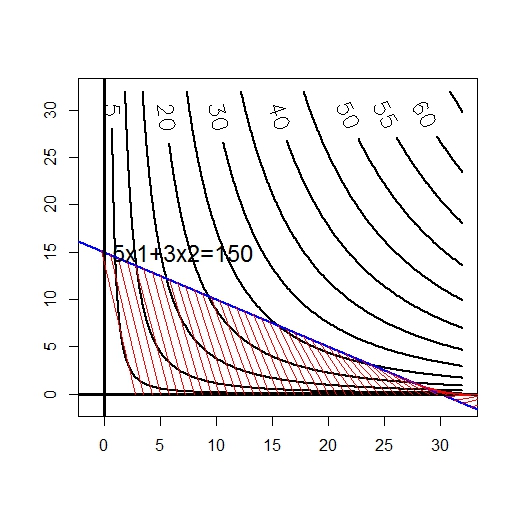
Рис.*.1. Изокванты и область допустимых значений функции нелинейной оптимизации в координатах и определяемая соотношениями (*.5) и (*.6) заштрихована.

Поскольку условия теоремы К-Т сформулированы для нахождения минимума, то введем . С учетом этих обозначений задача на максимум выпуска может быть сформулирован как нелинейная задача на минимум с ограничениями.

(*.10)

(*.11)

(*.12)

Введем функции , и используя соотношения, приведенные ниже.

	(*.13)
	(*.14)
	(*.15)

Преобразуем соотношения (*.12)и (*.11) используя вновь введенные функции. Ограничения (*.12) преобразуется к виду

	(*.16)
	(*.17)

Ограничение (*.11) преобразуется к виду

(*.18)

Целевая функция (*.7) примет вид (*.19)

(*.19)

Область допустимых значений функции нелинейной оптимизации в координатах и определяемая соотношениями (*.16), (*.17) и (*.18) приведена на рис.*.2 и заштрихована. На рис. также показаны линии уровня оптимизируемой функции и направление градиента в некоторых точках.

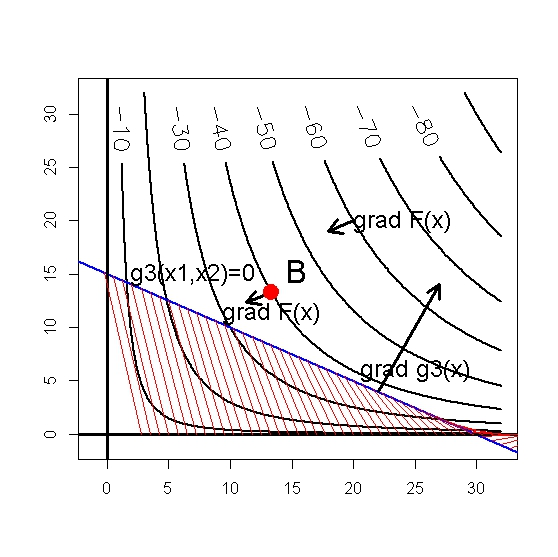
Рис.*2. Область допустимых значений задачи нелинейной оптимизации и линии уровня целевой функции.

Все функции ограничений-неравенств афинны, а значит, выпуклы, поэтому область допустимых значений в задаче выпукла. Заметим, что если взять некоторую точку внутри области, например, , то эта точка будет допустимой и все неравенства в ней выполняются строго . Отсюда следует что область регулярна во всех точках.

Вычислим градиент целевой функции задачи.

(*.20)

Для проверки выпуклости вычислим её Гессиан (матрицу вторых производных).

(*.21)

.

Вычислим главные миноры равны и . Первый минор равен и он положителен при любых значениях аргументов. Второй минор . Оба минора неотрицательны, поэтому по критерию Сильвестра матрица неотрицательно определена. Поскольку для выпуклости дважды дифференцируемой функции необходимо и достаточно неотрицательной определенности Гессиана, то функция выпукла во всей области определения. Таким образом, выполнение условий Куна-Таккера в некоторой точке будут необходимыми и достаточными условиями того, что эта точка является решением задачи.

Вычислим градиенты функций-ограничений.

(*.22)

(*.23)

(*.24)

Чтобы использовать условия Куна-Таккера, необходимо установить набор активных ограничений-неравенств в точке решения.

Взаимное расположение области допустимых значении, линии уровня и направления градиента на рис.*.2 позволяют высказать следующие соображения относительно возможной точки условного минимума. Линии уровня , определяемые уравнением . Возьмем, например, точку В с координатами эта точка не принадлежит области допустимых значений. Через нее проходит линия уровня . Будем мысленно сдвигать линию уровня в направлении градиента (в направлении, показанном стрелкой). Будем сдвигать линию до тех пор, пока она не коснется заштрихованной области. Можно предположить, что касание произойдет в точке принадлежащей прямой (рис.П.3), Поэтому, предположим, что активным является ограничение 3, которое определяют подозрительную точку А на рис.*.3. Тогда для этой точки система будет иметь вид

(*.25)

Используя явное выражение для этих функций, получаем следующее соотношение.

(*.26)

Упростим это соотношение

(*.27)

Запишем это соотношение в виде системы уравнений

(*.28)

Поделим первое уравнение на второе получим

(*.29)

Из этого следует

(*.30)

Поскольку точка А принадлежит прямой , то получаем уравнение.

(*.30)

Это уравнение просто решается, после этого определяем искомые и . После этого вычислим . Из второго уравнения системы(*.28) следует, что .

Поскольку величина положительна и все остальные условия теоремы К-Т выполнены, то в точке А действительно достигается решение оптимизационной задачи. Геометрический смысл соотношения (*.25) показан на рис.*.3. Вектор антиградиент колинеарен и одинаково направлен с вектором поскольку с коэффициент положителен. Таким образом, оптимальное решение задачи ((*.15)-( *.19) достигается при и . Целевая функция (*.10) при этом равна

(*.31)

Таким образом, максимальный объем продукции достигается при и равными 20 и 5 соответственно.

Рис.*.3. Точка А –точка К-Т.

Решение в MS Excel (надстройка «Поиск решения»).

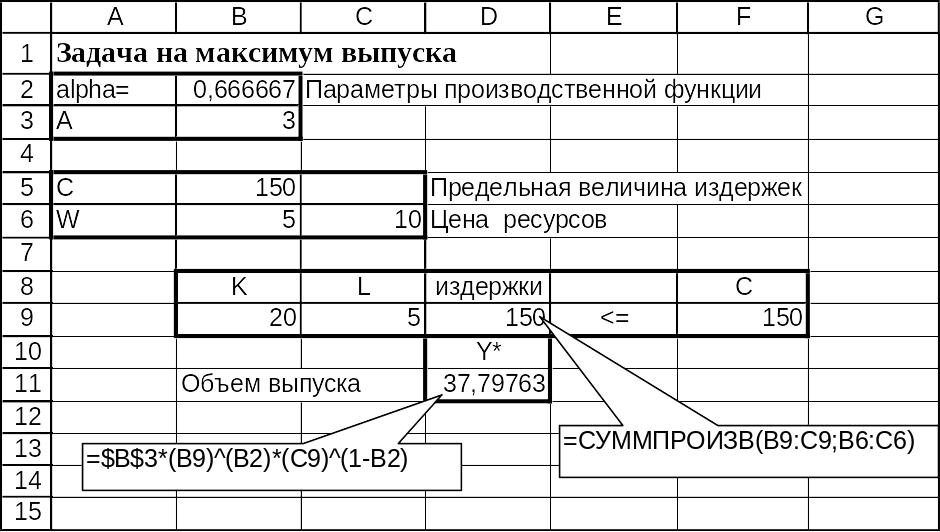
Рис.*.4. Фрагмент электронных таблиц Excel в режиме отображения данных. Нахождение базисного оптимального решения.

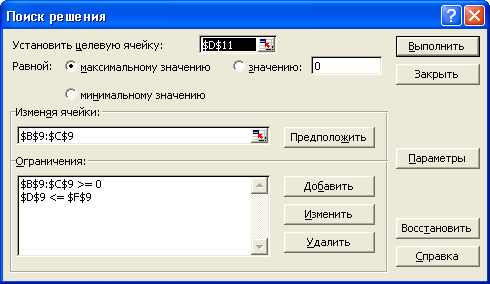
Рис.*.6. Диалоговое окно надстройки «Поиск решения» при поиске оптимального решения.

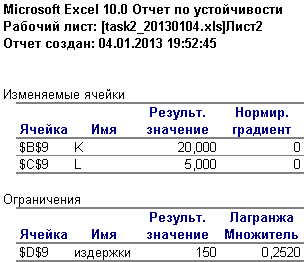
Рис.*.7. Фрагмент электронных таблиц Excel с отчетом по устойчивости

Увеличим предельное значение издержек С на единицу, т.е. примем равным 151. Снова решим задачу, пользуясь надстройкой «Поиск решения» MS Excel (См. рис.*.8).

Новое значение объема продукции Y равно 38,0496, которое находится в ячейке D11. Сравним полученное значение с базисным , вычислив разность . Заметим, что эта разность равна множителю в точке К-Т и «Множитель Лагранжа» из отчета по устойчивости надстройки «Поиск решения» (рис.*.7). Т.е множитель в точке К-Т и «Множитель Лагранжа» из отчета по устойчивости показывает на сколько изменится объем выпуска при увеличении предельной величины издержек на единицу.

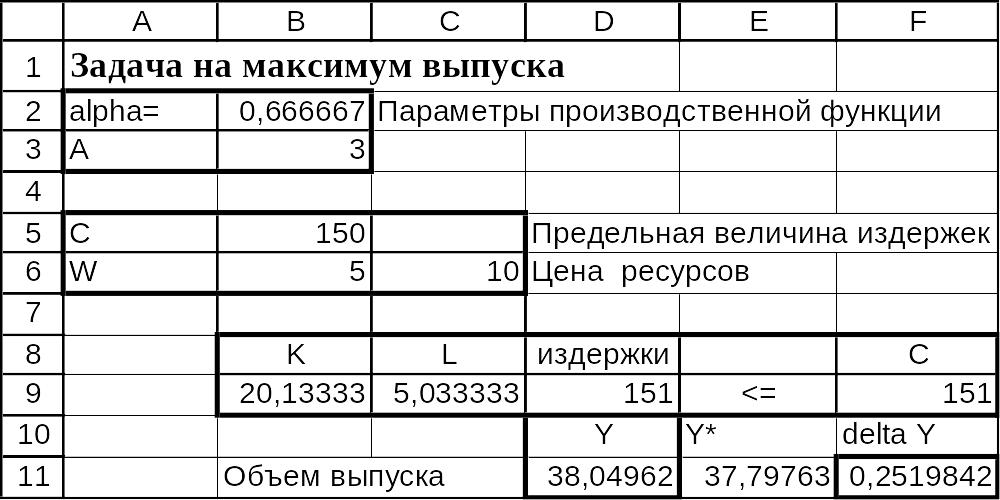
Рис.*.8. Фрагмент электронных таблиц Excel в режиме отображения данных. Сравнение базисного оптимального решения и нового решения при повышении предельного уровня издержек на единицу.

Чтобы проиллюстрировать полученное решение диаграммами с помощью изокост (соответствующие 3 уровням –С=100, С=150, С=200 ) и изоквант, (соответствующие 3 уровням 25 , 37.8, 50), затабулируем соответствующие функции (рис.*.9). Соответствующая диаграмма приведена на рис.*.10. Эта диаграмма является упрощенным вариантом рис.*.3. Точка соответствующая оптимальным значениям выделена. В ней изокванта соответствующая уровню =37.8 и изокоста соответствующая С=150 касаются и следовательно градиенты коллинеарны. Стрелки градиентов при самостоятельном решении можно нанести любым способом, в т.ч. вручную.

Рис.*.9. . Фрагмент электронных таблиц Excel в режиме отображения данных. Табулирование функций для построения изоквант и изокост.

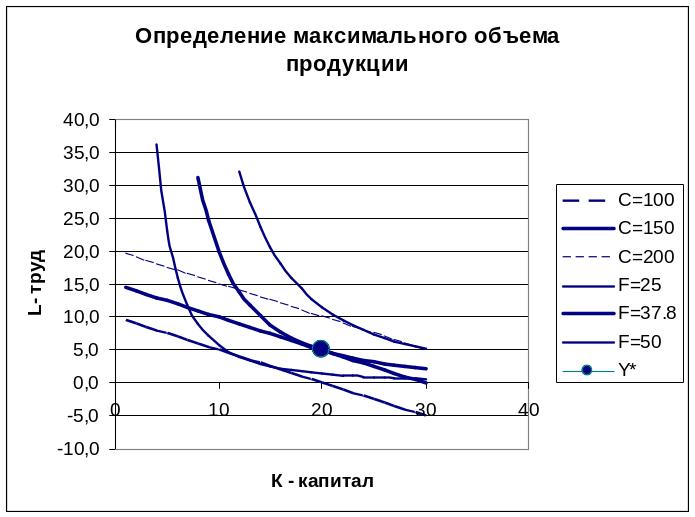
Рис.*.10. . Изокванты и изокосты. Точка соответствующая оптимальным значениям выделена

Определим - предельную норму замены единицы труда (одного занятого) капиталом (фондами) в оптимальной точке.

(*.*)

Это соотношение в первом приближении может быть сформулировано следующим образом: «один работающий может быть заменен двумя единицами фондов».

Используя понятие дифференциала функции многих переменных, приходим к более правильной трактовке полученного соотношения. Эта трактовка выглядит следующим образом: «Если параметры фирмы соответствуют найденной точке К-Т, то увеличение объема продукции может быть достигнуто как увеличением труда, так и увеличением капитала. При этом увеличение объема продукции, достигаемое увеличением труда на единицу будет равно увеличению объема продукции, достигаемое увеличением капитала на две единицы».

Заметим, что этот результат можно получить, используя геометрический смысл Т-К.

Вывод.

• Оптимальное значение количество капитала и труда равно 20 и 5 соответственно, максимальный объем продукции при этом равен 37,7976.

• В точке с координатами и равными 20 и 5 изокоста с уровнем 150 и изокванта с уровнем 37,7976 касаются, а градиенты к ним коллинеарны.

• Решение было получено двумя способами, результаты полностью совпали.

• Значение коэффициента Лагранжа равно 0,2520. Эта величина показывает, насколько увеличивается объем продукции при увеличении объема предельного значения издержек на единицу.

• Предельная норма замены единицы труда (одного занятого) капиталом (фондами) в оптимальной точке равна двум.

Задача 1.