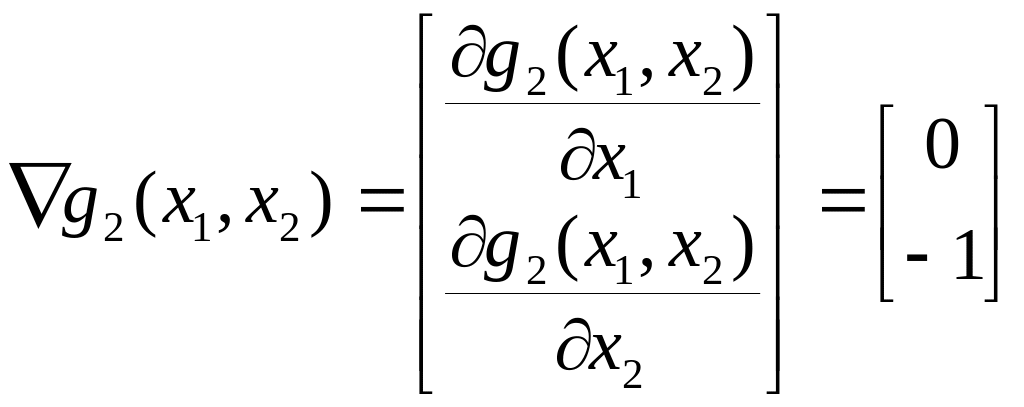Пример 1.
Найти
минимум
функции с ограничениями.
|
(*.1)
|
с ограничениями
|
(*.2)
|
|
(*.3)
|
Для
приведения задачи оптимизации к
стандартному виду введем функции
и
.
|
(*.4) |
|
(*.5) |
Все функции ограничений-неравенств
афинны,
а значит, выпуклы, поэтому область
допустимых значений в задаче выпукла.
Заметим, что если взять некоторую точку
внутри области, например,
,
то эта точка будет допустимой и все
неравенства в ней выполняются строго
.
Отсюда следует что область регулярна
во всех точках.
Вычислим градиент целевой функции задачи.
|
(*.6) |
Для проверки выпуклости вычислим её Гессиан (матрицу вторых производных).
|
(*.7) |
.
Вычислим главные миноры равны
и
.
Первый минор равен
и он положителен при любых значениях
аргументов. Второй минор
.
Оба минора положительны, поэтому по
критерию Сильвестра матрица положительно
определена. Поскольку для выпуклости
дважды дифференцируемой функции
необходимо и достаточно неотрицательной
определенности Гессиана, то функция
выпукла
во всей области определения. Таким
образом, выполнение условий Куна-Таккера
в некоторой точке будут необходимыми
и достаточными условиями того, что эта
точка является решением задачи.
Вычислим градиенты функций-ограничений.
|
(*.8) |
|
(*.9) |
|
|
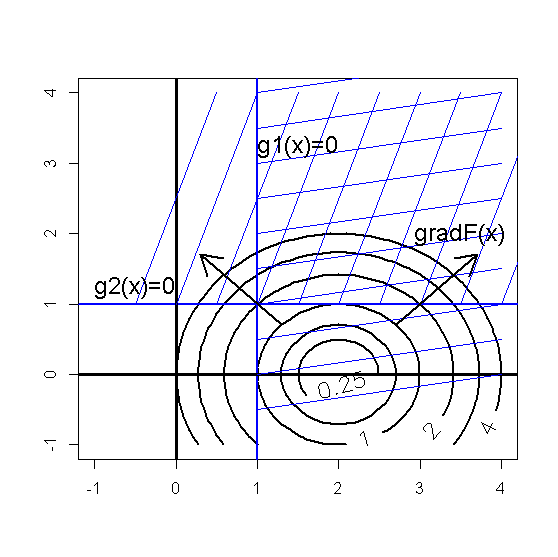
Рис.*.1. Линии уровня и область допустимых значений функции нелинейной оптимизации.
Чтобы использовать условия Куна-Таккера, необходимо установить набор активных ограничений-неравенств в точке решения.
Предположим,
что
т.е. в точке решения нет активных
ограничений неравенств. Условия
экстремума примут вид
.
Это условие дает точку с координатами
и
,
которая является безусловным минимумом
функции
.
В ней нарушаются ограничения с номерами
1 и 2, поэтому данная точка не будет
являться решением в задаче с ограничениями.
Включим
нарушенные ограничения 1 и 2 в число
предполагаемых активных, приняв гипотезу
.
Система условий Куна-Таккера будет
иметь вид
|
(*.25) |
|
(*.25) |
Поскольку
в точке А
и
|
(*.25) |
|
(*.25) |
|
|
|
(*.25) |
Поскольку
отрицательно, то условия К-Т не выполняются.
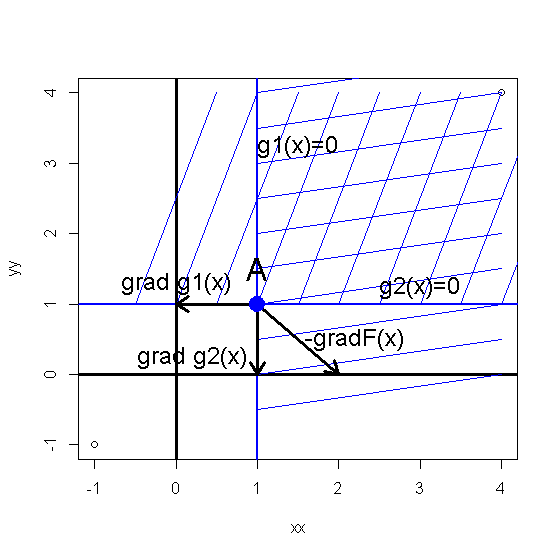
Рис.*.2. Угловая точка области допустимых значений и градиенты ограничений и целевой функции.
Влияние
знака «минус» у множителя (отрицательное
значение)
на поиск условного минимума, иллюстрируется
следующим рис. Красная линия MA
перпендикулярна вектору антиградиента
и она является касательной к линии
уровня в точке А. Эта линия разбивает
пространство на две полуплоскости. В
полуплоскость, лежащую ниже линии MA,
указывает вектор антиградиент. Учитывая,
что направление вектора антиградиента
указывает направление убывания функции,
приходим к выводу, что любое перемещение
( достаточно малое) от точки А в
внутрь нижней полуплоскости, приводит
к уменьшению функции
.
При этом перемещение от точки А
внутрь конуса MAN приводит
к уменьшению значения
,
при этом новая точка, например А’
c координатами
оказывается допустимой.
Это
показывает, что в точке А с координатами
и
условного минимума нет. Т.о. есть смысл
в сдвиге внутрь конуса в направлении
противоположном
,
т.е. ограничение неравенство
перестает быть активным.
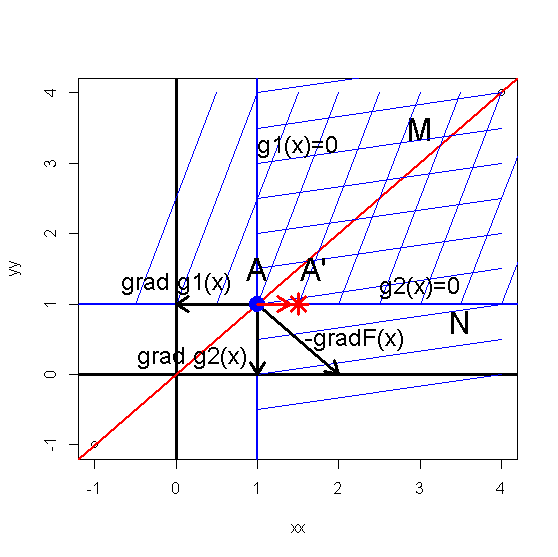
Рис.*.2. Угловая точка области допустимых значений и градиенты ограничений и целевой функции. Переход к новой системе ограничений.
Поэтому
примем гипотезу
.
Система условий Куна-Таккера будет
иметь вид
|
(*.25) |
|
(*.25) |
Поскольку
на прямой
выполняется равенство
.
|
(*.25) |
|
(*.25) |
|
|
Эта система имеет решение
|
|
Поскольку
положительно, то условия К-Т выполняются.
Вектор
антиградиент
колинеарен
и одинаково направлен с вектором
поскольку с коэффициент
положителен. Таким образом, координаты
точки В
и
.
В ней целевая функция достигает условного
минимума, равного 1. Через эту точку
проходит линия уровня 1 (
),
что и показано на рис. *.4
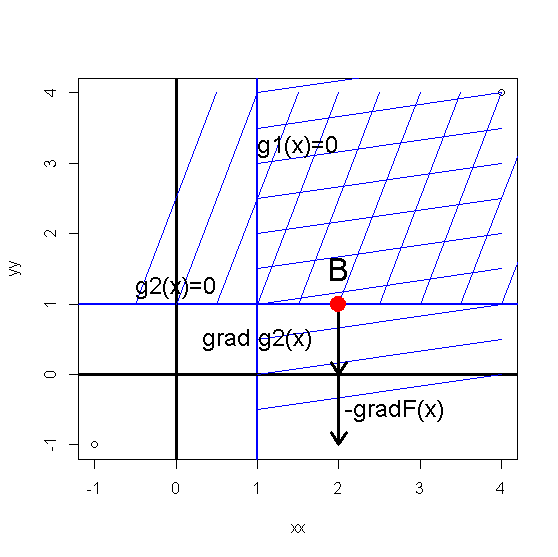
Рис.*.3. Точка В – точка К-Т области.
Рис.*.4. Точка В и линии уровня целевой функции.
6. Модель фирмы
6.1. Экономико-математическая модель задачи
Пусть производственная фирма выпускает один вид продукции.
Обозначим
через Y
- годовой
выпуск фирмы в натурально-вещественной
форме. Для
производства продукции фирма использует
трудовые ресурсы в объеме
(labor,
труд)- среднее
число занятых в год,
и основные
производственные фонды в объеме -
(capital).
Пусть
- вектор-столбец
возможных объемов затрат различных
видов ресурсов.
Тогда объем
продукции фирмы определяется
производственной функцией вида:
|
(*.1)
|
где
-
дважды непрерывно
дифференцируемая функция и матрица ее
вторых производных
отрицательно
определена.
|
(*.2)
|
Рассмотрим функцию прибыли:
|
(*.3)
|
где
–
цена единицы продукции.
- вектор-строка цен ресурсов;
-
цена производственных фондов,
- цена труда.
Произведение
является суммарной величиной затрат и
может быть представлено в развернутом
виде следующим образом.
|
(*.4)
|
Пусть объем издержек, т.е. суммарная величина затрат, ограничен некоторой величиной С. Это условие задается соотношением (*.5)
|
(*.5) |
Важным естественным ограничением является неотрицательность используемых ресурсов и или с учетом ранее введенного обозначения.
|
(*.6)
|
При этих условиях возникают две важные задачи:
1. задача на максимум выпуска
2. задача на максимум прибыли.
Задача на максимум выпуска может быть сформулирована следующим образом. Найти объемы ресурсов и , которые обеспечивают наибольший объем продукции . Т.е. найти максимум при ограничениях (*.5) и (*.6):
|
(*.7) |
Задача
на максимум прибыли может быть
сформулирована следующим образом. Найти
максимум
при ограничениях (*.5) и (*.6):
|
(*.8)
|
где - цена единицы готовой продукции.
В
качестве производственной функции
может
быть рассмотрена функция Коба-Дугласа.
|
(*.9)
|
, где
,
,
как правило, известные параметры
производственной функции, при этом
.