Нелинейное программирование.

Лекция.(случай ограничений неравенств)

• Задачи нелинейного программирования – задачи математического программирования, в которых хотя бы одна из функций нелинейна. В общем случае эти задачи не имеют точных аналитических методов решений. Основные методы их решения – приближенные.

Учет ограничений в форме равенств Прошлая лекция! Учет ограничений в форме неравенств

Наибольшие трудности в нелинейном программировании связаны с учётом ограничений в форме неравенств, например вида .

Такие задачи в общем не решаются, но существуют алгоритмы решения некоторого подмножества задач нелинейного программирования, например, задачи выпуклого программирования.

Задачи выпуклого программирования

• Задачи выпуклого программирования – задачи нелинейного программирования, в которых ищется минимум выпуклой () функции цели, а область допустимых значений выпукла (). Это гарантирует одноэкстремальность задачи и позволяет сформулировать признак оптимальности решения.

• Задачи квадратичного программирования – задачи выпуклого программирования, имеющие квадратичную целевую функцию с линейными ограничениями.

Базовые понятия

Выпуклые множества.

Евклидовым пространством называется множество Х, состоящее из векторов , для которых определены операции сложения, умножения на скаляр, удовлетворяющие всем аксиомам линейного пространства, а также определена двуместная операция ( , ), которая называется скалярным произведением и которая обладает следующими свойствами:

1. знакопостоянна ( , )  0;    ( , ) = 0   =0

2. симметрическая ( , ) = ( , )

3. линейна по первому аргументу

В евклидовом пространстве введено понятие нормы вектора х:

Для нормы выполняются соотношения:

||x||  0    ||x|| = 0 тогда и только тогда, если = 0

||a || = |a| || ||

|| + ||  || || + || ||

Евклидова норма и скалярное произведение связаны между собой неравенством Коши – Буняковского:

( , )  || || || ||

Элемент множества Х называется точкой евклидового пространства.

1. Точка называется предельной, если любая ее окрестность содержит бесконечное число точек того же множества.

2. Множество, содержащее все свои предельные точки, называется замкнутым.

3. Точка называется граничной, если любая ее окрестность содержит как точки данного множества, так и точки, не принадлежащие данному множеству.

4. Множество граничных точек называется границей множества.

Множество Х называется выпуклым если вместе с двумя любыми точками X, Х ему принадлежащими оно содержит и соединяющий их отрезок.

Из X, Х следует z =  + (1–) X        для всех 0    1

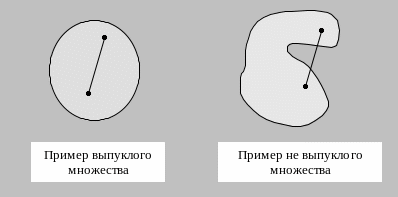
Пересечение любого числа выпуклых множеств – всегда выпукло.

Объединение выпуклых множеств в общем случае может быть и невыпуклым.

Выпуклые функции.

Заменить fi на F!

Функцию F( ), определенную на выпуклом множестве Х, называют выпуклой, если для любых , Х и всех 0    1 выполняется неравенство:

                     (1)

Другими словами, если точка на отрезке, соединяющем точки и , то значение функции в этой точке меньше, чем ордината хорды, соединяющей значения функции и в этих точках

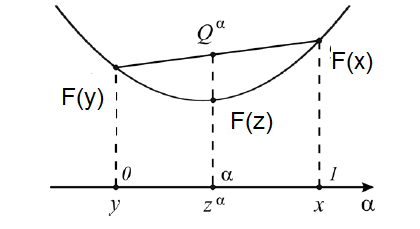
Если неравенство превращается в равенство только при  = 0 и  = 1, то функция называется строго выпуклой.

Картинка из НижнНовгорд_Лобач_mo_in_exercises.pdf

Подправить!

Функцию F( ) называют вогнутой функцией на выпуклом множестве Х, если (– F( )) — выпукла на множестве Х или для нее выполняется неравенство с противоположным знаком:

(2)

Нарисовать вогн!

Свойства выпуклых функций

1. Хорда, соединяющая две любые точки кривой графика выпуклой функции, всегда проходит над кривой в интервале между двумя этими точками.

2. Касательная к графику лежит не выше графика: линейная аппроксимация функции в любой точке интервала всегда позволяет получить нижнюю оценку истинного значения функции.

Теорема. Если выпуклая функция определена на выпуклом множестве Х, то всякая точка локального минимума * является одновременно и точкой глобального минимума.

Критерии выпуклости функции

Тангенс угла наклона касательной или первая производная F( ) возрастает, или, по крайней мере, не убывает при увеличении х.

(F ^|( ) – F ^|( ),   –  )  0

Для выпуклости функции необходимо и достаточно, чтобы ее матрица Гессе была положительно определена (для строго выпуклой функции), или положительно полуопределена (для "невогнутой" функции).

Пример1.

Проще!

И картинку!

Проверить функцию на выпуклость.

f(x, y, z) = 5x² + 5y² + 4z² + 4xy + 2yz

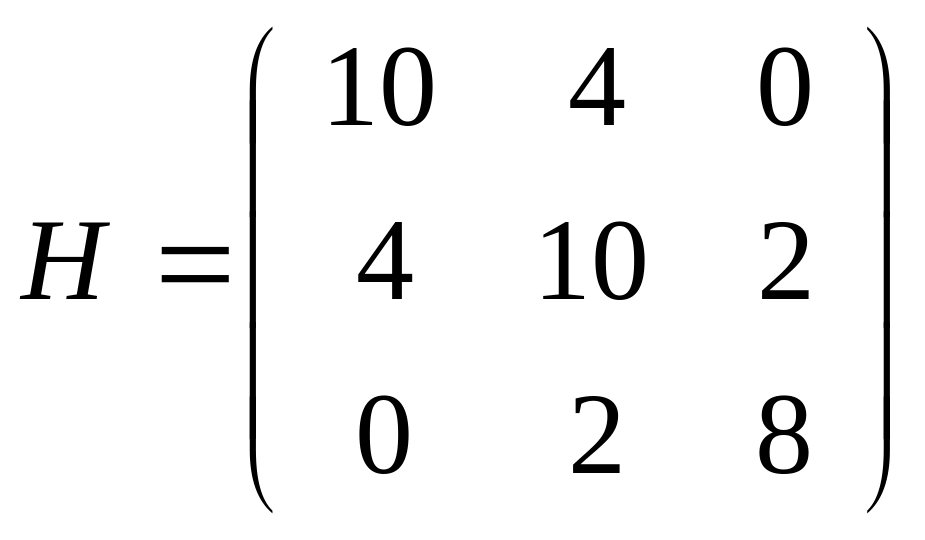
H₁ = 10>0

H₂ = 84>0

H₃ = 632>0

Матрица Гессе положительно определена, значит, функция выпуклая.

Пример2.

Определим, при каких a, b, c функция f(x, y, z) = x² + 2axy + by² +cz² будет выпуклой на Е³

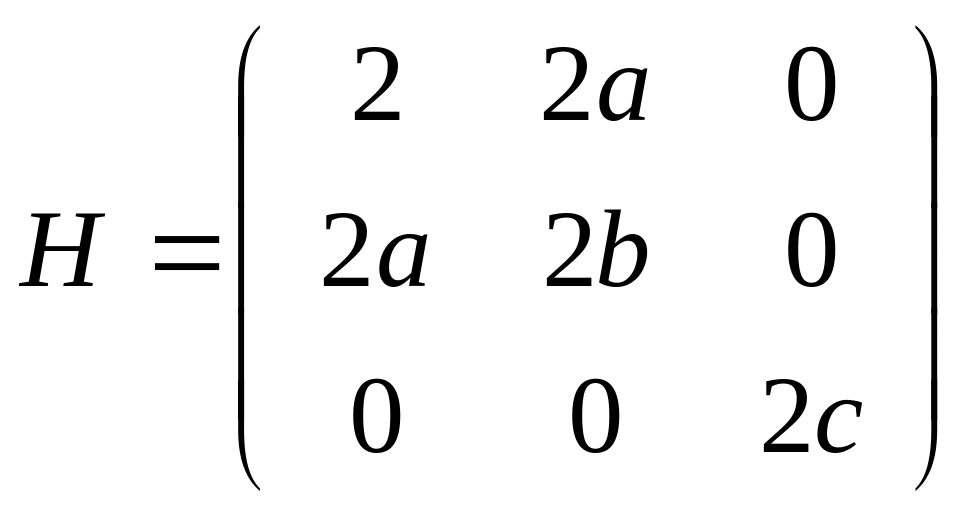
b0, c0, b – a²  0

3) Для любой выпуклой функции ( ), определенной на выпуклом множестве Х, и любого числа  множество

z = {xX; ( )  } — выпукло

или область решения неравенства ( )  , где ( ) – выпуклая функция, является выпуклой.

Пример.

Доказать выпуклость области, заданной следующим неравенством:

x² + y²  16

— положительно определена, т. е. область выпуклая.

Другие свойства выпуклых и вогнутых функций:

          4. Множество точек минимума выпуклой функции, заданной на выпуклом множестве, ‑ выпукло.

5. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки.

6. Если   ‑ строго выпуклая функция, то ее глобальный минимум на выпуклом множестве Х достигается в единственной точке.

7. Пусть функция   ‑ выпуклая функция, заданная на выпуклом множестве Х, и, кроме того, она непрерывна вместе со своими частными производными первого порядка во всех внутренних точках Х. Пусть   – точка, в которой  . Тогда в точке   достигается локальный минимум, совпадающий с глобальным минимумом.

6. Множество точек глобальных (следовательно, и локальных) минимумов выпуклой функции  , заданной на ограниченном замкнутом выпуклом множестве Х, включает хотя бы одну крайнюю точку; если множество локальных минимумов включает в себя хотя бы одну внутреннюю точку множества Х, то    является функцией-константой.