Если
существуют конечные пределы
и
,
то:
2)
3) 
,
в частности,
,
где
4) 
,
в последнем случае предполагается, что
.
Здесь и далее х может стремиться как к конечному числу, так и к бесконечности.
Функция
называется бесконечно
малой
при
,
если
.
Если
,
то
,
где
– бесконечно малая при
.
Пусть
и
бесконечно малые при
,
причем
,
тогда
и
называются эквивалентными
бесконечно малыми.
Обозначение:
при
.
Пусть
,
,
,
– бесконечно малые при
и
,
,
тогда
,
если хотя бы один из этих пределов существует.
Таким образом, при нахождении пределов бесконечно малые можно заменять на эквивалентные им бесконечно малые, более простые.
Часто
используются следующие соотношения
при
:
,
,
,
,
,
,
Первый замечательный предел:
.
Второй замечательный предел:
,
,
где
Пример
2.1.
Найти
.
Решение.
Пределы числителя и знаменателя равны
бесконечности: имеет место неопределенность
вида
.
Чтобы раскрыть эту неопределенность,
разделим числитель и знаменатель дроби
на старшую степень x,
т.е. на x2.
После этого можно применить свойство
3 о пределе частного.
.
Пример
2.2.
Найти
.
Решение.
В данном случае имеем неопределенность
вида
.
Чтобы раскрыть эту неопределенность,
умножим числитель и знаменатель дроби
на выражение, сопряженное числителю,
то есть
на
:
Пример
2.3.
Найти
.
Решение.
Имеем неопределенность вида
.
В числителе и знаменателе перейдем к
эквивалентным бесконечно малым:
,
,
тогда
.
Пример
2.4.
Найти
.
Решение.
Неопределенность
.
Воспользуемся тем, что
при
и получим:
.
Пример
2.5.
Найти
Решение.
Неопределенность вида
.
Применим основное логарифмическое
тождество
,
а потом воспользуемся тем, что
при
.
Тогда
.
§2.2. Непрерывность функции
Функция
называется непрерывной
в точке
,
если
.
Если функция непрерывна в точке , то
,
где – бесконечно малая при .
Все элементарные функции непрерывны в тех точках, в которых они определены.
Точка
называется устранимой
точкой разрыва,
если существует конечный предел в этой
точке и
.
Точка называется точкой разрыва 1-го рода, если существуют конечные пределы слева и справа и
.
Точка называется точкой разрыва 2-го рода, если хотя бы один из односторонних пределов равен бесконечности или не существует.
Пример
2.6.
Функцию
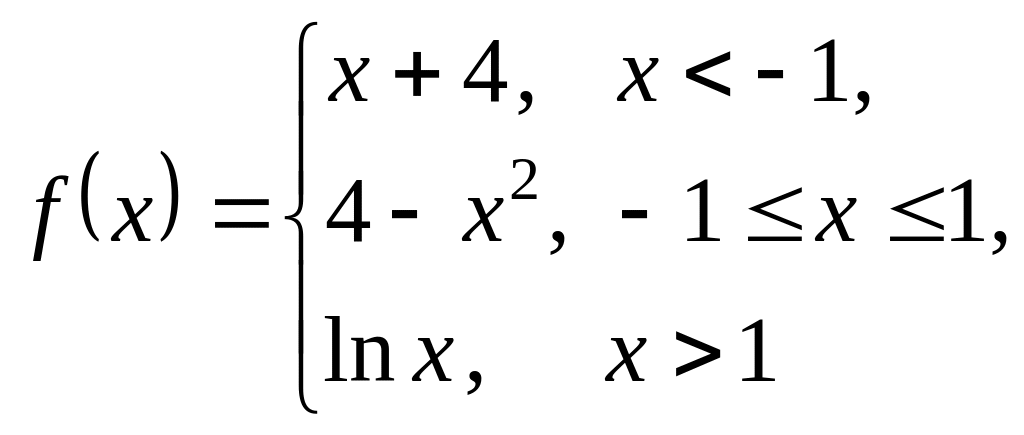
исследовать на непрерывность в точках разрыва и определить их тип. Сделать чертеж.
Решение.
Достаточно проверить непрерывность
этой функции только в точках
и
.
В точке
;
;
;
то есть
.
Следовательно,
функция
непрерывна в точке
.
В точке
;
.
Так как
,
то функция в точке имеет разрыв 1-го рода.
Разность
называется скачком функции в точке разрыва (рис. 17).
Рис. 17.
§2.3. Производная
2.3.1. Определения
Производной
функции
называется предел отношения приращения
функции
к приращению аргумента
,
когда
стремится к нулю:
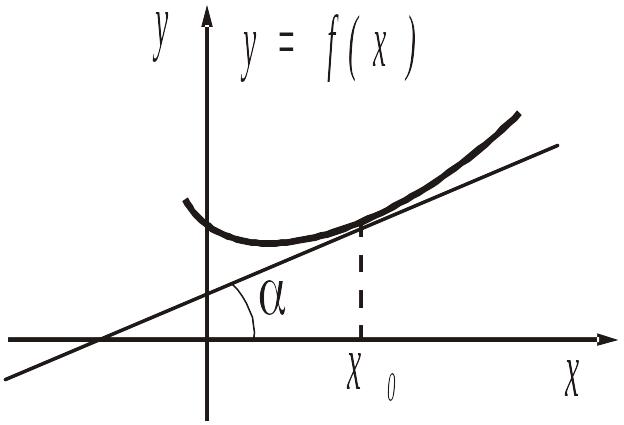
Рис. 18.
Производная
функции
по х
обозначается
или
.
Геометрический смысл производной:
– тангенс
угла наклона
касательной к графику функции
в точке с абсциссой
(рис. 18).
Физический
смысл производной:
–
скорость движения тела в момент времени
t
при прохождении пути
.
Функция, имеющая производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.
2.3.2. Таблица производных
1. |
|
|
8. |
|
2. |
|
|
9. |
|
3. |
|
|
10. |
|
4. |
|
|
11. |
|
5. |
|
|
12. |
|
6. |
|
|
13. |
|
7. |
|
|
|
|
2.3.3. Правила дифференцирования
1. Производная постоянной равна нулю:
.
2. Производная суммы двух функций равна сумме производных этих функций:
3. Производная произведения двух функций:
В
частности,
4. Производная частного двух функций:
5. Производная сложной функции:
если
то
то есть производная сложной функции по независимой переменной х равна произведению производной этой функции по промежуточной переменной u на производную промежуточной переменной по независимой переменной х.
6. Производная обратной функции.
Если
– монотонная непрерывная функция, то
она имеет обратную функцию
(
и
),
и их производные связаны равенством
,
если
.
Пример 2.7. Найти производную функции
Решение. Применим формулы для производной произведения двух функций и производной сложной функции:
Пример 2.8. Найти производную функции
Решение. Применим формулу для производной сложной функции:
.
Пример 2.9. Найти производную функции
Решение. Сначала преобразуем исходную функцию, используя свойства логарифма.
.
Найдём
производную:
