0. 4.2. Оценка точности места методом эквивалентных линий положения.

При предварительных расчетах точности плавания по фарватеру или узкостях, априорная оценка точности обсерваций по n взамонезависимым линиям положения может быть выполнена с помощью калькулятора или компьютера методом эквивалентных линий положения.

Эквивалентные линии положения (ЭЛП) – это линии, проходящие через вероятнейшее место судна и совпадающие с направлениями главных осей эллипса погрешностей (рис. 9).

П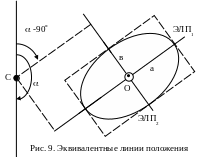 оскольку погрешности места по направлениям главных осей эллипса являются экстремальными, то экстремальными являются и веса эквивалентных линий положения.

СКП первой экстремальной линии положения минимальна и равна в, поэтому вес ЭЛП₁ – максимален – Р_max.

СКП второй линии положения максимальна и равна а, поэтому вес ЭЛП₂ минимален – Р_min.

Между СКП линий положения и их весами существует определенное соотношение ( ). Следовательно, определив веса эквивалентных линий положения можно вычислить и главные полуоси среднего квадратического эллипса:

; (41)

Для нахождения величин р_min и р_max можно выразить коэффициенты нормальных уравнений для взаимонезависимых навигационных параметров через величины ; ; ; .

Тогда

(42)

В данном случае суммируются эквивалентные линии положения. Они взаимно перпендикулярны, поэтому если , то и вместо формул (42) для двух эквивалентных линий положения можно написать:

(43)

Из этого следуют выражения:

(44)

Вместо коэффициентов, стоящих в левых частях данных выражений, подставим их значения, определяемые формулами (42). Тогда после преобразования получим:

(45)

Решив совместно эти уравнения получаем:

(46)

Подставив это в формулы (41), находим полуоси а и в.

Для расчета угла , определяющего направление малой оси эллипса, используется третья формула (39). Подставив в нее значения А₁, А₂ и В₂, получим:

(47)

Номер четверти, в которой расположен угол 2, определяется обычным способом – по сочетанию знаков числителя и знаменателя.

0. 4.3. Графоаналитический способ расчета элементов эллипса погрешностей на основе эквивалентных линий положения.

Расчеты выполняются в следующей последовательности:

1. находится направление _i и величина g_i градиента каждой линии положения.

2. вычисляются веса линий положения:

здесь – погрешность измерения навигационных параметров.

3. вычисляется сумма весов эквивалентных линий положения: она равна сумме весов исходных линий положения:

4. строится полигон весов (квадратичный полигон), для чего на чистом листе бумаги из произвольной точки А (рис. 10) под углом 2₁ к меридиану прокладывается вектор, равный весу первой линии положения; из его конца под углом 2₂ к меридиану прокладывается вектор равный весу второй линии положения, и т.д.; измеряется длина замыкающей полигона весов q (p). Она равна разности весов эквивалентных линий положения.

.

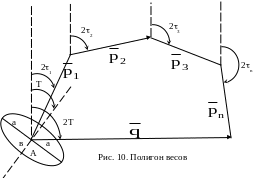
5. Измеряется угол 2Т, который составляет с линией меридиана, замыкающую полигона весов; его половина, т.е. угол Т, представляет собой направление, по которому направлена малая полуось эллипса погрешностей

6. Из уравнений (46) и (41) находятся веса эквивалентных линий положения и величины полуосей эллипса погрешностей обсервованного места судна.

(48)