3. Радиальная погрешность места судна

Для использования эллипса погрешностей необходимо рассчитать три элемента:

а, в и . Это обстоятельство усложняет расчеты и затрудняет сравнение двух или нескольких эллиптических погрешностей.

Более простой и удобной оценкой точности места судна может служить радиальная средняя квадратическая погрешность – радиус круга, проведенного относительно оцениваемого места, равный геометрической сумме главных полуосей среднего квадратического эллипса (рис 7).

(12)

Замена эллипса погрешностей окружностью расширяет площадь нахождения истинного места и, следовательно, вероятность радиальной средней квадратической погрешности больше вероятности среднего квадратического эллипса погрешностей.

В МТ – 2000 есть таблица 4.13 «Вероятность радиальной погрешности». Она служит для определения вероятности Р нахождения места судна в круге заданного радиуса R_Р. Она рассчитана по формуле:

(13)

где – коэффициент (нормированная радиальная погрешность), равный

заданной радиальной погрешности R_Р в долях СКП места ;

– отношение полуосей (большой и малой) среднего квадратического эллипса погрешностей;

­– переменная интегрирования (в угловых единицах)

Значения Р выбираются из таблицы 4.13. по коэффициенту К_Р и отношению полуосей . Если а и в неизвестны, то выборки делают по , что равнозначно выборкам из таблицы 4.15. При вероятности Р соответствуют данным таблицы 4.7 для К_Р = Z.

Решение обратной задачи по определению радиальной погрешности R_Р заданной вероятности выполняются по формуле

(14)

где К_Р – коэффициент, выбираемый по вероятности Р_зад обратным входом из таблицы 4.13 или же непосредственно из таблицы 4.14.

Пример 2. Точность места характеризуется средним квадратическим эллипсом погрешностей с полуосями а = 1,8 мили, в = 0,7 мили. Определить вероятность нахождения места судна в круге радиуса и круге радиуса .

Решение.

1. Рассчитываем отношение полуосей эллипса погрешностей

2. Вычисляем радиальную СКП места судна

3. Для радиальной СКП места , поэтому из таблицы 4.13 по и е = 0.4 получим Р = 0.674

4. Для расчета радиальной погрешности из таблицы 4.13 по и е = 0,4 выбираем Р = 0.881.

Радиальная средняя квадратическая погрешность обсервации, полученной по двум навигационным параметрам рассчитывается по формуле

(15)

при взамонезависимых навигационных параметрах.

Здесь – угол пересечения линий положения.

Если средние квадратические погрешности линий положения выразить через погрешности навигационных параметров и градиенты g то

(16)

Величина М выражается в тех единицах длины, в которых выражены средние квадратические погрешности линий положения (в единицах длины, стоящих в знаменателе размерности градиента).

Из формул (15) и (16) следует, что точность места зависит от угла пересечения линий положения (чем ближе к прямому угол , тем точнее место), от погрешности навигационных параметров (чем меньше эти погрешности, тем меньше М) и от величины градиентов (с ростом градиентов средняя квадратическая погрешность места уменьшается). Если взаимонезависимые навигационные параметры равноточны ( ), то (17)

Если при равноточности навигационных параметров их градиенты одинаковы (высота светил, расстояния), то

(18)

При определении места крюйс – способом первая линия положения смещается по линии пути на расстояние, пройденное судном за время между измерениями навигационных параметров. Следовательно, погрешность первой линии положения усугубляется погрешностью счисления пути на интервале между измерениями параметров, т.е. увеличивается на величину . Поэтому

(19)

Радиальная средняя квадратическая погрешность счислимо – обсервованного места

(20)

При корреляционно взаимозависимых навигационных параметрах (0 <  < 1) радиальная СКП обсервации по двум линиям положения осложняется третьим членом в подкоренном выражении и вместо угла между линиями положения ставится обязательно угол между градиентами навигационных параметров . При этом формула расчета РСКП имеет вид:

(21)

При  < 90 величина cos  положительна, при  > 90 – отрицательна.

Учитывая это, а так же то, что перед третьим слагаемым стоит знак минус, можно заключить, что при положительной корреляции острые углы  предпочтительнее тупых. При  > 90 пренебрежение взаимной корреляцией, т.е. использование формулы (21) без учета третьего слагаемого, приводит к завышению точности обсервации, что в общем случае недопустимо.

Если навигационные параметры содержат существенно преобладающую повторяющуюся погрешность ( = 1), то формула (21) преобразуется к виду , где а₀ – линейная погрешность, вероятность «попадания» истинного места в пределы отрезка от 0 до  а₀ составляет 39,3%, а М – это радиус круга, равный а₀; вероятность попадания истинного места в такой круг составляет 0,683.

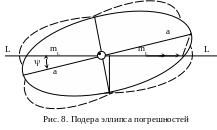
Линейная (одномерная) погрешность места

При решении некоторых задач навигации требуется знать среднюю квадратическую погрешность места судна по заданному направлению – по линии L (например, по направлению на навигационную опасность). Эта погрешность численно равна квадратической сумме проекций главных полуосей среднего квадратического эллипса на заданное направление (рис. 8).

(22)

 – угол между большой осью и линией заданного направления. Концы средних квадратических погрешностей m_L, взятые по всем направлениям, образуют геометрическое место точек, называемое подерой эллипса погрешностей.

При круговом распределении места (рис. 9) линейная средняя квадратическая погрешность по любому из направлений m_L = а = в.

Для радиальной средней квадратической погрешности М линейная СКП по всем направлениям принимается равной

(23)

Линейная СКП соответствует вероятности Р = 0,683.

Линейная погрешность заданной вероятности Р – величина L_P = Zm_L, где

Z – коэффициент функции Лапласа (таблица 4.7 МТ – 2000)

В мореходный таблицах МТ – 2000 для упрощения расчетов линейной СКП есть таблица 4.16 «Коэффициенты для расчета средней квадратической погрешности места по заданному направлению». В таблице формула (22) представлена в виде:

(24)

а – большая полуось среднего квадратического эллипса погрешностей;

– коэффициент, выбираемый из таблицы 4.16 по отношению полуосей от 0,0 до 1,0 и углу от 0 до 180.

Угол  может быть рассчитан по формуле ,

где  – направление большой полуоси эллипса относительно меридиана

_L – заданное направление линейной СКП m_L относительно меридиана.

Если требуется рассчитать линейную СКП по меридиану или по параллели, то в первом случае угол  = , втором –  = 90 - .

При круговом распределении мест (рис. 10) линейная СКП по любому из направлений . Для радиальной средней квадратической погрешности М линейная СКП по всем направлениям принимается равной . Линейная СКП соответствует вероятности Р = 0,683. Линейная погрешность заданной вероятности Р – величина , где Z – коэффициент функции Лапласа (таблица 4.7 – 2000.)