Метод наименьших квадратов (мнк).

Используя метод наименьших квадратов, аппроксимировать табличные данные линейной зависимостью y=ax+b (найти параметры а и b). Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных. Для нахождения коэффициентов составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции по переменным а и b, приравниваем эти производные к нулю.

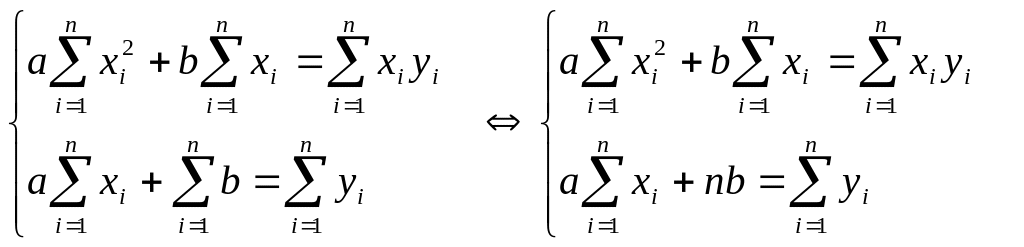Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК). 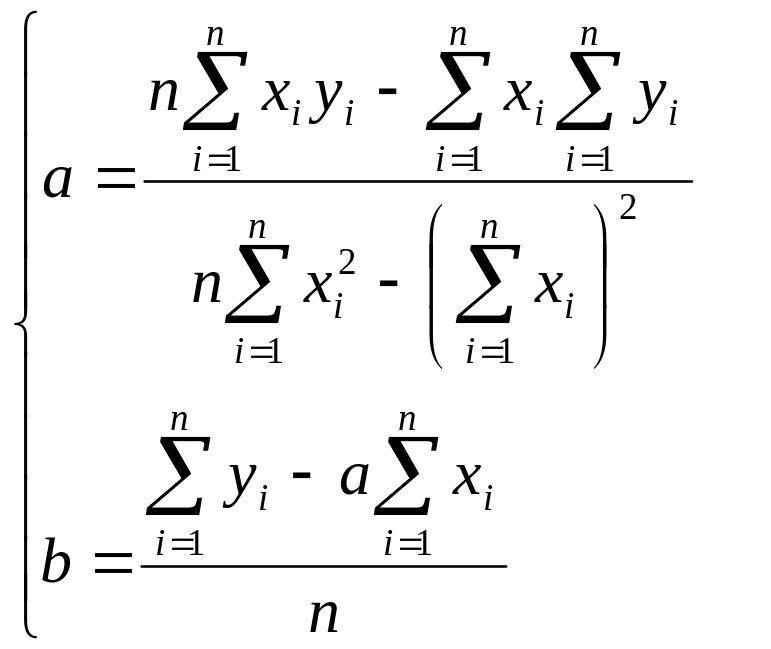При данных а и b функция принимает наименьшее значение. Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы и параметр n - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a. Пример. Экспериментальные данные о значениях переменных х и у приведены в таблице.

	i=1	i=2	i=3	i=4	i=5
xi	0	1	2	4	5
yi	2,1	2,4	2,6	2,8	3,0

Решение. В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов.

i	xi	yi	xi yi
1	0	2,1	0	0
2	1	2,4	2,4	1
3	2	2,6	5,2	4
4	4	2,8	11,2	16
5	5	3	15	25
	12	12,9	33,8	46

Значения в четвертом столбце таблицы получены умножением значений 2-ого столбца на значения 3-его столбца для каждого номера i . Значения в пятом столбце таблицы получены возведением в квадрат значений 2-ого столбца для каждого номера i . Значения последней строчки таблицы – это суммы значений по столбцам. Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы:

Следовательно, y = 0.165x+2.184 - искомая аппроксимирующая прямая. Оценка погрешности метода. Для этого требуется вычислить суммы квадратов отклонений исходных данных от этих линий.

Контрольные вопросы:

1. Выборка. Объем выборки. Варианты и частоты. Вариацион-

ный ряд.

2. Полигон частот дискретного вариационного ряда и гисто-

грамма частот непрерывного вариационного ряда. Эмпирическая функция распределения.

3. Числовые характеристики статистического распределения:

выборочная средняя , выборочная дисперсия , выборочное среднее квадратическое отклонение , исправленная выборочная дисперсия и исправленное выборочное среднее квадратическое отклонение .

4. Что называется инверсией; 2 Что называется конъюнкцией; 3. Что называется дизъюнкцией; 4. Что называется импликацией; 5. Что называется эквивалентностью.

4. Основные понятия теории графов.

5. Алгоритм определения кратчайшего пути.

6. Алгоритм определения критического пути.

7. Сущность метода наименьших квадратов.

5. Оценка параметров уравнения линейной регрессии.