Логические операции и таблицы истинности

1) Логическое умножение или конъюнкция:

Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложное выражение ложно.

Таблица истинности для конъюнкции

p	q	p q
0	0	0
0	1	0
1	0	0
1	1	1

2) Логическое сложение или дизъюнкция:

Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выражения ложны. Таблица истинности для дизъюнкции

p	q	p q
0	0	0
0	1	1
1	0	1
1	1	1

3) Логическое отрицание или инверсия:

Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Таблица истинности для инверсии

p
1	0
0	1

4) Логическое следование или импликация:

Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

Таблица истинности для импликации

A	B	A B
0	0	1
0	1	1
1	0	0
1	1	1

5) Логическая равнозначность или эквивалентность:

Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

Таблица истинности для эквивалентности

A	B	A B
0	0	1
0	1	0
1	0	0
1	1	1

Порядок выполнения логических операций в сложном логическом выражении

1.Инверсия; 2.Конъюнкция; 3.Дизъюнкция; 4.Импликация; 5. Эквивалентность.

Для изменения указанного порядка выполнения логических операций используются скобки.

Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

Пример.

1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:

Переменные		Промежуточные логические формулы					Формула
0	0	1	0	0	1	1	1
0	1	1	1	1	0	1	1
1	0	0	0	1	0	0	1
1	1	0	0	1	0	0	1

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

Оптимизационные задачи на графах

Широкое распространение в задачах управления получили модели в виде графов благодаря дополнительным возможностям, которые появляются при геометрическом подходе к описанию и трактовке процессов управления. Среди графовых моделей особую роль играют потоковые модели, часто называемые транспортными сетями только из-за того, что первоначально они возникли при решении транспортной задачи. К транспортным сетям сводятся многие практические задачи управления, например, задача об оптимальном назначении, о складе, о поставщике, о спросе и предложении, о кратчайшем пути, об оптимальном использовании дорог, об оптимальном по стоимости сетевом графике и другие.

Графом называется пара объектов, состоящая из множества точек и множества отрезков, соединяющих некоторые (может быть, все) из этих точек. Упомянутые точки называются вершинами графа.

Если отрезки, соединяющие вершины графа, имеют направления, то граф называется ориентированным, а сами отрезки – дугами. Если же отрезки не имеют направления, то граф называется неориентированным, и в этом случае говорят, что вершины графа соединены ребрами.

Смешанным называется граф, в котором содержатся как ориентированные, так и неориентированные отрезки. Ориентированный граф часто называют сетью.

Обозначим вершины графа , а дугу, соединяющую вершину c в направлении от к – . Граф Г, образованный множеством вершин Х и множеством дуг U , обозначают Г(Х, U).

Две дуги графа (два ребра) называются смежными, если они различны и имеют общую вершину. Две вершины графа называются смежными, если существует дуга (ребро), соединяющая их.

Говорят, что дуга исходит из вершины , если является ее началом. Дуга заходит в вершину , если является ее концом. Такую дугу мы обозначим через .

Говорят, что в графе данная дуга инцидентна данной вершине, если эта вершина является началом или концом данной дуги.

Обозначим множество дуг, исходящих их данной вершины , а – множество дуг, входящих в . Их объединение есть множество дуг , инцидентных данной вершине.

Представление графа. Граф может быть задан разными способами: рисунком, перечнем вершин и ребер (или дуг) и пр. Одним из самых удобных способов является задание графа с помощью матрицы.

Матрицей смежности графа Г(Х, U) называется квадратная матрица порядка n (n – количество вершин), составленная следующим образом:

.

Другими словами, элемент матрицы , если существует дуга, исходящая из вершины в вершину , и – в противном случае. Для неориентированного графа матрица смежности симметричная.

Матрицей инцидентности называется матрица размера (m – число вершин, а n – число ребер (дуг) графа), определяемая по следующему правилу:

а) для ориентированного графа:

б) для неориентированного графа:

.

Путь в ориентированном графе – это последовательность дуг, в которой конец предыдущей дуги совпадает с началом следующей. Обозначим путь, последовательность вершин которого .

Путь, в котором ни одна вершина не встречается дважды, называется элементарным. Путь, в котором ни одна дуга не встречается дважды, называется простым, в противном случае – составным.

Конечный путь, у которого конечная вершина совпадает с начальной, называется контуром. Контур, образованный одной дугой, называется петлей.

Ориентированный граф называется симметрическим, если любые две смежные вершины его соединены двумя противоположно ориентированными дугами. Ориентированный граф называется антисимметрическим, если каждая пара смежных вершин соединена только в одном направлении и петли отсутствуют.

Для неориентированных графов вводятся понятия, аналогичные понятиям пути, контура и др. Меняются только названия: вместо дуги говорим ребро, вместо пути – цепь, вместо контура – цикл.

Неориентированный граф называется связным, если две любые вершины его можно соединить цепью.

Конечный связный неориентированный граф, не имеющий циклов, называется деревом. Дерево графа, содержащее все его вершины, называется остовом графа или покрывающим деревом. Граф, представляющий объединение деревьев, называется лесом.

В задаче о кратчайшем пути требуется на графе Г найти кратчайший путь – путь наименьшей длины из вершины в вершину .

Алгоритм определения кратчайшего пути.

1. Присвоить каждой вершине метку так, чтобы , = +∞ (для i > 0). Окрасить вершину и положить .

2. Для каждой неокрашенной вершины пересчитать метки по формуле:

.

Если все , то вычисления заканчивают. Задача не имеет решений. В противном случае окрасить вершину, для которой метка минимальна и дугу, ведущую к ней. Положить

3. Если , то кратчайший путь найден. Его длина равна . В противном случае переходят к шагу 2.

Пример Найти кратчайший путь между вершинами s и t для графа, изображенного на рисунке 3.

Решение.

Окрашиваем вершину s. Полагаем , для всех вершин . Имеем:

, , .

Минимальная величина λ для вершины с. Окрашиваем вершину с и ведущую в нее дугу . Полагаем .

Так как вершина t не окрашена, снова пересчитываем метки для неокрашенных вершин:

, , , .

Окрашиваем вершину а и дугу . Полагаем . Пересчитываем метки: , , .

Окрашиваем вершину b и дугу . Полагаем . Пересчитываем метки:

, . Окрашиваем вершину d и дугу (либо дугу ). Полагаем и находим метку .

Окрашиваем вершину t. Кратчайший путь - .

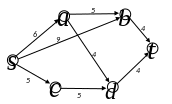Рис. 3.

В некоторых моделях возникает задача о нахождении не самого короткого, а наоборот, самого длинного пути между двумя заданными вершинами графа.

В задаче о критическом пути требуется на графе Г найти критический путь – путь наибольшей длины из вершины X₀ в вершину X_n.

Алгоритм определения критического пути.

1. Присвоить каждой вершине метку так, чтобы , = -∞ (для i> 0).

2. Найти дугу u = u_ij = (X_i, X_j), для которой выполняется неравенство (полагая, что ∞ – ∞ = 0). Заменить метку вершины на новую, большую метку .

3. Пункт 2 применять до тех пор, пока для каждой дуги u_ij не станет справедливым неравенство .

4. Найти вершину X_k, из которой выходит дуга, приходящая в X_n, и для которой ;

затем вершину X_m, из которой выходит дуга, приходящая в X_k, и для которой и т. д. На некотором шаге X_p совпадет с вершиной X₀.

Путь µ = (X_p, … , X_m, X_k, X_n) будет критическим, и его длина будет равна λ_n.