8.5 Задача трёх тел.

Определение движения трёх тел, взаимно притягивающих друг друга с силой, обратно пропорциональной квадрату расстояния между ними, называется задачей трёх тел.

Эта задача очень сложна и её математическое решение трудно. В 1912 году финский математик К. Зундман нашёл формальное решение этой задачи. Он выразил результат в виде степенных рядов. Однако, для расчётов солнечных затмений в рядах Зундмана нужно удерживать число членов, равное примерно единице с 40 нулями.

Лагранж в 1772 году доказал, что существует определённое количество частных случаев в этой задаче, для которых может быть найдено точное решение.

Рассмотрим два из них. В обоих случаях тела описывают подобные между собой кеплеровские орбиты с фокусами в центре масс.

1. Тела образуют лагранжеву конфигурацию - равносторонний треугольник, который может пульсировать в своих размерах и вращаться в своей плоскости в постоянном направлении.

2. Тела образуют эйлерову конфигурацию и находятся на прямой, проходящей через центр масс, и оставаясь на ней, вращаются и пульсируют аналогичным образом. Этот случай был найден Л.Эйлером независимо от Лагранжа в 1767 году.

Е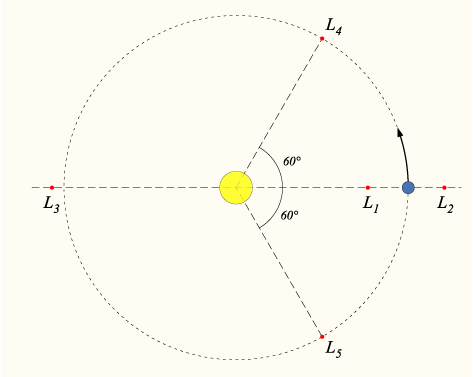 сли заданы массы тел и их положение на плоскости, то рассматриваемые частные случаи движения в этой плоскости получаются при рассмотрении третьего тела в одной из пяти точек, называемых точками либрации или точками Лагранжа.

Первые три точки либрации располагаются в определённых точках прямой, соединяющей обе заданные массы, причём одна между ними, а две другие - вне их. Четвёртая и пятая точки являются вершинами двух равносторонних треугольников, в которых остальные вершины заняты заданными массами.

Лагранж показал, что если третье тело находится в одной из пяти точек либрации, то конфигурация, которую образуют все три тела, всегда остаётся подобной самой себе, а их движение происходит по коническим сечениям одинакового вида.

1. Если тела находятся на одной прямой, то они обращаются, оставаясь на ней, вокруг общего центра масс.

2. Если три тела расположены в вершинах равностороннего треугольника, то они обращаются вокруг общего центра масс так, что треугольник остаётся всё время равносторонним.

В начале ХХ века были открыты две группы астероидов, движение которых соответствует второму решению Лагранжа. В 1907 году был открыт 588 Ахиллес, позднее ещё восемь “греков”, движущихся по соседству с Ахиллесом. Пять “троянцев” движутся с другой стороны. Эти астероиды находятся в точках либрации системы Солнце - Юпитер.

В системе Земля-Луна тоже существуют точки либрации. Эйлеровы называются коллинеарными, а лагранжевы - эквидистантными.

Точки либрации могут быть устойчивыми, лишь когда отношение масс больших тел достаточно мало.

Прямолинейные точки неустойчивы. Достаточно малой возмущающей силы, чтобы либроид удалился из окрестности данной точки. Треугольные точки будут устойчивыми почти для всех достаточно малых отношений масс. Неустойчивость может быть только в двух случаях, когда отношение масс равно одному из двух чисел - 0,0137 и 0,0249.

В 1961 году польский астроном К. Кордылевский наблюдал облакообразные скопления в треугольных точках системы Земля-Луна.

Точки либрации используются в космонавтике.