7.2 Элементы эллиптических орбит.
Движение планеты будет определено, если известны:
- плоскость, в которой лежит её орбита,
- размеры и форма орбиты,
- ориентировка в плоскости,
- момент времени, в который планета находится в определённой точке орбиты.
Величины,
определяющие орбиту планеты, называются
элементами
орбиты.
Плоскость эклиптики является основной
плоскостью, относительно которой
определяется положение орбиты. Д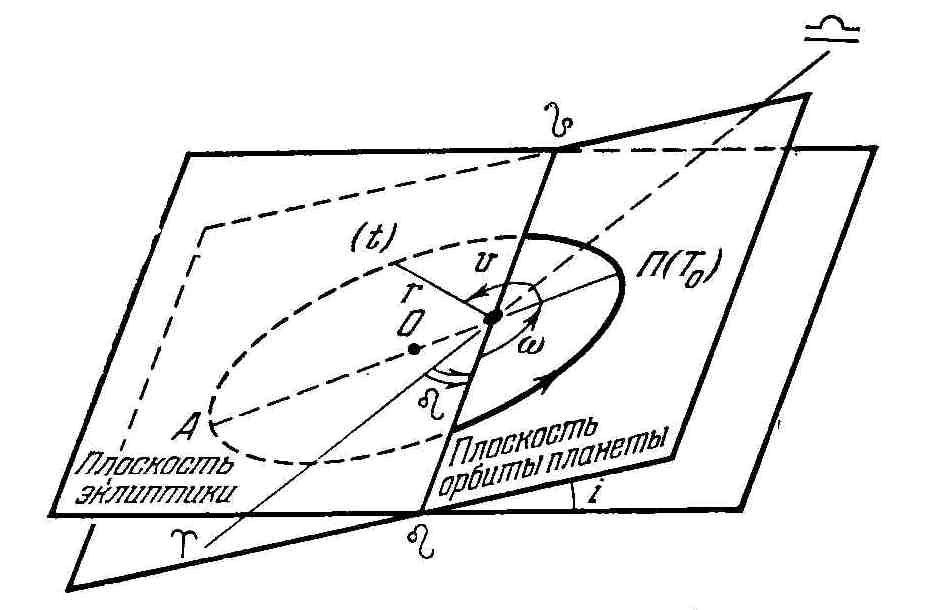
ве
точки, в которых орбита планеты
пересекается с плоскостью эклиптики,
называются узлами
- восходящим и нисходящим.
Восходящий
узел - тот,
в котором планета пересекает эклиптику,
удаляясь от её южного полюса.
Эллиптическую орбиту планеты определяют 6 элементов:
1
Элементы
эллиптических орбит
2. Долгота (гелиоцентрическая) восходящего узла , т.е. угол между направлениями из центра Солнца на восходящий узел и на точку весеннего равноденствия. Долгота может иметь значения от 0º до 360º.
Долгота восходящего узла и наклонение определяют положение плоскости орбиты в пространстве.
3. Угловое расстояние перигелия от узла, т.е. угол между направлениями из центра Солнца на восходящий узел и на перигелий П. Отсчитывается в плоскости орбиты планеты в направлении её движения и может иметь любые значения от 0º до 360º.
Угловое расстояние определяет положение орбиты в её плоскости.
4.
Большая
полуось а эллиптической
орбиты, которая однозначно определяет
сидерический период обращения Т планеты.
Среднее суточное движение n
=
,
т.е. средняя угловая скорость планеты
в сутки.
5.
Эксцентриситет
орбиты е =
,
(1)
где а и b - полуоси эллиптической орбиты. Большая полуось а и е определяют размеры и форму орбиты.
6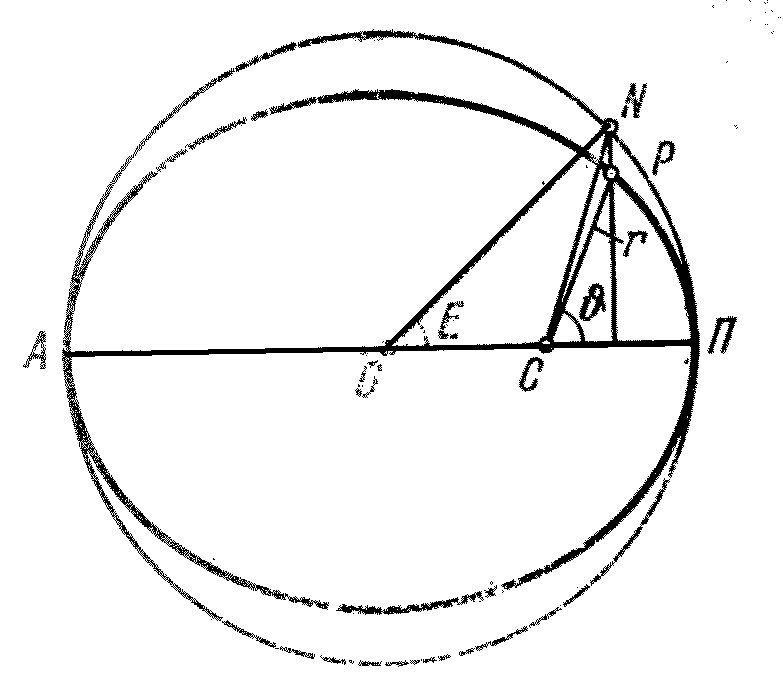
.
Момент прохождения через перигелий t0,
или положение планеты на орбите в
какой-то определённый момент времени
t.
Зная момент прохождения через перигелий t0 и другие элементы орбиты, можно определить положение планеты в плоскости её орбиты для любого момента времени t.
Положение
планеты на орбите определяется двумя
величинами: радиус-вектором
и истинной
аномалией
.
Истинной аномалией планеты называется
угол ПСР между направлением из Солнца
на перигелий П и радиусом-вектором
планеты Р.
r
=
,
(2)
,
(3)
где Е = <ПОN и называется эксцентрической аномалией.
Эксцентрическая аномалия вычисляется из уравнения Кеплера
М = Е - е sin E, (4)
где М - угол, называемый средней аномалией. Средняя аномалия представляет собой дугу круга, которую бы описала планета за время (t - t0), если бы двигалась равномерно по окружности радиуса а со средней угловой скоростью n.
М
= n(t
- t0)
=
.
(5)
7.3 Эфемериды небесных тел
Эфемеридой небесного тела называется таблица, в которой приведены вычисленные на основании теории положения этого тела на небесной сфере для различных моментов времени. При составлении точных эфемерид учитывают возмущения. Приближённые эфемериды составляются на основании известных элементов невозмущённой орбиты данного тела. Определение видимых координат планеты по элементам их орбит называется вычислением эфемерид. Обратная задача, т.е определение элементов орбит по наблюдённым координатам, называется определением орбит. Впервые эту задачу решил Кеплер по многочисленным наблюдениям давно известных планет. В современной астрономии используются методы определения орбит по трём наблюдениям. Эта задача была решена только в 19 веке.
Вычисление положения планеты на орбите для момента t проводится в следующей последовательности:
1) По формуле (5), в которой известны Т и (t - t0), определяют среднюю аномалию.
2) По формуле (4), при известных е и М, методом последовательных приближений находят эксцентрическую аномалию Е;
3) По формулам (2) и (3) вычисляют радиус-вектор и истинную аномалию.
Определив положение планеты на орбите для заданных моментов времени, можно вычислить для этих же моментов её пространственные гелиоцентрические координаты. Зная элементы орбиты Земли и вычислив для тех же моментов положение Земли на её орбите, можно определить геоцентрические координаты планеты и найти её расстояние от центра Земли.