Контрольні запитання

1. Для яких одноканальних СМО можна розв’язати задачі моделювання аналітичним методом?

2. Чим відрізняється моделювання одноканальних замкнутих і розімкнутих СМО?

3. За допомогою яких блоків GPSSW проводиться збір статистичної інформації для каналу обслуговування та для черг?

4. Як перед початком моделювання встановити виведення потрібних параметрів моделювання?

5. Як створену імітаційну модель відкомпілювати і запустити на виконання?

Лабораторна робота 6. Моделювання у GPSS World багатоканальних СМО та оцінка якості їх функціонування

Мета лабораторної роботи – здійснити імітаційне моделювання багатоканальних розімкнутих і замкнутих СМО та провести аналіз ефективності функціонування систем

Загальні відомості

Моделювання багатоканальних розімкнутих СМО. Методи побудови моделей систем з багатоканальними пристроями засобами GPSS World розглянуто у розділі 7. Процес функціонування багатоканальної розімкнутої системи масового обслуговування та основні події, які виникають в процесі роботи такої СМО, зображено на рис. 10.5.

Рис. 10.5. Графічне зображення функціонування багатоканальної розімкнутої системи масового обслуговування

Охарактеризуємо кожну подію, яка виникає в системі, що моделюється.

1. Надходження вимог в систему (GENERATE).

2. Вхід вимоги в накопичувач (ENTER).

3. Визначення каналу обслуговування (TRANSFER).

4. Очікування звільнення одного із каналів обслуговування (SEIZE).

5. Вихід вимоги з накопичувача (LEAVE).

6. Час обслуговування вимоги в каналі обслуговування (ADVANCE).

7. Звільнення каналу обслуговування (RELEASE).

8. Вихід вимоги з системи (TERMINATE).

Вимога по черзі перевіряє всі можливі канали обслуговування до того часу, поки не знайде вільного. Перевагу мають ті канали, які перевіряються першими.

Представимо усі можливі стани досліджуваної СМО у вигляді розміченого графа станів (рис. 10.6). Стан системи визначається числом вимог у ній. Зокрема, можна виділити три варіанти станів:

• у системі немає вимог;

• число вимог n у системі є меншим за число каналів обслуговування (0 < n < N), тобто всі вимоги обслуговуються;

• ч исло вимог n у системі є більшим або рівним за число каналів обслу­го­вування (N ≤ n), тобто N вимог обслуговуються, а очікують у черзі.

Рис. 10.6. Розмічений граф станів системи

Граничні ймовірності станів СМО визначаються із системи алгебраїчних рівнянь:

S_n+1

S_n+1

S_n-1

Процес функціонування багатоканальної замкнутої системи масового обслуговування зображено на рис. 10.7.

Опишемо у контексті блоків GPSS World кожну подію, яка виникає у системі.

1. Надходження вимоги в систему (GENERATE).

2. Вхід вимоги у накопичувач (ENTER).

3. Передача вимоги в один із вільних каналів обслуговування (TRANSFER).

4. Очікування звільнення одного із каналів обслуговування (SEIZE).

5. Вихід вимоги з накопичувача (LEAVE).

6. Час обслуговування вимоги в каналі обслуговування (ADVANCE).

7. Звільнення каналу обслуговування (RELEASE).

8. Повернення вимоги в систему (TRANSFER).

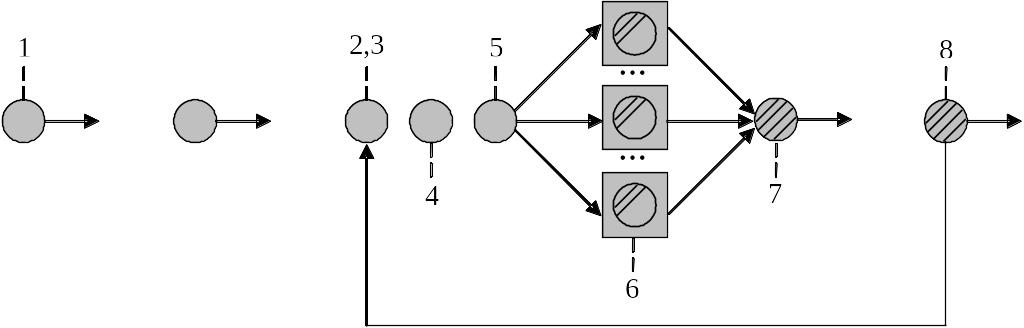
Рис. 10.7. Графічне зображення функціонування багатоканальної замкнутої системи масового обслуговування

Оскільки вимоги з усіх каналів обслуговування повертаються у систе­му, то система є замкнутою. Моделювання таких СМО вимагає генерування обмеженої кількості транзактів (вимог) і відсутності блока для вилучення транзактів з моделі.

П обудуємо розмічений граф станів системи з можливими переходами зі стану в стан (рис. 10.8).

Рис. 10.8. Розмічений граф станів системи

Стан системи пов’язується з числом вимог, що знаходяться у системі. Тут можливі два варіанти:

• кількість вимог n, що надійшли у систему, є меншою за кількість каналів обслуговування (0 ≤ n < N), тобто всі вимоги обслуговуються;

• кількість вимог n у системі є більшою або рівною за кількість каналів обслу­го­вування (N ≤ n), тобто N вимог обслуговуються, а інші очікують у черзі.

Система рівнянь для визначення граничних ймовірностей станів системи має вигляд: