9. Використання plus-процедур для моделювання неперервних систем

Приклад 4. Моделювання системи “Хижак-здобич”

Розглянемо модель Лотка-Волътерра (Lotka-Volterra) або модель “Хижак–здобич” [3]. Нехай на певній території нестримно росте колонія шкідників сільського господарства. Одним із важливих заходів для боротьби зі шкідниками є завезення на цю територію хижаків, які поїдають шкідників. Потрібно визначити, скільки хижаків необхідно завезти, щоб знищити всіх шкідників.

Ця модель описується системою звичайних диференціальних рівнянь. Для моделювання роботи системи “Хижак-здобич” необхідно виділити неперервну й дискретну складові процесу моделювання.

Імітаційну модель “Хижак-здобич” формуємо із трьох секторів. У першому секторі моделюється неперервний процес. У цій частині представимо систему із двох диференціальних рівнянь першого порядку і початкові вихідні дані моделі.

У другому секторі моделюється дискретний процес моделі.

У третьому секторі представимо праву частину системи диференціальних рівнянь моделі за допомогою PLUS-процедур.

Перший сектор моделі:

Hyzhak INTEGRATE (Pryrist_hyzhak())

Zdobych INTEGRATE (Pryrist_zdobych())

Hyzhak EQU 50

Zdobych EQU 800

A_ EQU 0.3000 ;Коеф. народжуваності хижака.

B_ EQU 0.0100 ;Коеф. смерті хижака.

C_ EQU 0.0002 ;Ефективність нападу.

D_ EQU 0.0500 ;Коеф. народжуваності здобичі

Другий сектор моделі може бути представлений у такому вигляді:

GENERATE 2000

TERMINATE 1

Третій сектор моделі може бути представлений у такому вигляді:

PROCEDURE Pryrist_hyzhak() BEGIN

TEMPORARY Din_narodzhennja, Din_smerti, Din_pryrostu;

IF (Hyzhak < 0) THEN Hyzhak = 0;

IF (Hyzhak > 10e50) THEN Hyzhak = 10e50;

Din_narodzhennja = A_ # C_ # Hyzhak # Zdobych;

Din_smerti = B_ # Hyzhak;

Din_pryrostu = Din_narodzhennja - Din_smerti;

RETURN Din_pryrostu;

END;

PROCEDURE Pryrist_zdobych() BEGIN

TEMPORARY Din_narodzhennja, Din_smerti, Din_pryrostu;

IF (Zdobych < 0) THEN Zdobych = 0;

IF (Zdobych > 10e50) THEN Zdobych = 10e50 ;

Din_narodzhennja = D_ # Zdobych;

Din_smerti = C_ # Hyzhak # Zdobych ;

Din_pryrostu = Din_narodzhennja - Din_smerti;

RETURN Din_pryrostu;

END;

Результати моделювання представимо у вигляді графіка. На осі абсцис відкладається час моделювання системи, а осі ординат – чисельність хижаків і здобичі в кожний момент часу моделювання системи.

Дану імітаційну модель необхідно відкомпілювати і запустити на виконання (Command ► Create Simulation).

Для представлення результатів моделювання у графічній формі виконаємо такі команди: Window (головного меню системи) ► Simulation Window (Вікно моделювання) ► Plot Window (Вікно графіка). У діалоговому вікні Edit Plot Window (Вікно редагування графіка) вводиться інформація, як показано на рис. 8.5.

Для розташування у графічному вікні двох графіків заповнюємо діалогове вікно Edit Plot Window у два етапи. На першому етапі, за допомогою клавіші Tab, вводиться наступна інформація в текстові поля:

• у поле Label (Мітка) слово “Здобич”;

• у поле Expression назва шуканої змінної Zdobych;

• у поле Title (Заголовок) текст: “Модель Хижак-здобич”;

• у поле Time Range (Тимчасова область) значення 2000;

• у поле Min Value (Мінімальна величина) залишимо наведене значення без змін;

• у поле Max Value (Максимальна величина) значення 2000.

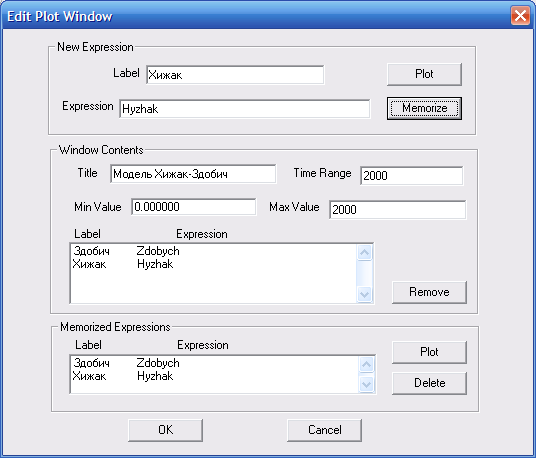
Рис. 8.5. Діалогове вікно Edit Plot Window для моделі “Хижак-здобич”

Активізуємо кнопки Plot (Графік) і Memorise (Запам'ятати). Інформація, введена в перших двох текстових полях, з'явиться у двох нижче розташованих багаторядкових списках.

Таким чином вказується вся необхідна інформація для виведення в графічному вигляді результатів моделювання, що стосуються шуканої змінної Zdobych.

Тепер внесемо всі необхідні дані для виведення в графічному вигляді результатів моделювання шуканої змінної Hyzhak. За допомогою клавіші Tab вводиться інформація в текстові поля, а саме:

• у верхньому полі Label замість слова “Здобич” записуємо “Хижак”;

• у поле Expression замість імені змінної Zdobych вводимо назву змінної Hyzhak;

• активізуємо кнопки Plot і Memorize. Інформація з перших двох текстових полів додається до раніше введених даних у двох багаторядкових списках, розташованих нижче. Натискаємо кнопку ОК. Відкриється вікно PLOTS (Графіки), показане на рис. 8.6, із підготовленим шаблоном графіка.

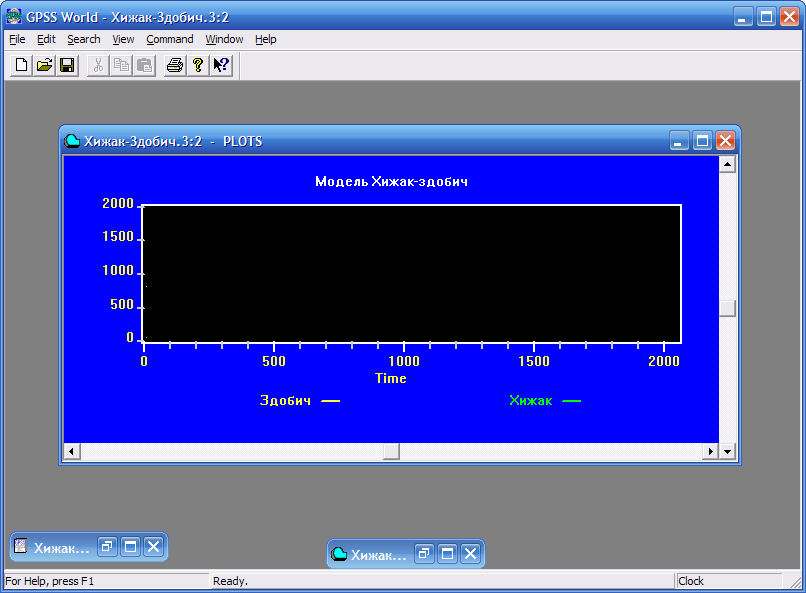
Рис. 8.6. Вікно PLOTS для моделі

Змінити шаблон графіка у вікні PLOTS можна натисканням „мишки” на горизонтальній смузі прокручування графіка ліворуч від бігунка. Тепер можна запустити систему на моделювання: Command ► START► ОК.

Система диференціальних рівнянь, яка наведена в моделі, розв’язуєть­ся методом Рунге-Кутта п'ятого порядку. Результатом моделювання є шукані графіки у вікні PLOTS (рис. 8.7).

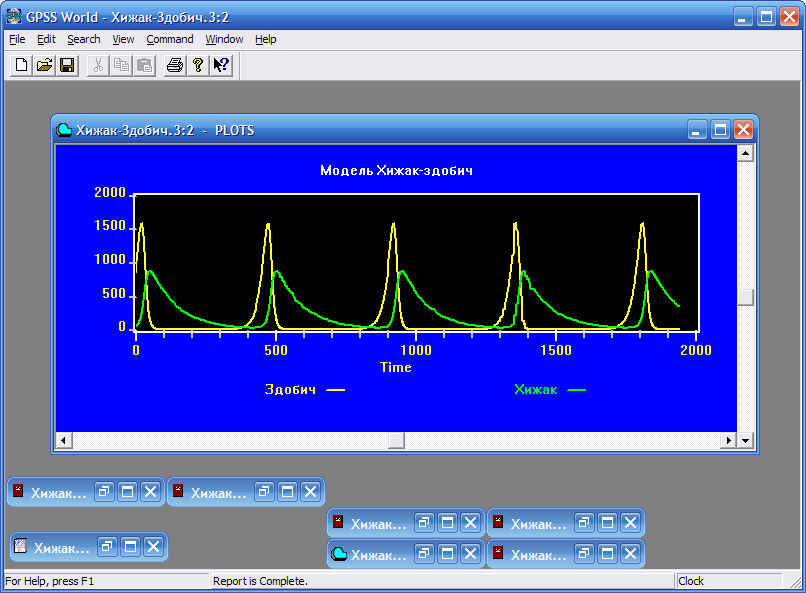
Рис. 8.7. Вікно PLOTS з результатом моделі “Хижак-здобич”

Аналізуючи графічні дані, можна зазначити, що для заданих початкових значень кількості хижаків і здобичі відповідно 50 і 800 максимальне число хижаків і здобичі не перевищує відповідно 900 і 1700 одиниць.

Дана модель дозволяє визначити зміну популяцій хижаків і здобичі для інших вхідних початкових значень. Нехай початкове значення кількості хижаків збільшується з 50 до 80, а початкова кількість здобичі залишається попередньою.

Для цього у вікні Model Window вводимо Hyzhak EQU 80 і закриваємо вікно PLOTS. Виконуємо команди: Command ► Retranslate (рекомпіляція моделі) ► Window (головне меню) ► Simulation Window ► Plot Window. Тепер встановлюємо параметри для графіка. Для цього у діалоговому вікні Edit Plot Window у розділі Memorized Expression (вирази, що запам’ята­лися) вибираємо рядок із шуканою змінною Zdobych і натискаємо кнопку Plot. У цьому ж розділі вибираємо другий рядок із шуканою змінною Hyzhak i натискаємо кнопку Plot. У текстовому полі вводимо попереднє значення 1700, а в текстовому полі Max Value (максимальна величина) вводимо попереднє значення 1700. Далі виконуємо команди: Command ► START ► ОК. Результат моделювання з’явиться у вікні PLOTS з врахуванням зміни початкових параметрів моделі.

Приклад 5. Моделювання поширення епідемії

Нехай у мікрорайоні, населення якого становить 30000 чоловік, виникла епідемія, і з'явилося 50 інфікованих хворих. Припустимо, що приріст хворих за день пропорційний добутку числа здорових людей на число хворих. Коефіцієнт пропорційності Ki (коефіцієнт поширення інфекції) включає різного роду профілактичні заходи, прийняті під час епідемії. Потрібно визначити максимальне число хворих та особливості розвитку епідемії.

Відомо, що процес розвитку епідемії може бути описаний системою двох диференціальних рівнянь:

X_' = X_  (Ki  Y_ – 1);

Y_' = – Ki_  Х_  Y_,

де: Х_ , Y_ – змінні, які описують кількість хворих і здорових людей.

Для моделювання процесу поширення епідемії виділяємо дві частини процесу: неперервний і дискретний.

Результати моделювання представимо у графічному вигляді. На осі абсцис відкладається час моделювання системи, а на осі ординат – число здо­рових і хворих людей у кожний момент часу моделювання системи. Одини­цею виміру часу може бути доба. На рис. 8.8 представлена імітаційна модель процесу поширення епідемії. Параметр Ki є коефіцієнтом поширення інфекції, що залежить від багатьох факторів. Він прийнятий рівним 0,0002. Часовий інтервал процесу моделювання приймаємо рівним 30 добам. Оскільки в процесі інтегрування шукані параметри можуть вийти за допустимі межі, то у PLUS-процесах вводяться відповідні обмеження за допомогою умовного оператора.

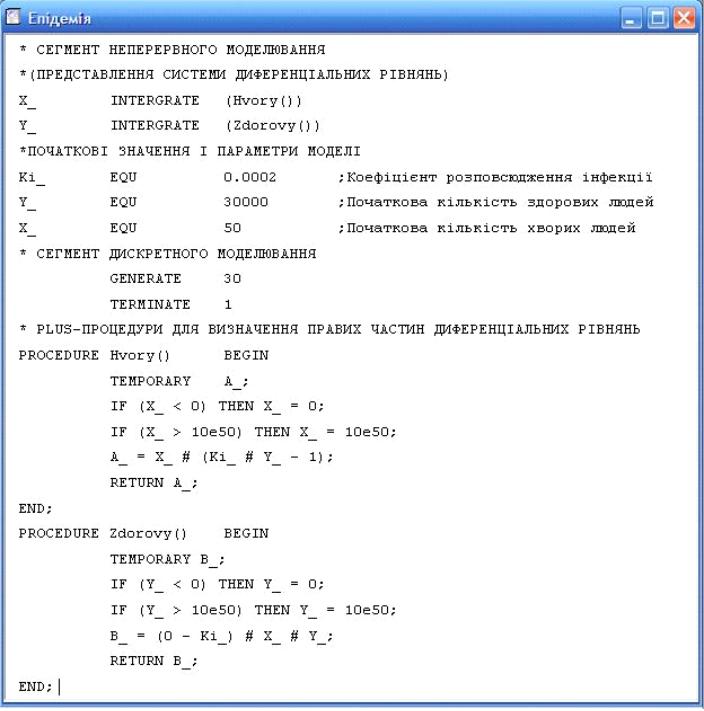
Рис. 8.8. Вікно імітаційної моделі поширення епідемії

Для представлення результатів моделювання у графічному вигляді вико­нуємо команди: Window ► Simulation Window ► Plot Window. Відкриється діалогове вікно Edit Plot Window, у яке вводиться інформація, як показано на рис. 8.9.

Як і у попередньому прикладі, розташуємо два графіки в одному графічному вікні. Заповнення діалогового вікна Edit Plot Window виконуємо у два етапи. На першому етапі вводиться наступна інформація в текстові поля, переміщаючись між ними за допомогою клавіші Tab:

• у поле Label – “Число хворих людей”;

• у поле Expression – назва шуканої змінної Х_;

• у поле Title – “Динаміка епідемії”;

• у поле Time Range – значення 30 (це число діб моделювання);

• у полі Min Value – залишимо наведене значення без змін;

• у поле Max Value – значення 50000 (початкова кількість здорових людей).

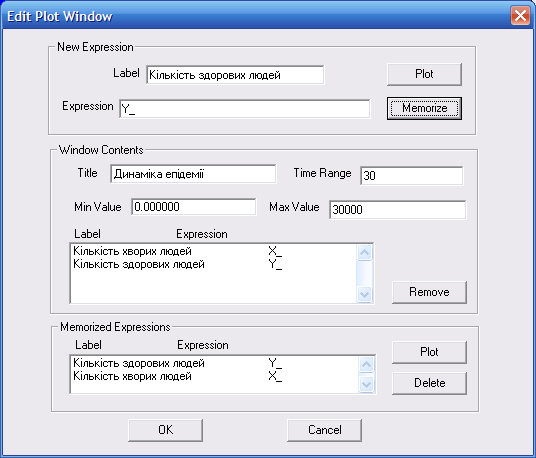
Рис. 8.9. Діалогове вікно Edit Plot Window для моделі поширення епідемії

Активізуємо кнопки Plot і Memorize. Інформація, введена у перших двох текстових полях, з'явиться у двох багаторядкових списках, розташо­ваних нижче. Отже, задана вся необхідна інформація для виведення у графічному вигляді результатів моделювання змінної Х_ .

Для задавання необхідної інформації для виведення в графічному виді результатів моделювання шуканої змінної Y_ вводиться наступна інформація в текстових полях:

• у поле Label “Число хворих людей” замінюємо на “Число здорових людей”;

• у поле Expression замість назви шуканої змінної Х_ вводиться назва шуканої змінної Y_.

Далі активізуємо кнопки Plot і Memorize. Дані, зазначені в перших двох текстових полях, додадуться до раніше уведеної інформації у двох багаторядкових списках, розташованих нижче. Натискаємо кнопку ОК. Відкриється вікно PLOTS із шаблоном графіка (рис. 8.10).

Рис. 8.10. Вікно PLOTS для моделі поширення епідемії

Тепер запускаємо систему на моделювання. Розв’язання системи дифе­ренціальних рівнянь, наведеної в моделі, отримується методом Рунге-Кутта п'ятого порядку. Результати моделювання показані у вікні PLOTS (рис. 8.11).

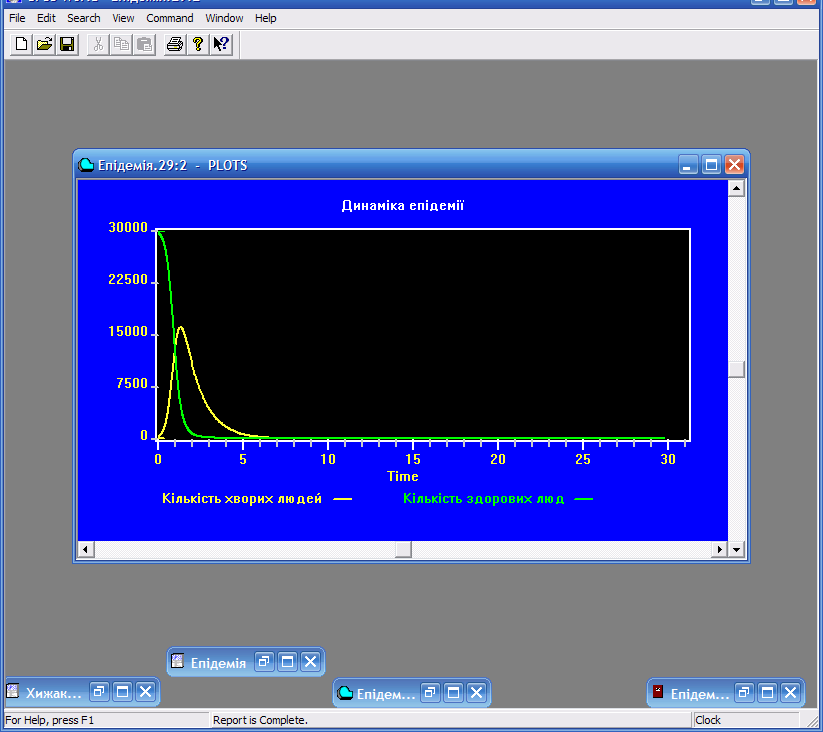
Рис. 8.11. Вікно PLOTS з результатами моделювання поширення епідемії

Аналіз отриманих результатів свідчить про те, що для заданих початкових значень – кількості здорових людей 30000 і хворих 50 кількість хворих досягне максимуму через 2 доби і складе близько 17000 чоловік.

Моделювання процесу поширення епідемії для інших початкових значень моделі здійснюється виконанням аналогічних команд, описаних у попередньому прикладі. Нехай початкове значення коефіцієнт та поширення епідемії становить 0,0004, тобто

K_і_ EQU 0,0004

Закриваємо вікно PLOTS і виконуємо команди: Command ►Retranslate ► Window ► Simulation Window ► Plot Window. У розділі Memorized Expression вибираємо рядки:

Число хворих людей Х_

Число здорових людей Y_.

Після вибору кожного рядка натискаємо кнопку Plot. У текстове поле Time Range вводимо значення 30, а в текстове поле Max Value записуємо попереднє значення 30000. Після виконання команд Command ► START ► ОК у вікні PLOTS з’являються нові результати моделювання (рис. 8.12).

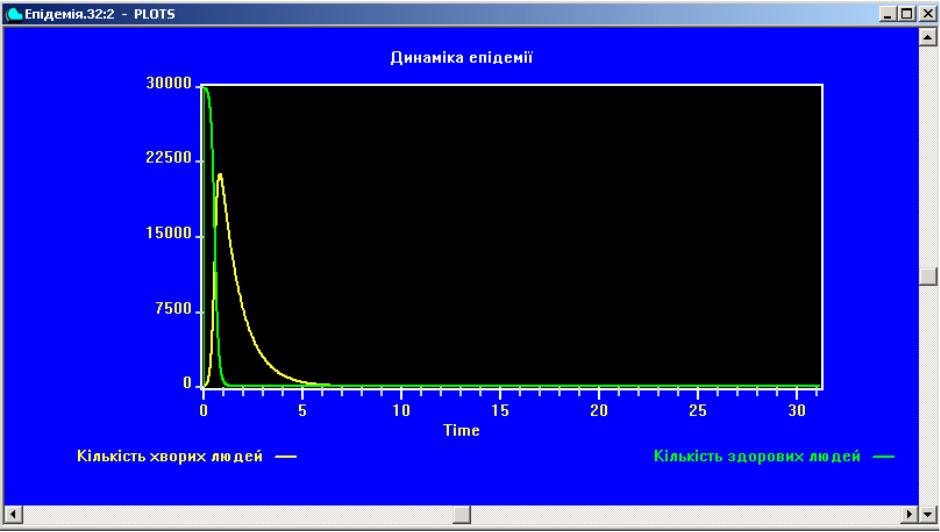
Рис. 8.12. Результати моделювання процесу поширення епідемії після зміни коефіцієнта Kі_ на 0.0004