6.3 Розрахунок ціни шляхом аналізу граничного її рівня

Як показує світова практика, для найбільш точного визначення і глибокого аналізу споживної вартості випускного продукту необхідне використання такого показника, як гранична ціна. У сучасних умовах під нею розуміють рівень ціни розглянутого устаткування, при призначенні якого покупець, який придбає досліджувану машину, не одержує абсолютно ніяк переваг у порівнянні з придбанням машини-аналога [75]. Під останнім розуміється той продукт, вироблений конкуруючої фірмою, який має принципово точно відповідати досліджуваному устаткуванню за своїм призначенням. Однак, обраний аналог має бути не абстрактним продуктом (товаром-ідеалом, що символізує існуючу потребу), а машиною, ринкова ціна і технічні характеристики якої мають бути свідомо відомі. Крім того, незважаючи на ідентичність призначення, обоє розглянутих товарів, як машина-аналог, так і аналізоване устаткування, мають функціональні і класифікаційні показники конкретно заданого рівня, які можуть істотно відрізнятися. З попереднього очевидно, що при подальшому збільшенні ціни після подолання рівня граничної досліджуване устаткування стає неконкурентоспроможним.

Крім того, що особливо важливо, показник граничної ціни дозволяє об'єднати в собі інтереси обох зацікавлених сторін, як споживача, так і виробника. З погляду продуцента в поняття ціни вкладається зміст вартості матеріальних і інших ресурсів, які витрачаються на створення машини і, виходячи з цього, чим вище зазначені витрати, тим вище рівень ціни.

Так виглядає ідеальна ситуація ціноутворення з позиції виробників, до якої кожний з них прагне. Для цього як найбільше ємний показник, максимальним чином характеризуючий ціну, заведено вважати «масу устаткування», тому що вона враховує величину всіх згаданих вище ресурсів.

Що стосується споживача, то з його погляду процес ціноутворення виглядає трохи інакше, у результаті того, що він, придбаючи машину, платить не просто за сукупність ресурсів, вкладених у неї виробником, а за ті можливості, що йому ці ресурси, втілені в покупне устаткування, надають, тобто, інакше кажучи, за виконувані їм функції, сукупність яких характеризується визначеними групами показників, а саме, класифікаційними, функціональними і показниками призначення. Таким чином, на даний момент маємо справу з абсолютно різними позиціями, навіть можна з упевненістю сказати, що ці точки зору прямо протиставляються один одному.

Виходячи з цього, з метою перебування загальної точки зіткнення у сфері ціноутворення інтересів споживача і виробника, тобто компромісного рішення проблеми, що створилася, необхідне виведення показника чи групи показників, який міг би відбити позиції обох сторін. Таким показником була обрана маса устаткування [13], у результаті того, що вона, як і ціна машинобудівної продукції має функціональну залежність з показниками призначення.

Викладене вище було запропоновано авторами [13] подати в аналітичному виді:

, (6.6)

де Ц - гранична ціна устаткування;

М - маса машини;

F₁ - функція залежності ціни устаткування від його маси;

F₂ - функція залежності ціни устаткування від класифікаційних і функціональних показників призначення;

F₃ - функція залежності маси устаткування від класифікаційних і функціональних показників призначення.

У залежності від того, для якого виду устаткування проводиться аналіз, показники формули (6.6) беруть відповідні індекси і тоді формула (6.6) для аналізованого устаткування і машини-аналога набуває наступного виду:

У випадку ідеальних економічних відносин, при яких усі виробники мали б однакові умови виробництва і вели б конкурентну боротьбу, яка являє собою суперництво за найбільш комфортні, своєчасні умови постачання товару споживачу, а, крім того, направляли бы свою діяльність на конкретну вузьку групу споживачів, тобто працювало б в одному сегменті, пропонуючи їм ідентичну за своїми класифікаційними і функціональними показниками продукцію, спостерігалася б ситуація, описувана наступною рівністю

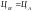. (6.9)

Однак, у дійсності це не досяжно, у результаті чого, виникає протиріччя між пропозицією виробника і попитом споживача, який полягає в тому, що покупець не займається порівнянням умов виробництва, а віддає перевагу тим товарам, споживча вартість яких його влаштовує. Тому що останній показник у різних виробників звичайно не збігається в результаті різних умов виробництва, неоднорідності використовуваних сировини, матеріалів і комплектуючих виробів, а також під впливом інших факторів, то це позначається як на рівні якості, технічному рівні виробленої продукції, так і на споживчій вартості, що є причиною наступної нерівності:

. (6.10)

З метою відновлення рівності між двома цими показниками необхідно праву частину нерівності (6.10) помножити на поправковий коефіцієнт, тоді формула (6.10) набуде відповідного виду

. (6.11)

Поправковий коефіцієнт (К), у свою чергу, являє собою відмінність ціни досліджуваного устаткування (у функціональному уявленні) і машини-аналога у відносному вираженні

. (6.12)

Якщо врахувати існування функціональної залежності, описаної вираженнями (6.7) і (6.8), то рівняння (6.12) буде подано в такий спосіб:

. (6.13)

Підставивши вираження (6.13) у рівняння (6.11), одержимо функціональну залежність ціни досліджуваного устаткування і машини-аналога:

, (6.14)

де Ц_и^пред. - величина граничної ціни досліджуваного устаткування.

Як вказують автори формули (6.14) [75], недостатньо множення ціни машини аналога на поправковий коефіцієнт, тому що для більш точного визначення граничної ціни досліджуваного устаткування, поряд з обговореними раніше закономірностями необхідно враховувати ще і той факт, що ціна, яку «споживач готовий платити за устаткування виробничого призначення за інших рівних умов прямо пропорційна віддачі (Qекс_.), яку він (споживач) від цього устаткування очікує одержати» [75]. Таким чином, для визначення досліджуваного показника необхідно враховувати і різницю між технічним рівнем досліджуваної машини й аналога. У відносному вираженні експлуатаційна продуктивність (Qекс_.) визначається з використанням формули (7.17), тобто на підставі основного рівняння функціонування устаткування.

Для коректування рівняння (6.14) необхідно знайти відношення розрахункових величин експлуатаційних продуктивностей (Qекс_.) досліджуваного устаткування і машини-аналога. Ця дія виробляється з метою запобігання подвійного обліку тих самих показників, у результаті того, що всі необхідні класифікаційні і функціональні показники призначення, що впливають на економічну сторону, уже враховані у вираженні (6.14), однак, у ньому упускається означена прямо пропорційна залежність ціни від експлуатаційної продуктивності (Qекс_.). Таким чином, уведене відношення є ще одним поправковим коефіцієнтом:

, (6.15)

де К_попр. - поправковий коефіцієнт, що враховує відмінність експлуатаційних продуктивностей досліджуваного устаткування і машини-аналога.

Щоб уникнути неточності розрахунків, потрібно виявити акуратність при визначенні експлуатаційної продуктивності обох видів устаткування, щоб ні в якому разі не врахувати показники, які не мають ніякого відношення до характеристик даного устаткування.

Якщо врахувати усі зазначені виправлення, то гранична ціна досліджуваного устаткування теоретично обґрунтовано може бути визначена за формулою (6.16) [75]:

. (6.17)

Виходячи з тверджень існуючої методики [75], маса будь-якого устаткування знаходиться у функціональній залежності від класифікаційних і функціональних показників призначення, а саме лінійних, силових, теоретичних, продуктивних та інших, і виражається функцією F₃.

Таким чином, на даному етапі основною задачею є визначення і виведення вказаної вище функції.

Аналіз публікацій, спрямованих на визначення маси різних видів устаткування через виведення її функціональної залежності від функціональних і класифікаційних параметрів призначення, свідчать про незаперечний факт, що багатьом авторам [12;55] удалося досягти поставленої мети шляхом побудови шуканої функції через мультиплікативне вираження, що, крім теоретичної обґрунтованості, забезпечує ще і досить високу відповідність розрахункових результатів до практичних спостережень, що говорить про максимальну придатність даного методу для використання в реальних виробничих умовах.

Спираючись на досвід попередніх авторів, основна мета подальшої роботи має бути спрямована на побудову в мультиплікативній формі емпіричної залежності. Однак, перш, ніж приступити до цього процесу, необхідно зробити істотне зауваження, яке полягає в тому, що найбільш вагомі показники призначення, які роблять істотний вплив на масу устаткування (М), незалежно від його класу й виду, можуть бути виявлені тільки на етапі остаточного визначення емпіричної формули, то найбільш компетентні дослідники в даній сфері наукової діяльності радять проводити аналіз цієї залежності спочатку в загальному виді, не прив'язуючи його ні до якого-небудь конкретного устаткування. Виходячи з цього, вищевказана формула в мультиплікативній формі має наступний вид [92]:

, (6.17)

де К_М - коефіцієнт пропорційності, який визначає вплив якості виконання проекту на масу устаткування;

Z₁,...,Z_n - показники ступеня, інакше називані коефіцієнтами регресії, які визначають вагомість впливу відповідних показників призначення на масу досліджуваного виду устаткування.

За свідченням групи авторів під керівництвом С.А.Айвозяна, процес визначення емпіричних залежностей, у тому числі і розглянутого виду, здійснюється протягом семи, виконуваних у точній послідовності, етапів [2]. На початковому етапі, насамперед, необхідно визначити кінцеву прикладну мету, для якої й організоване виконання всіх намічених робіт. На момент, коли реалізовані цілі поставлені, а виконавцям зрозуміла суть виконуваних задач, є можливість переходу до другого етапу, що складається в зборі статистичних даних та інформації, необхідних для виконання поставлених цілей і проведення необхідного аналізу. Наступним етапом є проведення кореляційного дослідження, що дозволяє виявити існування хоча б якогось зв'язку, навіть незначно вираженим, між досліджуваними величинами, що відразу ж на первісній стадії аналізу дозволить переконатися і визначитися, що виконувані роботи мають теоретичну основу та математичний фундамент. Якщо такий зв'язок знайдений, то на четвертому етапі можна переходити до опису класу функцій, у рамках яких буде здійснюватися подальший пошук і дослідження залежностей. По-п'яте, аналізується мультиколініарність змінних і виробляється добір тих з них, які є найбільш інформативними. По-шосте, виконується оцінка невідомих параметрів, які входять до досліджуване рівняння статистичного зв'язку. І, у результаті, при підбитті підсумків проведеного процесу необхідно проаналізувати точність отриманого рівняння. У випадку недостатньої точності, чи невідповідності до її необхідної величини, необхідно переглянути весь процес ще раз з метою виявлення помилок. Однак, якщо і вони не виявлені, то тоді вводиться поправковий коефіцієнт, який перекриває погрішність розрахунків [41].

Порядок прямого пошуку стосовно, наприклад, до побудови емпіричної формули полягає в наступному. Спочатку потрібно вибрати для кожного з параметрів А, B,C,D початкові передбачувані значення Z1, Z2,..., Zn разом з деяким початковим збільшенням DDZ. Потім за статистичними даними з урахуванням обраних значень Z1, Z2, . .., Zn за наступною формулою визначаються величини Kмi і розраховується коефіцієнт варіації:

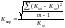, (6.18)

де Км - середнє значення Кмi за виборкою розглянутої бази даних;

m - кількість кранів у вибірці.

Наступним кроком є заміна якого-небудь значення Zi з набору Z1, Z2, ..., Zn на величину (Zj + DDZ) і, відповідно, визначення нового значення Квар. Якщо значення Квар не зменшиться, іспиту піддається величина (Zj - DDZ). В остаточному підсумку, за мінімумом коефіцієнта варіації визначається деякий локальний оптимум.

Описаний процес повторюється за визначеним алгоритмом для кожного з параметрів окремо, а також для сполучення цих параметрів, що складає серію спробних кроків. Нові оцінки параметрів Z1, Z2,..., Zn утворять деякий вектор у просторі параметрів, що задає напрям, який зменшує Квар. Уздовж цього напряму здійснюється ряд робочих кроків доти, поки при будь-якій зміні значень Z1, Z2, . . . , Zn зменшення величини коефіцієнта варіації виявиться неможливим. У межах, близьких до оптимуму, для більшої точності величина DDZ може бути зменшена. Неможливість подальшого скільки-небудь істотного зниження значення Квар при малих DDZ указує на те, що досягнутий оптимум.

Стосовно вибору початкового збільшення відзначимо, що Д. Химмельблау [104] вважає вибір DDZ=0.3 розумним компромісом між занадто великим початковим розміром кроку, який доведеться, можливо, зменшити перш, ніж почне зменшуватися величина Квар, і занадто малим розміром кроку, що може призвести до великих витрат часу, тому що буде потрібно зробити дуже багато малих кроків.

Для виключення можливості перебування помилкових оптимумів можна порекомендувати проводити описаний процес неодноразово, щораз задаючи нові, істотно відмінні, початкові значення Z1, Z2, ..., Zn.

До достоїнств даної методики визначення функціональної залежності можна віднести найбільш високу точність у порівнянні з іншими способами, легкість опису, а, у випадку, застосування програмного пакета та швидкість проведення процесу.

Методом, аналогічним визначення функціональної залежності маси устаткування від його показників призначення, є можливість виведення рівняння, яке описує залежність ціни устаткування від його маси, тобто функцію F₃ формули (3.19), виходячи з цього F₃ набуде виду

, (6.19)

де х - показник ступеня (коефіцієнт регресії), який визначає вагомість впливу маси устаткування на його ціну;

К¢ў _м - коефіцієнт пропорційності, який визначає вплив величини маси на ціну устаткування.

Таким чином, одержимо остаточний вид даного вираження, яке можна використовувати для будь-якого класу устаткування [75]:

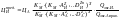. (6.20)

Виходячи з наведених вище доводів, можна зробити висновок про те, що рівняння (6.20) є в даний час найбільш зручним для опису економічної сторони досліджуваного устаткування, тому що воно відбиває не тільки ціну машини, але і показує ступінь впливу найбільш важливих показників призначення на її рівень, а також значущість якості та надійності машини при проведенні процесу ціноутворення. Крім того, даний показник дозволяє в одному рівнянні зробити відповідним і порівнюваний вид продукцію різних фірм.