Задание 8
На основе рассчитанного в п. 6 коэффициента детерминации определить эмпирическое корреляционное отношение и охарактеризовать тесноту корреляционной связи.
Эмпирическое корреляционное отношение рассчитывается по формуле:
В задании 6 был рассчитан коэффициент детерминации:
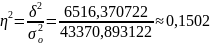
Тогда,
Вывод: связь умеренная (по шкале Чеддока).
Задание 9
По графику эмпирической линии регрессии подобрать форму взаимосвязи факторного и результативного признаков.
Определить параметры и построить уравнение парной регрессии; обосновать возможность использования полученной модели, рассчитав показатели ошибок коэффициента регрессии и уравнения регрессии.
В случае, если подходящая модель носит линейный характер, определить линейный коэффициент корреляции и дать оценку его существенности.
С экономической точки зрения интерпретировать уравнение регрессии, используя коэффициент регрессии, -коэффициент и коэффициент эластичности.
Построенный график эмпирической линии регрессии напоминает прямую, следовательно связь линейная и описывается уравнением
.
Параметры данного уравнения можно рассчитать по формулам:
Найду все переменные в b отдельно:
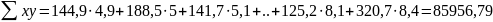
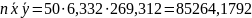
Итак, уравнение связи имеет вид:
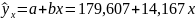
Для того чтобы обосновать, можно ли использовать найденную модель, найдем процентное отношение средней квадратической ошибки уравнения к среднему уровню результативного признака:
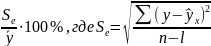
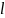– число параметров в
уравнении регрессии (равно 2)
фактические
значения результативного признака
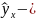значения результативного признака,
рассчитанные по уравнению регрессии
Составлю таблицу со значениями
и
по ним рассчитаю
.
-
y
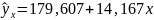
144,9
249,0253
188,5
250,442
141,7
251,8587
207,7
251,8587
1192,1
253,2754
167,1
254,6921
271,1
254,6921
361
256,1088
143,5
256,1088
233,3
256,1088
273,1
256,1088
170
256,1088
191,7
257,5255
419,5
257,5255
234
258,9422
173,7
258,9422
215,5
258,9422
186,6
260,3589
264,2
261,7756
294,2
261,7756
351,3
261,7756
150,8
263,1923
191,8
264,609
178,5
264,609
220,8
264,609
234
266,0257
139,4
267,4424
120,3
268,8591
305,2
268,8591
485
270,2758
223,1
270,2758
299
270,2758
139,1
271,6925
152,9
273,1092
227,1
277,2593
280
277,2593
223
278,776
151,7
280,1927
268,8
280,1927
243,8
284,4428
329
288,6929
1203,3
288,6929
258,8
290,1096
168,5
291,5263
119,9
291,5263
159,2
291,5263
217,3
291,5263
504,7
292,943
125,2
294,3597
320,7
298,6098
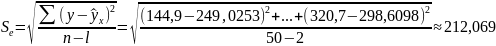
Так как отношение превышает 10-15%, то уравнение регрессии недостаточно хорошо отображает изучаемую взаимосвязь.
В случае, если подходящая модель носит линейный характер, определить линейный коэффициент корреляции и дать оценку его существенности.
Линейный коэффициент корреляции находится по формуле:
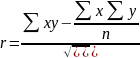
Так как коэффициент корреляции примерно равен 0,07, то связь слабая.
Для определения существенности линейного коэффициента корреляции необходимо найти величину средней квадратической ошибки коэффициента корреляции по формуле:
Полученная величина с
табличным значением t-критерия Стьюдента.
При
.
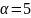
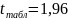Поскольку
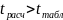коэффициент корреляции считается
значимым.
Вывод: с вероятностью 95% можно утверждать, что связь между уровнем безработицы и средним ВРП на душу населения прямая и слабая.
С экономической точки зрения интерпретировать уравнение регрессии, используя коэффициент регрессии, -коэффициент и коэффициент эластичности.
Найденное уравнение линейной регрессии
имеет вид:
Коэффициент регрессии
b =
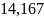показывает среднее изменение
результативного показателя (в единицах
измерения у) с повышением или понижением
величины фактора х на единицу его
измерения.
Коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится значение среднего ВРП на душу населения от своей средней величины при изменении фактора x (уровень безработицы) на 1% от своего среднего значения.
Он находится по формуле:
–
коэффициент
показывает, на какую
часть величины своего среднего
квадратического отклонения изменится
в среднем значение результативного
признака при изменении факторного
признака на величину его среднеквадратического
отклонения.
Бета-коэффициент рассчитывается по формуле:
