Задание 3

Проверить однородность совокупности по показателю «Уровень безработицы» и исключить аномальные единицы совокупности, используя правило «трех сигм».

Правило трёх сигм заключается в том, что 99,73 % значений нормально распределённой случайной величины лежат в интервале (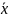 - 3 , + 3σ) .

Среднее арифметическое для уровня безработицы находится по формуле:

Итак,

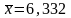
Среднее квадратическое отклонение равно корень из дисперсии. Находим его:

Среднее квадратическое отклонение равно 0,84112.

Подставляем найденные значения в интервал ( - 3 , + 3σ):

В таблице все значения уровня безработицы соответствуют найденному интервалу, поэтому аномальные единицы совокупности отсутствуют.

Для того чтобы проверить однородность совокупности, найдем коэффициент вариации ν.

Итак, .

Следовательно, совокупность является однородной, так как коэффициент вариации не превышает 33 %.

Задание 4

По оставшимся данным построить ряд распределения субъектов РФ по показателю «Уровень безработицы» с равными интервалами.

Нахожу количество интервалов по формуле Стерджесса: (n – число пунктов в таблице).

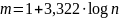
Далее рассчитываю длины интервалов по формуле:

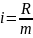, где R – размах, разница между максимальным и минимальным значениями.

Итак,

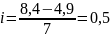
На основе этих данных получаем ряд распределения из семи интервалов:

Уровень безработицы за 2012 г., в %	Число регионов
4,9 – 5,4	7
5,4 -5,9	14
5,9 – 6,4	8
6,4 – 6,9	5
6,9 – 7,4	5
7,4 – 7,9	4
7,9 – 8,4	7

Задание 5

Охарактеризовать распределение субъектов РФ по показателю «Уровень безработицы», используя показатели:

• центра распределения (средняя арифметическая, медиана и мода);

• колеблемости признака (размах вариации; дисперсия; среднее линейное и квадратическое отклонения; коэффициент вариации; относительное линейное отклонение);

• формы распределения (показатель асимметрии и показатель эксцесса, а также их ошибки);

• структурные характеристики ряда распределения (квартили, квартильное отклонение и коэффициент квартильной вариации; децили и коэффициент децильной дифференциации; коэффициент фондовой дифференциации).

Показатели цента распределения.

1. Средняя арифметическая для ряда распределения с равными интервалами рассчитывается по формуле:

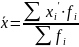
где середина интервала, частота интервала.

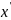
Уровень безработицы за 2012 г., в %	Количество регионов	Середина интервала	Накопленная частота S
4,9 – 5,4	7	5,15	7
5,4 -5,9	14	5,65	21
5,9 – 6,4	8	6,15	29
6,4 – 6,9	5	6,65	34
6,9 – 7,4	5	7,15	39
7,4 – 7,9	4	7,65	43
7,9 – 8,4	7	8,15	50

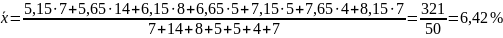
Вывод: в среднем в регионах уровень безработицы составляет 6,42 %.

2. Мода для ряда распределения с равными интервалами рассчитывается по формуле:

, где

нижняя граница модального интервала

величина интервала

частота модального интервала

частота интервала, предшествующая модальному

частота интервала, следующего за модальным

Мода находится в интервале с наибольшей частотой. В моем ряду распределения это второй интервал.

Вывод: чаще всего в регионах уровень безработицы за 2012 год составил 5,67 %.