Алгоритм разводки проводных соединений с заданными начальной и конечной вершинами
В некоторых случаях, помимо ограничения на степень вершин связывающего дерева, задается начальная и конечная точка цепи, например, источник и нагрузка. Задача сводится к построению кратчайшего пути между двумя заданными выводами, проходящего через все остальные точки. Эта задача родственна задаче коммивояжера, но путь обхода разомкнут. Таким образом, это задача построения гамильтоновой сети между начальной и конечной вершинами.
Рассмотрим приближенный алгоритм. Его суть отражается следующей последовательностью действий:
n-1 шаговый процесс выбора кратчайших ребер в полном графе;
проверка каждого ребра на выполнение ограничений задачи;
составление пути из выбранных ребер.
Алгоритм:
составляется упорядоченная по возрастанию длин последовательность ребер полного графа;
очередное ребро i=1,2,…,n-1 выбирается по порядку из этой последовательности при выполнении следующих условий:
ребро не соединяет конечную и начальную точки;
степень вершин, соединяемых ребром, не превышает допустимой (λ=1 – для начальной и конечной точек и λ=2 для остальных);
ребро не образует цикла с ребрами, уже включенными в путь;
при включении любого ребра в путь, кроме (n-1)-го , начальная и конечная точки не связываются.
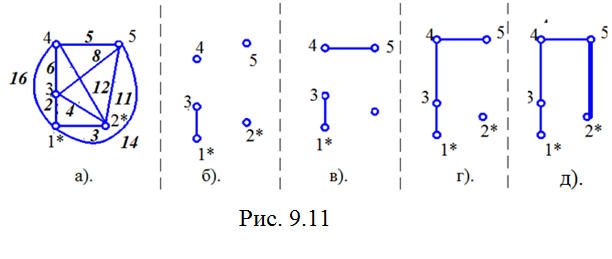
Рассмотрим пример. На рис. 9.13 (а) заданы клеммы выводов. Выводы 1* и 2* - конечные, степень вершины у них равна единице. У остальных – степени равны 2. Курсивом указаны длины ребер. Построить кратчайший путь между вершинами 1и 2.
составим упорядоченную по возрастанию длин последовательность ребер:
2
3
4
5
6
8
11
12
14
16
1*-3
1*-2*
2*-3
4-5
3-4
3-5
2*-5
2*- 4
1*-5
1*-4
выбираем ребро (1*-3), т.к. оно удовлетворяет всем условиям - рис. 9.13(б);
Ребро (1*-2*) не удовлетворяет условию 1; ребро (2*-3*) - условию 4, их не выбираем. Берем ребро (4–5) - рис. 9.13(в);
выбираем ребро (3–4) рис. 9.13(г). Ребро (3–5) отбрасывается, т.к. не выполняется условие 3.
Берем ребро (2*-5). Образовался путь 1*-3-4-5-2*. Длина пути равна 2+6+5+11=22. Задача решена.
Построение печатных соединений
Большинство алгоритмов основано на волновом алгоритме, который еще называют алгоритмом Ли.
Считаем, что монтажная схема – дерево, и хотя получение плоского изображения всегда возможно, при ограниченных размерах монтажной плоскости требуются специальные алгоритмы. Пусть задана монтажная плоскость с контактами, объединенными в подмножества (не пересекающиеся) по принадлежности к цепям. Пусть заданы запрещенные для прокладки области.
Требуется соединить контакты в каждом подмножестве, чтобы цепи не пересекались.
Разобьем плату на ячейки, например, квадраты, и будем считать их допустимыми или недопустимыми для прокладывания на данном шаге. На каждом шаге используются допустимые ячейки, число которых с каждым шагом убывает.
Допустим, на некотором шаге алгоритма необходимо соединить контакт S (исток) с контактом T (стоком). Т.е. речь пойдет о построении оптимального пути между двумя известными ячейками. Назначение истока и стока – произвольные. Считаем, что центр каждой ячейки соответствует контакту. Для каждого узла определим соседние узлы. В алгоритме Ли узлы, соседние к данному узлу – узлы, имеющие у своей ячейки общее ребро с заданным квадратом. Тогда линия связи может быть линией или ломаной с углом перегиба 900.
Для соединения истока и стока применяется метод расстановки пометок, который заключается в последовательном приписывании каждому узлу пометок, состоящих из двух частей: номера узла, из которого помечен данный, и номера итерации, на которой произошло присвоение пометки.
В алгоритме Ли этот процесс называется распространением волны, а пометки множества узлов, помеченных на каждой итерации – фронтом волны. Если в этом процессе произошел прорыв , т.е. получил пометку сток Т, то это значит, что может быть установлена связь между S и T, которая на этапе проведения пути осуществляется по меткам. В противном случае пути нет.
Сначала пометку
(-,
(S)=0)
получает исток S.
Эта пометка означает, что нет узла, из
которого помечается исток (-),
и итерация этой пометки нулевая
(
(S)=0),
затем помечаются все соседние к истоку
узлы. Например, узлы x,y,z,u
c
пометками
(S,ε(x)=1),
(S,ε(y)=1),
(S,ε(z)=1),
(S,ε(u)=1)
и т.д.
При этом, если некоторый узел может быть помечен из различных соседних узлов с разными пометками, то он помечается из узла с минимальным значением ε. Тогда вторая часть новой пометки должна быть равна ε+1.
Если несколько узлов имеют одинаковое минимальное ε, то берется любой из них, для пометки соседних.
Если пометился сток Т, то восстанавливается путь из Т в S, идя по пометкам (их левым частям). Правые части пометок позволяют оптимизировать выбор маршрута из истока в сток.
Таким образом, метод позволяет построить путь с минимальным числом шагов.
Пример
Соединить узлы S и T, сеть узлов N=(S,T,x1,x2,…,x10,x11).
Принцип работы алгоритма ясен из рисунка.
S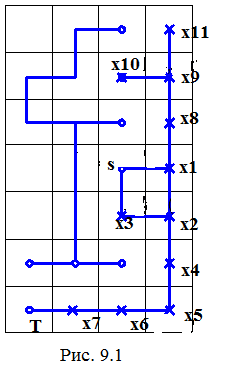
(-,ε(s)=0)
x1(s, ε(x1)=1)
x3(s, ε(x3)=1)
x2(x1, ε(x2)=2)
x4(x2, ε(x4)=3)
x5(x4, ε(x5)=4)
x6(x5, ε(x6)=5)
x7(x6, ε(x6)=6
Т(x7, ε(Т)=8)
x8(x1, ε(x8)=2)
x9(x8, ε(x9)=3)
x10(x9, ε(x10)=4)
x11(x9, ε(x11)=4)
конец, путь не найден, возвращаемся в вершину с вариантами x2 или x3.