Алгоритмы трассировки соединений

В алгоритмическом плане задача трассировки состоит в построении для всех цепей оптимальных монтажных соединений.

Постановка задачи заключается в следующем. Дана принципиальная электрическая схема, на которой определены цепи и связанные с ними контакты элементов. Дано размещение элементов на плоскости. Требуется построить монтажные соединения. Например (см. рис. 9.1):

а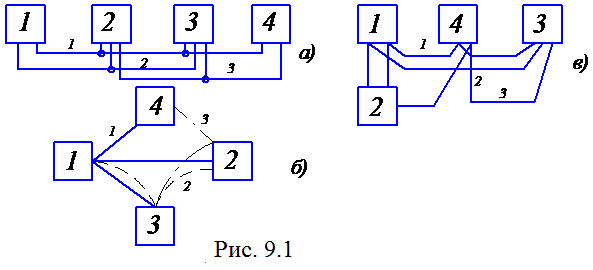 ) принципиальная электрическая схема;

б), в) схемы электрических соединений.

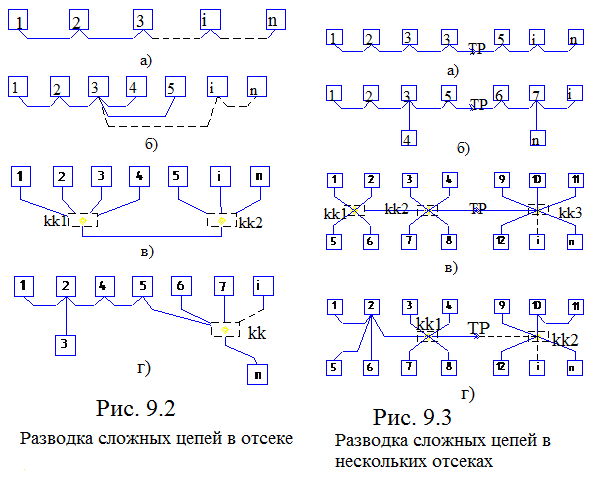
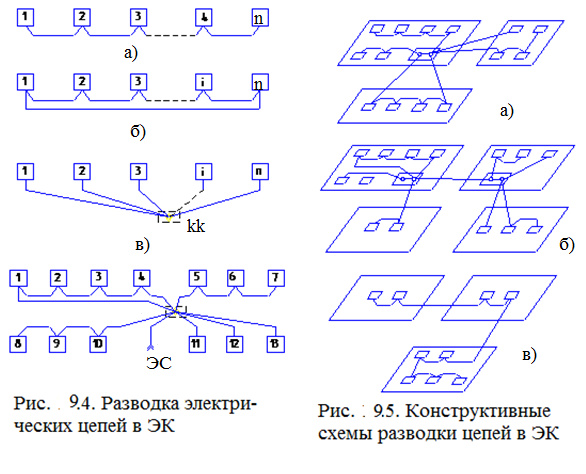
На рис. 9.2-9.5 даны примеры конфигурации разводки электрических цепей автономных объектов.

Алгоритмы трассировки проводных соединений

П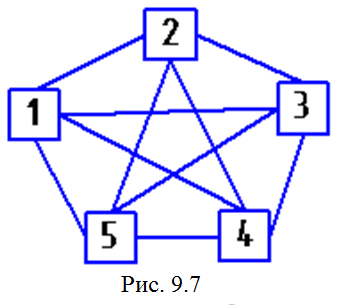 усть задана электрическая цепь (рис. 9.6) и соединенные ею элементы.

О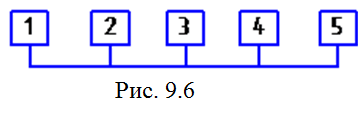 ни могут быть представлены полным графом (рис. 9.7).

Из этого графа надо выделить суграф заданной конфигурации, представляющий схему электрических соединений.

Р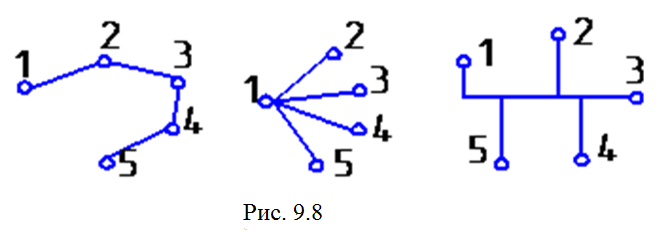 ассмотрим типовые конфигурации. Если не заданы жесткие требования надежности, то это может быть разомкнутая конфигурация, т.е. из графа надо выделить дерево. При этом могут быть заданы ограничения на степень вершин, а могут и не задаваться (рис. 9.8).

Для внутреннего монтажа коробок используются и замкнутые цепочки, и особенно сложная конфигурация имеет место при наличии клеммных колодок. Они неизбежны, если клеммы некоторых элементов допускают подключение только одного провода.

Алгоритм Прима

Пусть имеется множество точек плоскости P=p₁,p₂,…,p_n, соответствующих выводам произвольной цепи. Пусть эта цепь описывается полным графом G=(E,U), вершины которого соответствуют выводам цепи, а ребра электрическим связям. Ребра с приписанным к ним «весом» характеризуют соединения меду парами выводов. Значение «веса» может быть равно, например, расстоянию между соответствующими точками множества P. Требуется найти минимальное покрывающее дерево (т.е. дерево, включающее в себя все вершины из E и имеющее минимальный вес ребер).

Наиболее эффективным из известных алгоритмов является алгоритм Прима:

1. для произвольного вывода цепи найти ближайший вывод и провести соединение;

2. на последующем шаге i = 2,3,…,n-1 из множества неподсоединненых выводов выбрать тот, который находится ближе остальных к группе yже связанных выводов и подсоединить его к этой группе по кратчайшему пути.

Построенное таким образом дерево будет иметь минимальную суммарную длину соединений.

При разработке монтажных соединений часто вводится ограничение на максимальное число соединений λ к клемме элемента, т.е. на степень вершины. Если λ<6 (до λ=6 алгоритм точный), то можно использовать модифицированный алгоритм Прима:

1. всякая изолированная вершина соединяется с ближайшей, не соединенной с λ другими вершинами;

2. всякий изолированный фрагмент соединяется кратчайшим ребром с ближайшей вершиной, не соединенной с λ другими вершинами.

Пример

Н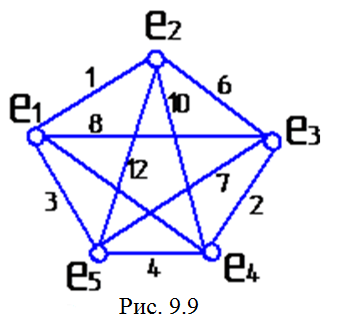 айти минимальное покрывающее дерево для графа, приведенного на рис. 9.9

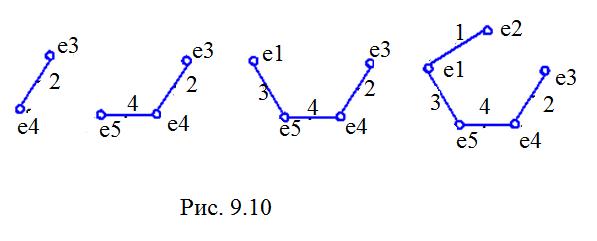
Н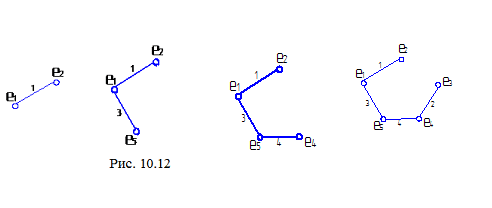 ачнем с вершины 1, ближайшая к ней вершина 2:

Ближайшая вершина к фрагменту вершина 5.

К этому фрагменту ближайшая вершина 4

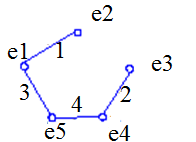
Ближайшая к этому фрагменту вершина 3.

Общая длина равна 10.

Решение не зависит, с какой вершины начинается построение. Самостоятельно провести построение, начав с вершины 4.

Например, начнем с вершины 4: