2. Расчет ускорений

При кинематическом анализе механизма считаем, что кривошип вращается с постоянной угловой скоростью, тогда ускорение а_А точка А вычисляется по формуле [1-3]:

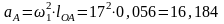м/с².

Ускорение а_B точки В шатуна связано с ускорением в точки А зависимостью:

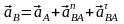, (2) где - переносное ускорение; 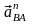и 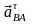- нормальная и тангенциальная составляющие относительного ускорения точки В.

Ускорение направлено параллельно кривошипу, из точки А к центру О вращения звена. Ускорение направлено параллельно шатуну, из точки В в точку А, а - перпендикулярно АВ.

Величина нормальной составляющей относительного ускорения в соответствии с [1-3] вычисляется по формуле

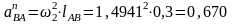м/с².

Ускорение 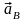направлено параллельно направляющей t - t ползуна.

Уравнение (2) имеет два неизвестных, графическое его решение приведено на рис. 5.

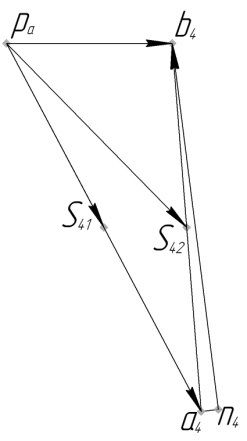
Рис. 5. План ускорений

Масштабный коэффициент плана ускорений:

.

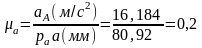
Длина отрезка, которым на плане ускорений изображается ускорение

.

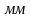Ускорение а_S1 и a_S2 центров масс звеньев определяются по свойству подобия плана ускорений.

Из этой пропорции следует .

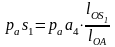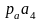Отрезок откладываем на плане ускорений (рис. 5) от полюса на прямой , получаем точку s₁. Отрезок изображает в масштабе 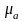ускорение центра масс кривошипа.

Для определения ускорения 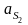центра масс шатуна составим пропорцию

Отрезок откладываем на плане ускорений (рис. 5) от точки а₄ на прямой , получаем точку s₂. Соединим ее с полюсом плана ускорений. Отрезок 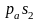изображает ускорение точки s₂.

Расчет ускорений:

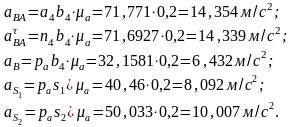
Угловое ускорение шатуна

Расчет ускорений выполнен для 2 положений механизма, результаты представлены в табл. 2.

Таблица 2

Ускорение № п/п	аА	aS1			aB	aS2
	м/с2							1/с2
4	16,184	8,092	0,670	14,339	6,432	10,007	47,797
5			2,181	8,459	15,405	37,959	28,197

2.2. Кинематический анализ методом кинематических диаграмм

Кинематические диаграммы позволят получить представление об изменении перемещения, скорости и ускорения ползуна за цикл, и определить их величины в любом положении механизма.

Диаграмма перемещения (рис. 6, а) строится в зависимости от времени. При ω₁=const каждому моменту времени соответствуют определенный угол φ₁ поворота кривошипа и соответствующее ему положение кривошипа. В связи с этим, по оси абсцисс откладываем не только время t, но и угол φ₁.

На оси абсцисс (рис. 6, а) откладываем отрезок длиной L = 180 мм. Он изображает в масштабе μ_φ угол поворота кривошипа за один его оборот.

.

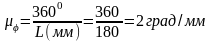Если угол поворота кривошипа измеряется в радианах, то

.

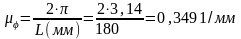Отрезок L изображает время цикла t_ц .

.

.

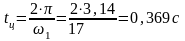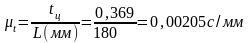Масштабный коэффициент μ_S оси ординат принят равным μ_l .

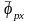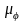Для построения диаграммы перемещения (рис. 6, а) определим длину отрезка , который в масштабе изображает угол рабочего хода.

.

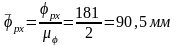Отложим на оси абсцисс от начала координат диаграммы перемещения отрезок , разделим его на шесть равных частей и обозначим концы отрезков соответствующих положениям механизма 1; 2; 3; 4; 5; 6. Отрезок 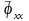тоже делим на шесть равных частей. Получим положения 7; 8; 9; 10; 11; 12. Из точек 1, 2, 3, . . . 11 на оси абсцисс проводим к ней перпендикуляры, на которых откладываем отрезки В₀В₁, В₀В₂, В₀В₃, и тд., изображающие перемещение ползуна в соответствующих положениях на разметке. Концы ординат соединяем плавной кривой.

Оси абсцисс диаграмм скоростей и ускорений совпадают с осью абсцисс диаграммы перемещений.

Для построения диаграммы скоростей (рис. 6, б) используем данные, приведенные в таблице 1. Примем масштабный коэффициент , оси ординат диаграммы V = V(t) равным μ_υ плана скоростей. Тогда отрезок, изображающий скорость ползуна на диаграмме в i - м положении механизма, равен 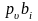при i = = 0, 1, 2, 3, . . . 12.

Для построения диаграммы ускорений (рис. 6, в) использован метод графического дифференцирования диаграммы скоростей [1].

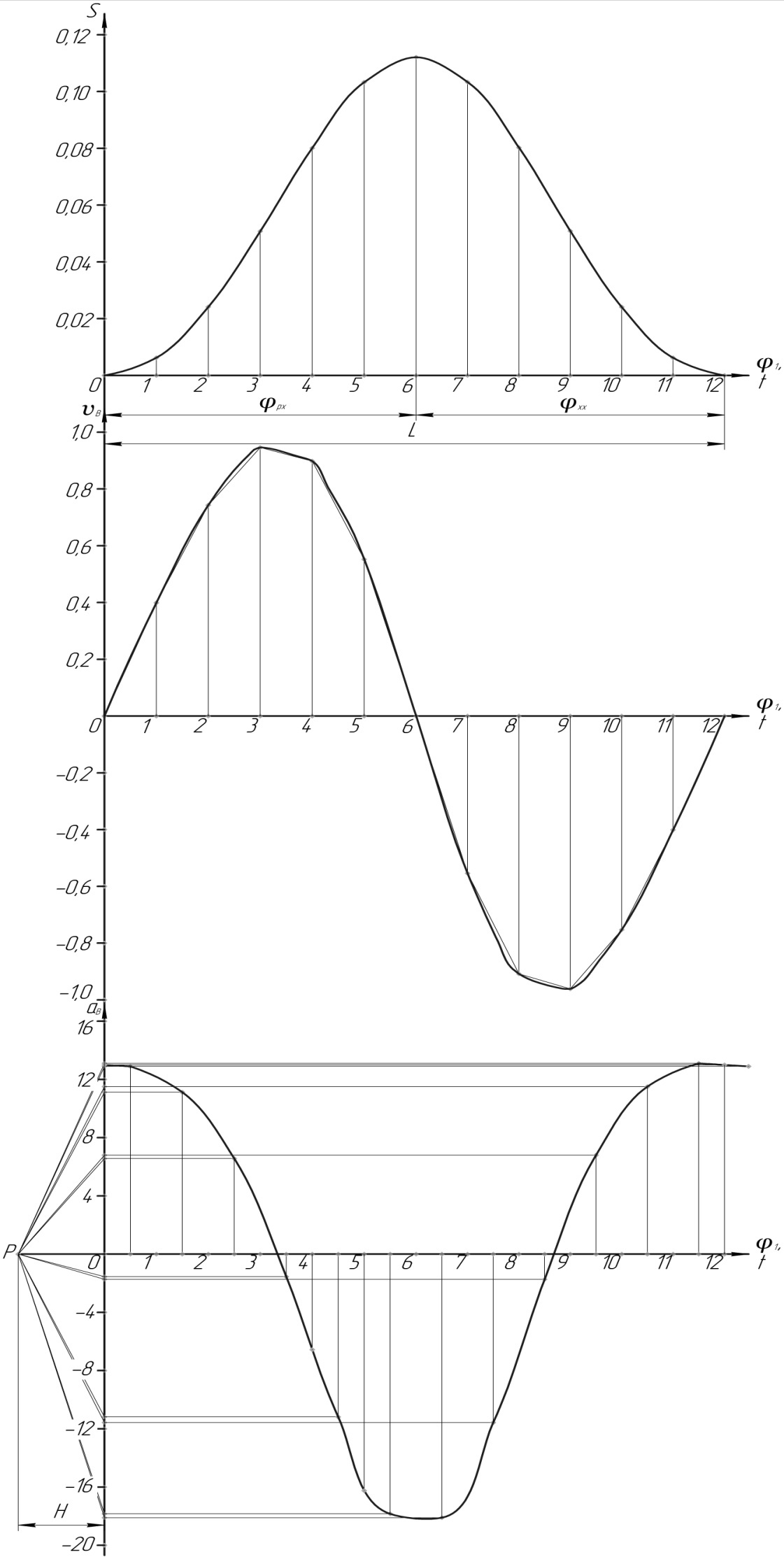
а)

б)

в)

Рис. 6. Кинематические диаграммы

Проводим хорду (рис. 6, б), которая соединяет концы начальной и конечной ординат кривой V(t) на рассматриваемом временном интервале. На оси абсцисс диаграммы ускорений (рис. 6, в) выбираем точку Р, находящуюся от начала координат на расстоянии H = 25 мм. Из этой точки проводим луч, параллельный хорде, до пересечения с осью а_В . Получаем отрезок, который в масштаб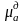е изображает среднюю величину ускорения на рассматриваемом временном интервале.

Подобным образом определяем среднее ускорение на всех временных интервалах. В результате получим ряд точек, каждая из которых расположена в середине временного интервала. Соединяем эти точки плавной кривой.

.

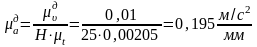Расчет величины ускорения ползуна графическим методом в рассматриваемых положениях механизма:

1). Положение 4

;

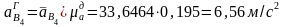2). Положение 5

.

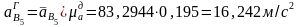Расхождение результатов, полученных методом планов и методом диаграмм, составляет 2 % и 5,4 % в положениях 4 и 5 соответственно.