Примеры:

1) Разложить по формуле бинома Ньютона: 1. ; 2. .

Решение:

1.

2.

.

2) Найти 6-й член разложения (5х² – 6а²)¹⁰.

Решение:

3) Вычислить

Решение:

.

4) В разложении вычислить член, не содержащий “x”.

Решение: .

.

, .

T₅ – не содержит “x”,

.

IV. Теория графов Основные понятия

Изучаемые явления, процессы, системы иногда удобно представить графически. Графические представления - удобный способ иллюстрации содержания различных понятий. Например, диаграмма Эйлера–Винна, гистограмма, круговые диаграммы и т.д. С помощью графиков можно судить о количественных соотношениях сравниваемых объектов, что значительно упрощает их анализ. С помощью графов решают многие задачи управления, сетевого планирования, принятия решений в условиях неопределенностей. При этом не все детали рисунка одинаково важны, например, длина, кривизна ребер, взаимное расположение вершин на плоскости. Графическое представление – это описание исследуемой системы с помощью вершин и ребер (дуг), соединяющих эти вершины.

Определение. Графом G называется совокупность двух множеств: вершин V и ребер E, между элементами которых определено отношение инцидентности – каждое ребро еЕ инцидентно ровно двум вершинам , , которые оно соединяет.

При этом вершина и ребро е называются инцидентными друг другу, а вершины и , являющиеся для ребра её концевыми точками, называются смежными. Часто вместо и еЕ пишут соответственно , еG. Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой. Тогда ребро называется направленным (ориентированным) или дугой и изображается стрелкой, направленной от вершины, называемой началом, к вершине, называемой концом. Граф, содержащий направленные ребра (дуги) с началом и концом , называется ориентированным (ор-графом) и ненаправленные - неориентированным (н-графом). Ребра, инцидентные одной и той же паре вершин, называются параллельными (кратными). Граф, содержащий кратные ребра, называется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей. Если множество его элементов графа (вершин и ребер) конечно, то он называется конечным. Если же множество вершин V (ребер Е) пусто, то граф называется пустым. Граф без петель и кратных ребер называется полным, если каждая пара вершин соединена ребром.

Дополнением графа называется граф , имеющий те же вершины, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, что бы получить полный граф. Каждому неориентированному графу канонически соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инцидентными тем же вершинам и имеющими противоположные направления.

Локальной степенью (или просто степенью) вершины н – графа G называется количество ребер , инцидентных вершине . В н-графе сумма степеней всех вершин равна удвоенному числу ребер “m” графа, т.е. четна (в графе с петлями петля дает вклад 2 в степень вершины).

В н-графе число вершин нечетной степени четно. Для вершин графа определяются две локальные степени:

1. - число ребер с началом в вершине (количество выходящих из ребер);

2. - количество входящих в вершину ребер, для которых эта вершина является концом.

Петля дает вклад 1 в обе эти степени. В орграфе суммы степеней всех вершин и равны количеству ребер этого графа и равны между собой:

.

Графы G₁ и G₂ равны G₁=G₂, если их множества вершин и ребер (выраженных через пары инцидентных им вершин) совпадают: V₁=V₂ и Е₁=Е₂. Граф G считается полностью заданным, если нумерация его вершин и ребер зафиксирована. Графы, отличающиеся только нумерацией вершин и ребер, называются изоморфными.

Пример 1:

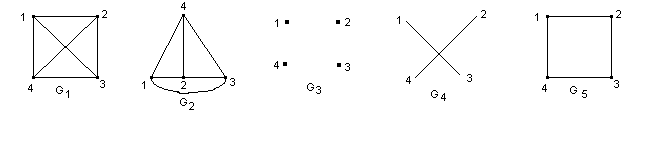
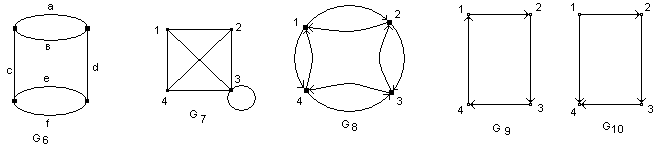
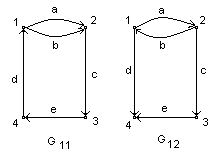Рис 1.

G₁ – G₇ – неориентированные графы;

G₈ – G₁₂ – орграфы, G₁ = G₂ ;

G₇ – не является полным, хотя каждая пара вершин соединена ребром, но имеется одна петля;

G₃ – все вершины этого графа являются изолированными, т.е. Е = 0;

G₄ – G₅ – являются дополнением друг другу ;

G₆ – мультиграф, т.к. содержит кратные ребра а и в, е и f;

G₈ – ориентированный граф, канонически соответствующий Н – графу G₅;

G₉ – G₁₀ – не равны, т.к. имеют отличающиеся ребра;

G₁₁ – ор.граф (мультиграф), а и в – кратные;

G₁₂ – не мультиграф (а и в различно ориентированы).

Пример 2:

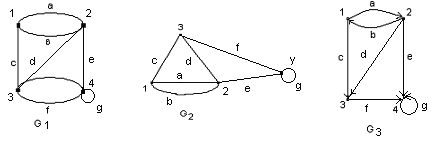
Рис.2

G₁ и G₃ – оба графа имеют по четыре вершины V = {1, 2, 3 ,4}.

Степени вершины н – графа :  (1) =3,  (2) =4,  (3) =3,  (4) =4.

Тогда , т.е. равна , где 7 – число ребер графа.

Степени вершин орграфа :

₁ (1) =2, ₁ (2) =3, ₁ (3) =1, ₁ (4) =1, ₂ (1) =1, ₂ (2) =1, ₂ (3) =2, ₂ (4) =3.

Тогда (число ребер).