Контрольная работа №5

1. Определить результаты действий АВ, АВ, А\В, В\A, А+В:

1.

2.

2. Найти (АВ)С и (АВ)\С, если

3. Оценить множество

4. Оценить множество С=АВ, если

5. Найти декартовые произведения , если

6. Определить область определения и область значений для функции . Построить график функции.

7. Определить обратную функцию , если и построить на одном чертеже графики функций и .

8. Сложную функцию представить в виде цепочки из простых функций.

9. Если , а то определить сложные функции .

Контрольная работа №6

1. Определить истинность или ложность высказываний:

_,

,

_;

решить задачи 1, 2.

1. Определить истинность или ложность предложений

xy, yz, yx, xz, x , .

2. Определить логическое значение формул

а) ((ху)z)((хz)(yz));

в) (ху)(хz) (xyz).

2. Для произвольных высказываний ( ) построить таблицу истинности для формул:

1)  ; 2) .

3. Даны предикаты Р(х): “х – нечетное число” и Q(х): “х – делится на 10”. Найти область истинности предикатов Р(х)Q(х) и Р(х)Q(х), если исходные предикаты определены на множестве N.

4. Вычислить:

а) ;

в) .

5. В учебной группе студентов. Сколькими способами их можно разбить на бригады по Р₁ человек?

6. В оперативной группе имеется Р₁+Р₂+Р₃ солдат и 4 офицера. Сколькими способами можно назначить наряд, состоящий из 3 солдат и 1 офицера?

7. Сколькими способами можно составить (Р₁+Р₂) – значное число, в состав

которого входят две двойки и три шестерки?

8. На иномарке, скрывшейся с места ДТП, был Р₁ – значный номер, в котором имелось три четверки, а остальные цифры не повторялись. Сколько номеров необходимо проверить по картотеке ГИБДД, чтобы найти нарушителя?

9. Сколькими способами можно составить шеренгу из Р₁ рядовых, Р₂ лейтенантов и Р₃ прапорщиков?

10. Составим слово из имени и фамилии студента. Сколькими способами можно переставить буквы в этом слове, что бы получились все возможные различные наборы букв?

11. В расположении командующего армией имеется Р₂ родов войск. Сколькими способами можно составить Р₃ соединений для проведения войсковой операции?

12. Сколькими способами можно упаковать (Р₁+Р₂+Р₃) различных книг в три ящика соответственно по Р₁, Р₂, Р₃ книги в каждом ящике?

13. Составить матрицы инцидентности, смежности и список ребер для графов:

1)

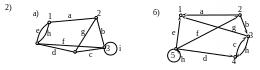
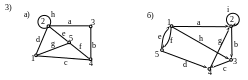
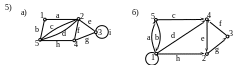
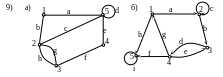
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ЗА ВТОРОЙ СЕМЕСТР

(Дискретная математика)

1. Множество. Конечные и бесконечные множества.

2. Сумма (объединение) и произведение (пересечение) множеств. Свойства.

3. Разность двух множеств. Сумма разностей множеств.

4. Бинарное (декартовое) произведение двух множеств.

5. Табличное и стрелочное представления бинарного отношения.

6. Взаимно - однозначное соответствие между множествами.

7. Понятие мощности множества.

8. Счётные и несчётные множества. Мощность счётного и несчётного множества.

9. Нижняя и верхняя грани множества.

10. Диаграмма Эйлера – Венна.

11. Алгебра высказываний.

12. Операция отрицания.

13. Сумма (дизъюнкция) высказываний. Таблица истинности. Свойства.

14. Произведение (конъюнкция) высказываний. Таблица истинности. Свойства.

15. Импликация высказываний. Таблица истинности. Свойства.

16. Эквивалентность высказываний. Таблица истинности. Свойства.

17. Равносильность формул. Свойства равносильности.

18. Предикаты.

19. Кванторы существования и общности.

20. Размещения без повторений. Число размещений.

21. Перестановки без повторений. Число перестановок.

22. Сочетания без повторений. Число сочетаний.

23. Принцип умножения.

24. Принцип сложения.

25. Перестановки с повторениями. Число перестановок.

26. Размещения с повторениями. Число размещений.

27. Сочетания с повторениями. Число сочетаний.

28. Бином Ньютона. Свойства.

29. Определение графа. Виды. Свойства.

30. Способы задания графов.

31. Построение матрицы инцидентности, матрицы смежности и списка ребер.

Литература

Теория множеств:

1. Александров П.С. Введение в общую теорию множеств, огл 3, гостех издат, 1948.

2. Фор Р., Кофман А., Дени-Папен М., Современная математика, Мир, М, 1966.

3. Портер У. Современные основания общей теории систем.

4. Мышкис А.Д. Лекции по высшей математике.

5. Нефедов В.Н., Осипова В.А., Курс дискретной математики, 1992.

Элементы математической логики:

1. Эдельман С. Л. Математическая логика. М.: Высшая школа, 1975.

2. Колмогоров А. Н., Драгалин А. Г. Введение в математическую логику. М.: Изд- во МГУ, 1982.

3. Нефедов В.Н., Осипова В. А. Курс дискретной математики. М.: Изд-во МАИ, 1992.

4. Новиков П. С. Элементы математической логики. М.: Наука, 1973.

Элементы комбинаторики. Бином Ньютона.

1. Ф. Мостеллер, Р. Рурке, Дж. Томас. Вероятность. Изд- во Мир, М.: 1969.

2. А.П.Киселев. Алгебра, II ч.: 1957.

Теория графов:

1. Москинова Г.И. Дискретная математика. М.: Логос. 2002.

2. О. Оре. Графы и их применение. М.: Мир. 1965.

3. К. Берж. Теория графов и ее применение. М.: Ин. литер. 1962.

4. Новиков Ф.А. Дискретная математика (для программистов). М.: Питер. 2000.

61