2.6.1. Волны e-типа в планарном диэлектрическом волноводе на металлической подложке.

Исключив составляющие и из системы уравнений (2.6), для H-волн, приходим к последующим скалярным уравнениям для в каждой из сред (рис. 2.7):

, при

где

, при x>t, (2.34)

где

Общее решение уравнений (2.34) с учетом условия убывания поля при по аналогии с (2.18) имеет вид:

(2.35)

Для определения постоянных , B, С, h, p воспользуемся граничными условиями аналогичными (2.9). Тогда, учитывая, что первая среда (подложка) является идеальным проводником:

. (2.36)

При этом в соответствии с (2.6)

, , где . (2.37)

Подставляя (2.37) в граничное условие и учитывая (2.35), получаем , т.е. В=С.

Тогда общее решение (2.35) волнового уравнения принимает вид

(2.38)

где – некий новый коэффициент.

Из двух оставшихся граничных условий в (2.36) получаем

(2.39)

Система (2.39) для определения отличных от нуля коэффициентов совместна, если

. (2.40)

Раскрывая соотношение (2.40), получаем характеристическим уравнением для E– мод в планарном диэлектрическом волноводе на металлической подложке

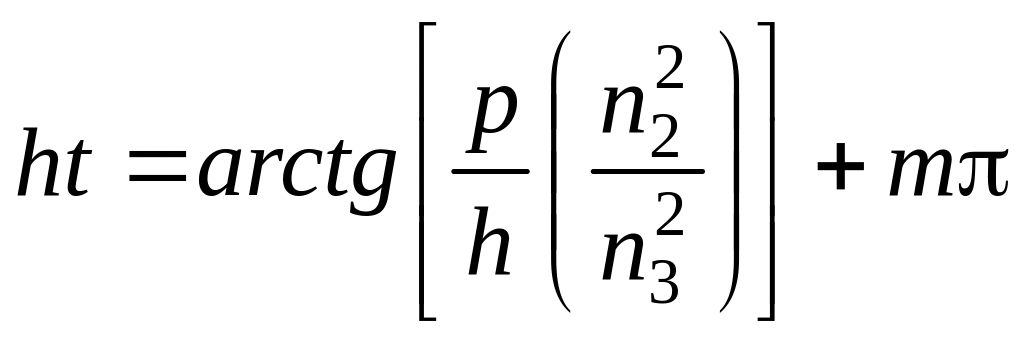, где m=0,1,2,3… – индекс моды. (2.41)

Задание: объяснить (2.40) и получить (2.41) .

Кроме того в соответствии с (2.34)

. (2.42)

Выражая через из (2.39), учитывая с (2.38) и (2.37), получаем следующее представление для компонент электромагнитного поля:

, , где . (2.43)

Из (2.43) следует, что в рассматриваемой структуре могут существовать только четные Е-волны и т.д. (индекс моды m = 0, 2, 4…), поскольку в соответствии с (2.36) электрическое поле в диэлектрической пленке на металлической подложке должно удовлетворять граничным условиям на поверхности металла.

Задание: пояснить последнее утверждение.

Задание: Используя (2.41), (2.42) записать условие, аналогичное (2.33), позволяющее найти число распространяющихся Е-мод в планарном диэлектрическом волноводе на металлической подложке, зная параметры .

2.6.2. Волны H-типа в планарном диэлектрическом волноводе на металлической подложке.

По аналогии с 2.6.1 будем исследовать H -моды в диэлектрическом планарном волноводе на металлической подложке. Единственными ненулевыми составляющими поля в этом случае в соответствии с (2.5) будут . Снова решение ищется в виде (сравни с (2.35)):

(2.44)

Характеристическое уравнение и соотношение между постоянными h, p выводятся так же, как и для E-мод:

, где m=0,1,2,3… – индекс моды,

. (2.45)

Соответствующие компоненты электромагнитного поля для H-мод имеют вид:

(2.46)

Задание: провести по аналогии с разделом 2.6.1. все рассуждения для H-волн.

Из (2.46) следует, что в рассматриваемой структуре могут существовать только нечетные H-волны и т.д. (индекс моды m = 1, 3, 5…), поскольку в соответствии с (2.36) электрическое поле в диэлектрической пленке на металлической подложке должно удовлетворять граничным условиям на поверхности металла.

Задание: Используя (2.45) записать условие, аналогичное (2.33), позволяющее найти число распространяющихся H-мод в планарном диэлектрическом волноводе на металлической подложке, зная параметры .