2.5. Моды в симметричном планарном диэлектрическом волноводе

В симметричном волноводе (см. рис. 2.1,в) n₁=n₃. Из первых двух уравнений в (2.16), (2.19) следует, что при n₁=n₃ имеем p=q. Подставив p=q и n₁=n₃ в последнее уравнений (2.16) и (2.19) и сделав для удобства замену t=2d, получим:

для Н-мод (2.29)

для Е- мод

Тогда характеристические уравнения для симметричного волновода толщиной t=2d будут иметь вид

для Н- и Е-мод

(2.30а)

Н-моды, (2.30б)

Е-моды. (2.30в)

Как и в случае асимметричного планарного диэлектрического волновода, систему трансцендентных уравнений (2.30,а), (2.30,б) или (2.30,а), (2.30,в) можно решить графически (рис. 2.6,а), причем в случае симметричного волновода решение допускают все значения m_c=0,1,2,3..., как четные, так и нечетные (рис.2.6,б).

Для нахождения распределения поля в симметричном волноводе, удобнее сдвинуть систему координат к средней плоскости пленочного волновода (рис.2.1,в): . Тогда с учетом сказанного выше для области [сравни с (2.17), (2.20)]

Н-моды (2.31а)

Е-моды (2.31б)

Выражение (2.31) поясняет смысл четности и нечетности мод в симметричном планарном волноводе относительно координаты x , приведенной на рисунке 2.1,в.

Рис 2.6. К графическому решению системы уравнений в случае симметричного волновода

Задание: записать все компоненты четных и нечетных Н- и Е-мод, используя (2.17), (2.20).

Дисперсионные уравнения для четных и нечетных мод в симметричном пленочном волноводе можно вывести из (2.26), (2.47), учитывая особенности симметричного волновода (n₁=n₃, k₁=k₃),

- четные Н-моды; (2.32а)

- нечетные Н- моды; (2.32б)

- четные Е-моды; (2.32в)

- нечетные Е- моды, (2.32г)

где все обозначения аналогичны обозначениям в (2.26), (2.27).

На примере симметричных пленочных волноводов отметим еще раз особенности рассматриваемых диэлектрических и металлических волноводов.

Во-первых, новая волна, появляющаяся в диэлектрическом волноводе, на критической частоте (см. рис. 2.4,а; 2.6,б) имеет волновое число p=q=0 и в соответствии с (1.25) . Таким образом, волна распространяется со скоростью равной фазовой скорости плоской волны в безграничной среде с параметрами, совпадающими с параметрами среды, окружающей диэлектрический волновод. В то время как в металлическом волноводе при критической частоте =0.

Во-вторых, при частоте ниже критической в диэлектрическом волноводе моды данного типа вообще не существуют, а в металлическом волноводе она существует в виде затухающей волны.

По аналогии с (2.24) (используя рисунок 2.26) можно записать условие, позволяющее найти число распространяющихся Н- и Е-мод в симметричном диэлектрическом пленочном волноводе, зная параметры :

где m_c=0,1,2… (2.33)

2.6. Волны в планарном диэлектрическом волноводе на металлической подложке

Данная линия передачи показана на рис 2.7. Волновод попрежнему является бесконечно протяженным в направлении оси OY и изменения поля в этом направлении нет, то есть .

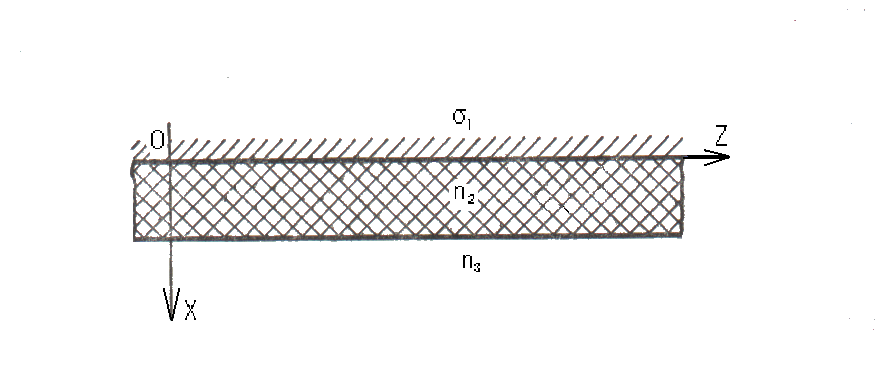
Рис 2.7. Планарный диэлектрический волновод на металлической подложке.

Для определения структуры электромагнитного поля и основных характеристик полагаем металлическую подложку идеально проводящей, используем уравнения электродинамики (2.2), (2.3), представление бегущих волн вдоль оси z (2.4) в виде E- и H-волн (2.5), (2.6) соответственно.