2.3. Волны e–типа в асимметричном планарном диэлектрическом волноводе

По аналогии с разд. 2.1, 2.2 , выполняя все задания, будем исследовать E-моды в диэлектрическом планарном волноводе. Единственными ненулевыми составляющими поля в этом случае будут ; граничные условия отличаются от (2.9).

Решение ищется в виде [сравни с (2.10)]:

(2.18)

Характеристическое уравнение и соотношение между постоянными h, q, p выводятся так же, как и для H-мод, однако следует иметь в виду, что диэлектрические проницаемости слоёв различные. В результате получим систему уравнений, определяющих постоянными h, q, p для E -мод:

. (2.19)

Эти уравнения отличаются от уравнения (2.16) для H–мод только наличием квадрата отношений показателей преломления в аргументах арктангенса; E–моды обозначаются как и т.д.

Составляющие поля для E -мод записываются с учетом (2.6) следующим образом:

(2.20)

, .

2.4. Классификация мод в планарном диэлектрическом волновод

В асимметричном планарном волноводе (рис. 2.1,а,б) для показателей преломления , как правило, выполняются условия: . Поэтому соотношения

(2.21)

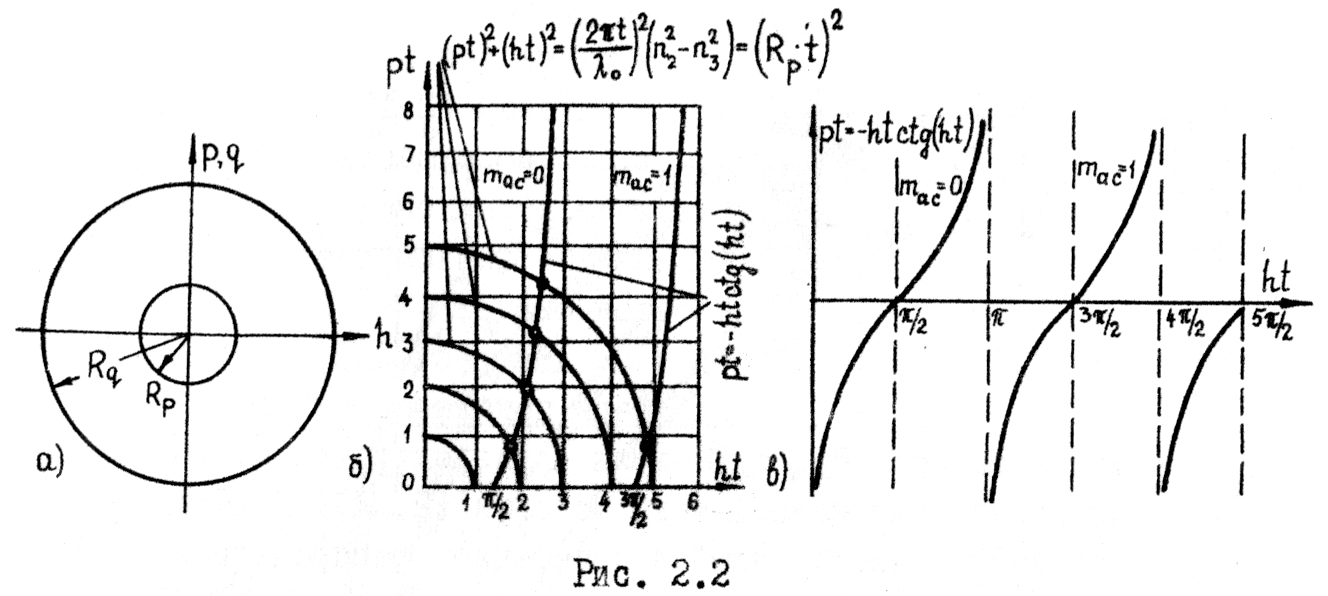
представляют собой в системе координат (q, h), (p, h) уравнения окружностей с сильно различающимися радиусами R_q и R_p (рис. 2.2,а). Отсюда q>>p и q>>h при любых h. Кроме того, и .

Теперь рассмотрим зависимость : при угол . Поскольку и , последние уравнения в (2.16), (2.19) можно привести к следующему виду:

для H-мод ; (2.22)

для E-мод .

Так как , система уравнений для H – и E -мод асимметричного волновода с учетом (2.21), (2.22) примет вид

;

;

. (2.23)

В рассматриваемом приближении H– и E-моды сильно асимметричном волноводе вырождены, т.е. поперечные волновые числа h, q, p для m-й моды одинаковы в случае H - и E -мод.

Поперечное волновое число q однозначно находится из первого выражения в (2.23). Систему двух последних трансцендентных уравнений (2.23) относительно h и p можно решить (при желании получить большую точность) одним из численных методов (см. разд. 3), либо более наглядным и простым графическим методом (однако, он обладает сравнительно невысокой точностью).

Решения двух последних уравнений (2.23) представлены на рис. 2.2,б графически на плоскости pt–ht. Совместное решение этих уравнений есть точки пересечения двух кривых, соответствующие модам пленочного волновода. Поскольку величина p должна быть положительной [см. (2.10),(2.18)], следует ограничиться только первым квадрантом (рис. 2.2,в поясняет это). Как следует из рис.(2.2,б), при распространяющихся волноводных мод не существует. Только когда частота колебаний (или разность показателей преломления) становится настолько большой, что , круг радиуса впервые пересекает ветвь m=0 кривой. Это – решение системы из двух последних уравнений (2.23) для m=0; оно описывает в рассматриваемом приближении и - волны, которые являются основными волнами плоского несимметричного диэлектрического волновода. Из выражения для видно, что число волноводных мод зависит от параметров, которые можно изменять, а именно . Так, при в волноводе, кроме – и -мод, распространяются еще две моды и и т.д. Радиус окружности (следовательно, и значение ) для m-й моды должен лежать в пределах

(2.24)

где

Соотношение (2.24) позволяет, зная параметры , найти число распространяющихся мод в волноводе или, наоборот, подобрать эти параметры, исходя из требований.

Найденные значения pt и ht позволяют определить с учетом (2.15) постоянную распространения Г, фазовую скорость и длину волны в линии , а также все компоненты поля из выражений (2.17) или (2.20), т.е., по существу, решить задачу о нахождении мод в планарном асимметричном диэлектрическом волноводе.

На рис.2.3 в качестве примера показано распределение компоненты поля –волн в диэлектрическом волноводе в случае выполнения для каждой моды условия (2.24). Порядок m волны равен, как видно, числу нулей в поперечном распределении поля.

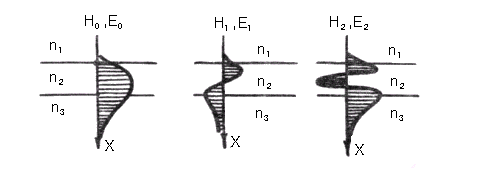
Рис 2.3. Распределение компоненты поля

Удобно для исследования дисперсионных характеристик ДВ (зависимости продольного волнового числа Г от частоты ) записать характеристические уравнения (2.16), (2.19) в виде, непосредственно связывающем Г с параметрами сред и с частотой. Из (2.15) следует, что

(2.25)

где , с- скорость света.

Подставляя (2.25) в (2.16) и (2.19), получаем для симметричного волновода в случае Н-мод

(2.26)

и, соответственно, в случае Е-мод

. (2.27)

Соотношения (2.26), (2.27) представляют собой дисперсионные уравнения и при заданных позволяют проследить зависимость Г от для каждой Н- и Е-моды порядка m. Пример численного решения этих уравнений дан на рис.(2.4,а,б), где – относительная толщина пленки, – эффективный показатель преломления.

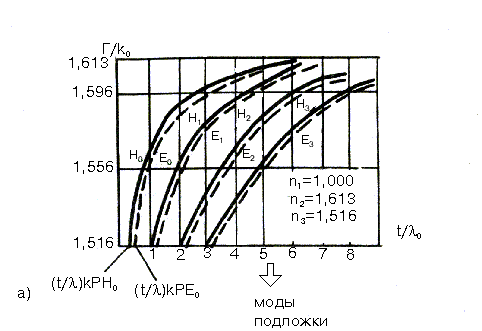
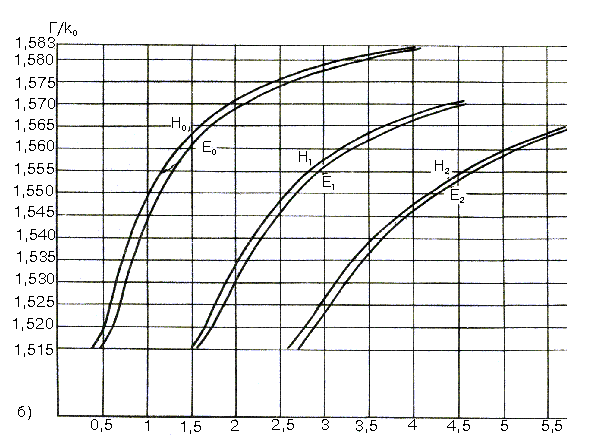
Рис.2.4. Дисперсионные кривые.

Численные методы решения дисперсионных уравнений с их программной реализацией рассмотрены в разделе 3. Несовпадение кривых для Н- и Е-мод с одинаковым индексом m вызвано тем, что уравнения (2.21), исследованные ранее (см. кривые на рис.2.2), были получены при упрощающих предположениях. Однако в изотропных диэлектрических волноводах это различие невелико и практически трудно получить одномодовый режим (единственная волна Н₀).

Поскольку в случае направляемых поверхностных мод постоянные h,q,p – положительные действительные величины, то из (2.25) следует, что

где При в соответствии с (2.17), (2.20) волна представляет собой экспоненциальную функцию во всех трех областях (рис. 2.5,а), так что поле неограниченно возрастает вне диэлектрического волновода.

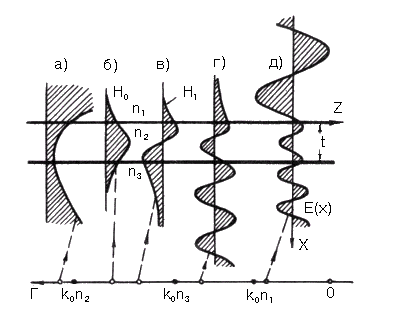
Рис. 2.5. Структура поля для различных режимов

Такое решение физически бессмысленно и практически нереализуемо. Соответственно на графике, приведенном на рис. 2.4,а, .

При из (2.17), (2.20) следует, что волна представляет собой гармоническую функцию в области n₂ и убывает по экспоненциальному закону в областях n₃ (подложки) и n₁ (покрытия) (см. рис.2.1). Поскольку энергия, переносимая такими типами волн, сосредоточена вблизи волноводного слоя n₂ , эти волны называются поверхностными (волноводными). Два таких решения показаны на рис.2.5,б,в.

При поле (2.17), (2.20) имеет экспоненциально убывающий характер в области n₁ и гармонический в областях n₁, n₃.Такие волны не удовлетворяют физическому условию убывания при x и соответствуют так называемым излучательным модам подложки (рис. 2.5,г). Тогда на графике, приведенном на рисунке 2.4,а нижняя граница отношения .

Наконец, при структура волны становится гармонической во всех трех областях (рис.2.5,д), что соответствует излучательным модам волновода.

Физический смысл ограничений (2.28) состоит в том, что фазовая скорость мод должна быть не больше плоских волн, распространяющихся в материале подложки с показателем преломления n₃, и не меньше плоских волн в волноводном слое с показателем преломления n₂.