2.1. Исходные соотношения строгой электродинамической теории
Пленочные диэлектрические волноводы имеют некоторые общие черты с полыми металлическими волноводами. В частности, и те и другие могут поддерживать ограниченное число направленных типов волн-мод на любой заданной частоте; в обеих структурах возможно преобразование мод, если форма волновода отклоняется от идеальной прямолинейной и т.п. В тоже время имеется и существенные различия, вызванные в первую очередь тем, что электромагнитное поле поле существует строго внутри металлических волноводов, а в ДВ оно формально существует во всём пространстве.
Исследуем
направляемые (волноводные) моды на
примере планарного регулярного
диэлектрического волновода (рис 2.1,
а-б). Для простоты далее будем полагать,
что волновод является бесконечно
протяженным в направлении оси OY
и изменения поля в этом направлении
нет, то есть
.
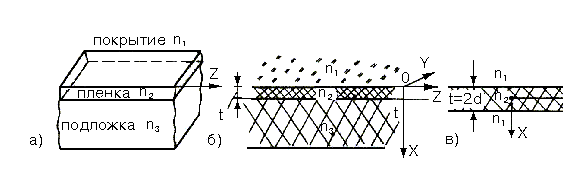
Рис 2.1.Планарный диэлектрический волновод
Ограничимся
случаем монохроматического поля с
временной зависимостью
,
где
–круговая частота. Для определения
структуры электромагнитного поля волн
диэлектрического волновода необходимо
решить систему уравнений Максвелла:
,
, (2.1)
где
и
,
–
абсолютная диэлектрическая и магнитная
проницаемость
с
граничными условиями на поверхностях
раздела x=0,
x=t
и физическим условием убывания поля
при
.
Каждое из уравнений (2.1) равносильно трем скалярным уравнениям:
;
(2.2)
;
(2.3)
В
соответствии с методом комплексных
амплитуд
,
где
–
комплексная амплитуда. После сокращения
в (2.2), (2.3) на
получим уравнения для комплексных
амплитуд.
Задание: из уравнений Максвелла получить (2.5), (2.6).
Поскольку
в направляющих линиях необходимо
передавать энергию из одного сечения
в другое в виде бегущих в направлении
оси
OZ
волн, которые характеризуются множителем
бегущей волны
,
то аналогично случаю полых металлических
волноводов решение (2.2), (2.3) для комплексных
амплитуд
ищем в виде:
, (2.4)
где
-
комплексные амплитуды, зависящие только
от x
Г,1/м – коэффициент распространения
волны в рассматриваемой структуре.
После подстановки (2.4) в (2.2), (2.3) последние разделяется на две следующие независимые подсистемы:
(2.5)
(2.6)
Из
(2.5), (2.6) следует, что для рассматриваемого
случая моды делятся на волны типа H:
,
определяемые уравнением (2.5), для которых
отличны от нуля только составляющие
,
и на волны типа E:
,
определяемые уравнением (2.6), для которых
отличны от нуля только составляющие
.
Таким
образом, для определения структуры
возможных типов электромагнитных волн
волн в диэлектрическом пленочном
волноводе достаточно найти продольную
(вдоль оси OZ)
–
компоненту для H
-волн
или
-компоненту
для E
-волн,
поскольку поперечные компоненты затем
можно вычислить, используя (2.5), (2.6). Из
уравнений (2.5), (2.6) видно, что для определения
структуры электромагнитных волн в
диэлектрическом волноводе удобно
использовать компоненты
–
компоненту для H–волн
и
–компоненту
для E
-волн.
Задание: пояснить последнее утверждение.
Известно, что каждая из компонент электромагнитного поля в каждой из областей на рис.1.2,б удовлетворяет однородному волновому уравнению
(2.7)
с
соответствующими граничными условиями
на поверхностях разделов
и условию убывания при
;
полагалось, что
В (2.7)
– волновое число свободного пространства
(
–
длина волны);
– оператор Лапласа;
–
относительная диэлектрическая
проницаемость сред.