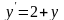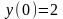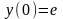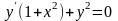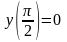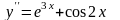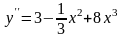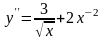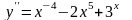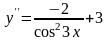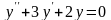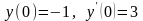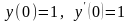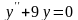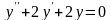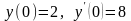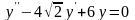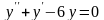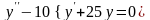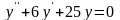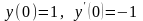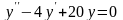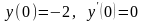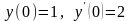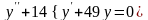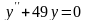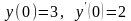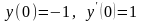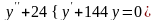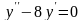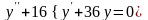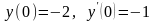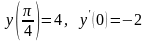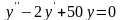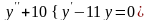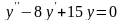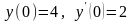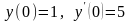2.8.3.3. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Рассматриваемые уравнения имеют вид:

где p и q – некоторые действительные числа.

Для того чтобы решить данное дифференциальное уравнение, нужно составить так называемое характеристическое уравнение:

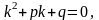
По какому принципу составлено характеристическое уравнение, отчётливо видно:

вместо второй производной записываем k²;

вместо первой производной записываем k

вместо функции y ничего не записываем.

– это обычное квадратное уравнение, которое предстоит решить.

В зависимости от корней этого уравнения исходное дифференциальное уравнение имеет разные виды общих решений.

Если характеристическое уравнение имеет два различных действительных корня k₁≠k₂, (т.е., если дискриминант D>0), то общее решение однородного уравнения выглядит так:

Если характеристическое уравнение имеет два совпадающих действительных корня k₁=k₂=k, (т.е., если дискриминант D=0), то общее решение однородного уравнения выглядит так:

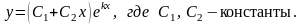
Если характеристическое уравнение имеет два сопряженные комплексные корни k₁=+i, k₂=-i (т.е., если дискриминант D<0), то общее решение однородного уравнения выглядит так:

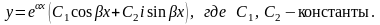
Если получаются чисто мнимые сопряженные комплексные корни: k_1,2=±i , то общее решение упрощается:

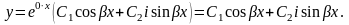
Примеры.

а) Решить дифференциальное уравнение

Решение.

Составим и решим характеристическое уравнение

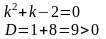
Характеристическое уравнение имеет два различных действительных корня

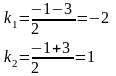
Общее решение имеет вид

Выполним проверку. Берем ответ и находим производную:

Находим вторую производную:

Подставляем найденные значения производных в левую часть исходного уравнения:

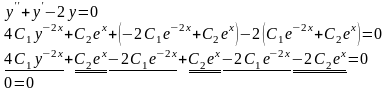
Получено тождество, значит, общее решение найдено правильно.

b) Решить дифференциальное уравнение

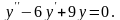
Решение.

Составим и решим характеристическое уравнение:

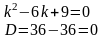
Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно применить известную формулу сокращенного умножения:

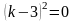
Получены два кратных действительных корня k_1,2=3

Общее решение имеет вид:

с) Решить однородное дифференциальное уравнение второго порядка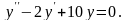

Решение.

Составим и решим характеристическое уравнение:

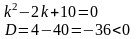
Характеристическое уравнение имеет сопряженные комплексные корни:

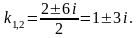
Общее решение имеет вид:

d) Найти частное решение дифференциального уравнения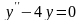 , удовлетворяющее начальным условиям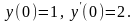

Решение.

1.Cоставим и решим характеристическое уравнение:

Получены два различных действительных корня, поэтому общее решение:

2.Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие :

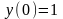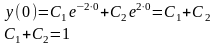
Далее берём наше общее решение и находим производную:

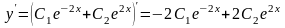
Используем второе начальное условие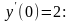

Составим и решим систему из двух найденных уравнений:

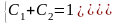
Подставляем найденные значения констант в общее решение:

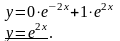
Получено частное решение.

Проверка осуществляется по следующей схеме:

Сначала проверим, выполняется ли начальное условие :

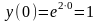– начальное условие выполнено.

Находим первую производную от ответа:

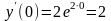– второе начальное условие тоже выполнено.

Находим вторую производную:

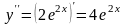
Подставим 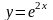и в левую часть исходного дифференциального уравнения :

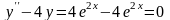что и требовалось проверить.

Таким образом, частное решение найдено, верно.

Задания для практической работы №5.

Задача 1. Найти частное решение дифференциального уравнения, удовлетворяющего условию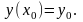

Вариант	Дифференциальное уравнение	Начальное условие
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Задача 2. Найти общее решение дифференциального уравнения.

Вариант	Дифференциальное уравнение	Вариант	Дифференциальное уравнение
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Задача 3. Найти общее решение дифференциального уравнения.

Вариант	Дифференциальное уравнение	Вариант	Дифференциальное уравнение
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Задача 4. Найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.

Вариант	Дифференциальное уравнение	Начальные условия
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Срок сдачи практической работы

ОП-253	04.04.2014
ОП-254	02.04.2014

Полякова И.А. Лекции по математике. Технический профиль. 2 курс.