4.5. Гексагональная симметрия

4.5.1. Простые гексагональные решетки

Простыми решетками с гексагональной симметрией являются так называемые гесагональные структуры с плотной упаковкой (г.п.у.). чтобы построить структуру с плотной упаковкой, начнем с плотноупакованного плоского слоя α, используя сферы диаметра а (рис. 4.14). далее на этом слое размещается другой плоский слой, причем плотная упаковка может осуществляться в двух вариантах: β и γ. Расстояние между плоскостями α-γ и α-β равны 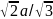. Любая последовательность таких слоев представляет собой плотную упаковку. Периодическая последовательность …αβ γ αβ γ… представляет собой кубическую гранецентрированную решетку; при этом построенные плоскости являются плоскостями (111). Гексагональные решетки с плотной упаковкой соответствуют периодической последовательности …αβ γ αβ γ…; они не являются решетками Бравэ (базисные векторы и элементарная решетка представлены на рис. 4.14). в элементарной ячейке, построенной на атомах в положении α, содержится также еще один атом в положении β. Параметры решетки определяются величинами а и Для идеальной упаковки с/а=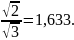 В общем случае межплоскостное расстояние не соответствует идеальному, но мало отличается от 1,633 (см. табл. 4.4). Направление а⁽³⁾ называется гексагональной осью, а плоскости перпендикулярные ей, называются базисными плоскостями.

В то время как плотноупакованный плоский слой имеет ось симметрии 6-го порядка (параллельную а⁽³⁾), ГПУ-решетка не имеет такой симметрии, поскольку поворот на угол 2π/6 вокруг атома α переводит α в α, но β в γ. Однако инверсия также переводит β в γ; поэтому поворот на угол 2π/6 вместе с инверсией является преобразованием симметрии для ГПУ-решетки. Поскольку инверсия не меняет С (как тензор 4-го ранга), тензор С также инвариантен по отношению к поворотам на угол 2π/6 относительно оси а⁽³⁾. Это означает изотропию С относительно а⁽³⁾. Остальные преобразования симметрии соответствуют поворотам относительно центра призмы с сечением в виде правильного шестиугольника, и вид тензора С, удовлетворяющего такой симметрии. Можно легко получить.

4.5.2. Параметры теории упругости металлов с гексагональной симметрией

В случае гексагональной симметрии параметры теории упругости включают пять независимых величин; в представлении Фойгта имеем

С = 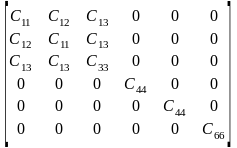= 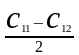(4.48)

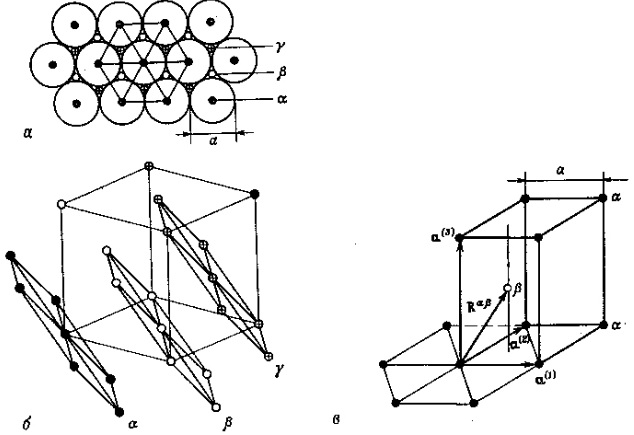
Рис. 4.14. Гексагональные решетки с плотной упаковкой. а- плотноупакованный плоский слой, построенный из сфер диаметра а: позиции α (черные кружки); позиции β и γ вне плоскости (обозначены кружками с крестом); б- последовательность αβ γ αβ γ… образует ГЦК-решетку; в- последовательность αβαβ… образует гексагональную решетку с плотной упаковкой. Базисными векторами являются а⁽¹⁾ = а(1,0,0), а⁽²⁾ = а/2(1,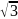 ,0), а⁽³⁾ = 2 а/ (0,0,1); в элементарной ячейке – 2 атома: один в позиции α R^α = 0 и другой – в позиции β R^αβ = (а⁽¹⁾ + а⁽²⁾)/3 + а⁽³⁾/2.

Таблица 4.4 Модули упругости [10¹² дин/см²], постоянные решетки а [Ǻ] и с [Ǻ] и плотность ρ₀ [г/см³] для металлов с ГПУ-решеткой; ссылки (б) и (в) см. в табл. 4.2.

Металл	ρ0	а	с	с11	с12	с13	c33	с44	Ссылка
Be	1,85	2,29	3,58	2,92	0,267	0,140	3,36	1,63	В
Ce	8,64	2,98	5,62	1,15	0,395	0,399	0,509	0,199	В
Co	8,84	2,51	4,07	3,07	1,65	1,03	3,58	0,755	Б
Hf	12,7	3,19	5,05	1,81	0,772	0,661	1,97	0,557	Б
Mg	1,74	3,21	5,21	0,597	0,262	0,217	0,617	0,164	Б
Re	21,0	2,76	4,46	6,13	2,70	2,06	6,83	1,63	Б
Ru	12,4	2,71	2,28	5,63	1,88	1,68	6,24	1,81	В
Ti	4,51	2,95	4,68	1,62	0,920	0,690	1,81	0,467	Б
Tl	11,6	3,46	5,53	0,408	0,354	0,29	0,528	0,073	Б
Y	4,47	3,65	5,73	0,779	0,285	0,21	0,769	0,243	Б
Zn	7,14	2,66	4,95	1,64	0,364	0,530	0,635	0,388	Б
α-Zr	6,51	3,23	5,15	1,43	0,728	0,653	1,65	0,320	Б

В табл. 4.4 приведены параметры многих металлов с гексагональной симметрией. Тензор s_αβ следует такой же схеме. Для четырех модулей сдвига, связанных с собственными тензорами Т(2, 4, 5, 6), получаем как и в случае кубической симметрии,

; (4.48a)

Для других компонент s_αβ следует вычислить обратную матрицу по отношению к матрице 3х3 в верхней левой части (4.48). В результате имеем:

(4.48б)