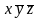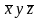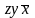- •4.4 Кубическая симметрия
- •4.4.1 Тензор упругих модулей с
- •4.4.2 Собственные тензоры
- •4.4.3. Уравнения движения
- •4.4.4. Обзор параметров теории упругости
- •4.5. Гексагональная симметрия
- •4.5.1. Простые гексагональные решетки
- •4.5.2. Параметры теории упругости металлов с гексагональной симметрией
- •4.5.3. Собственные состояния тензора с
4.4 Кубическая симметрия
4.4.1 Тензор упругих модулей с
В СЛУЧАЕ КУБИЧЕСКОЙ СИММЕТРИИ
Если, исходя из соотношений
σ = С ε, σik = Сik, mn εmn или σμ = (T(μ), CT(ν))εν = Cμνεν,
подвергнуть кристалл операции поворота, то соотношение между σ и ε изменится, коль скоро поворот не является операцией симметрии, переводящий тензор С самого в себя. Если обозначить знаком «тильда» любой из 48 поворотов D, соответствующих кубической симметрии (поскольку тензор четного ранга инвариантен по отношению к инверсии, достаточно рассмотреть 24 собственных поворота), для преобразованного тензора Č имеем
Č = С, Čik, mn = Diiʹ Dkkʹ Dmmʹ Dnnʹ Ciʹ kʹ mʹ nʹ , (4.36)
(T(μ), ČT(ν)) = (T/(μ), CT(ν)) или также (Ť(μ), CŤ(ν)) = (T(μ), CT(ν)).
Если учесть все ограничения (4.26), что не составляет труда1), приходим к следующим соотношениям:
Сik, mn = С12δikδmn + C44 (δimδkn + δinδkm) + (C11 - C12 – 2C44) δikmn, (4.37)
С = С12А1 + С44А2 + (C11 - C12 – 2C44)А3,
где C11 - C12 – 2C44 = Са, δikmn = 1, если все индексы одинаковы и δikmn = 0в иных случаях. В представлении Фойгта
Сαβ
=

 (4.37а)
(4.37а)
Два первых члена А2,2 в (4.37) изотропны (инвариантны относительно любых поворотов), а третий член А3, соответствует кубической симметрии (инвариантен по отношению к поворотам, отвечающим кубической симметрии). Если
Са = C11 - C12 – 2C44 = 0 – условие изотропности
(Са –мера анизотропии), (4.38)
то кристалл изотропен3.Кубические кристаллы имеют 3 независимых параметра теории упругости, а изотропные кристаллы – 2. В силу требования упругой устойчивости собственные значения матрицы (4.37а) должны быть положительны,
C11 + 2C12 >0, 1 x; C11 - C12 > 0, 2 x; C44 > 0, 3 x (4.39)
4.4.2 Собственные тензоры
И СОБСТВЕННЫЕ ЗНАЧЕНИЯ
Схема Фойгта не очень наглядна; в частности, величины Сαβ пока не имеют непосредственного физического смысла. Наиболее удобным и наглядным для наших целей является базис T(ν) (4.12 – 4.14), поскольку он связан с кубической симметрией, а матрица Cμν оказывается диагональной
Cμν
=
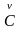 δμν,
Σ;
δμν,
Σ;
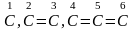 ;
;
С = T(ν)
Cνμ
T(μ)
=
 СТ(μ)
=
СТ(μ)
=
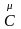 Т(β),
Σ (4.40)
Т(β),
Σ (4.40)
Это можно легко усмотреть из поведения состояний T(ν) при кубических поворотах, некоторые из которых описаны в табл. 4.1. Эти результаты можно получить, обратившись к рис. 4.5. Первый столбец показывает, что состояния 1, 2, 2ʹ, 2ʹʹ, 3, 4 – собственные состояния оператора поворота на угол π вокруг оси [100]с собственным значением 1, а состояния 5, 6 соответствуют собственным значениям (-1), поэтому
С15 = (Т(1), СТ(5)) = (Ť(1), СŤ(5)) = -(Т(1), СТ(5)) = -С15 = 0.
Из анализа табл. 4.1 можно усмотреть, что тензор Cμν диагонале4. Из 2-го столбца следует, что Ť(6) = Т(5) и поэтому
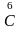 =
С66 =
(Т(6), СТ(6)) = (Ť(6), СŤ(6)) = С55
=
=
С66 =
(Т(6), СТ(6)) = (Ť(6), СŤ(6)) = С55
=
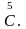
Аналогично,
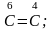 далее
С22 =
С2ʹ 2ʹ =
С2ʹʹ 2ʹʹ,
С22ʹ =
С2ʹ 2ʹʹ
= С2ʹʹ 2.
далее
С22 =
С2ʹ 2ʹ =
С2ʹʹ 2ʹʹ,
С22ʹ =
С2ʹ 2ʹʹ
= С2ʹʹ 2.
То, что
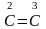 ,
можно также усмотреть из соотношения
,
можно также усмотреть из соотношения
С33 = (С2ʹʹ 2ʹʹ + С2ʹ 2ʹ - С2ʹʹ 2ʹ - С2ʹ 2ʹʹ)/3 = (2С22 - С22ʹ - С22ʹʹ)/3 = С22,
если учесть исходя из равенства Т(2ʹ ) + Т(2ʹʹ ) = -Т(2), что С22ʹ + С22ʹʹ = С2, 2ʹ + 2ʹʹ = -С22.
Тогда из (4.40) явствует, что T(ν) – собственные состояния (тензоры 2-го ранга) тензора 4-го ранга С, соответствующие собственным значениям , и, конечно, удобнее всего выразить С через собственные состояния и собственные значения. Соотношения (4.40), кроме того, указывает, что сдвиговые деформации и сдвиговые напряжения, а также растяжение и давление непосредственно связаны друг с другом:
σμ = εμ, Σ. (4.40а)
Очевидно, в случае
кубической симметрии тензор С имеет 3
независимых модуля, т.е. 3 независимых
собственных значения
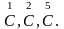
В изотропном случае
С описывают 2 независимых модуля, так
что
 поскольку связь между сдвиговыми
напряжениями и деформациями не может
зависеть от конкретного вида сдвига.
Тензор упругих податливостей принимает
вид
поскольку связь между сдвиговыми
напряжениями и деформациями не может
зависеть от конкретного вида сдвига.
Тензор упругих податливостей принимает
вид
S
=
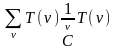 ,
(4.40б)
,
(4.40б)
Таблица 4.1. Преобразования базисных тензоров T(ν) при операциях кубической симметрии
Ось |
[100]
|
[010] |
[001]
|
||||
Угол поворота |
π |
π/2 |
π |
π/2 |
π |
π/2 |
|
Преобразование (xyz)
|
|
|
|
|
|
|
|
T(ν) переходит в ν = |
1 |
T(1) |
T(1) |
T(1) |
T(1) |
T(1) |
T(1) |
2 |
T(2) |
-T(2ʹʹ) |
T(2) |
-T(2ʹ) |
T(2) |
-T(2) |
|
2ʹ |
T(2ʹ) |
- T(2ʹ) |
T(2ʹ) |
- T(2) |
T(2ʹ) |
- T(2ʹʹ) |
|
2ʹʹ |
T(2ʹʹ) |
- T(2) |
T(2ʹʹ) |
- T(2ʹʹ) |
T(2ʹʹ) |
-T(2ʹ) |
|
3 |
T(3) |
--- |
T(3) |
--- |
T(3) |
T(3) |
|
4 |
T(4) |
-T(4) |
-T(4) |
T(6) |
-T(4) |
-T(5) |
|
5 |
-T(5) |
-T(6) |
T(5) |
-T(5) |
-T(5) |
T(4) |
|
6 |
-T(6) |
T(5) |
-T(6) |
-T(4) |
T(6) |
-T(6) |
и условие упругой устойчивости просто означает, что
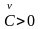 ,
ср. (4.39), (4.41)
,
ср. (4.39), (4.41)
поскольку (ε, Сε)
=
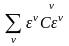 .
.
Физический смысл
величин
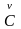 ясен из соотношения (4.40а) и демонстрируется
на рис. 4.10. Картина, соответствующая
тензору Т(1), приведена на рис. 4.10а; картины
напряжений и деформаций одинаковы, они
различаются лишь множителем
ясен из соотношения (4.40а) и демонстрируется
на рис. 4.10. Картина, соответствующая
тензору Т(1), приведена на рис. 4.10а; картины
напряжений и деформаций одинаковы, они
различаются лишь множителем
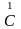 .
Соответственно имеем
.
Соответственно имеем
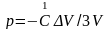 или
или
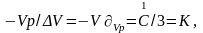
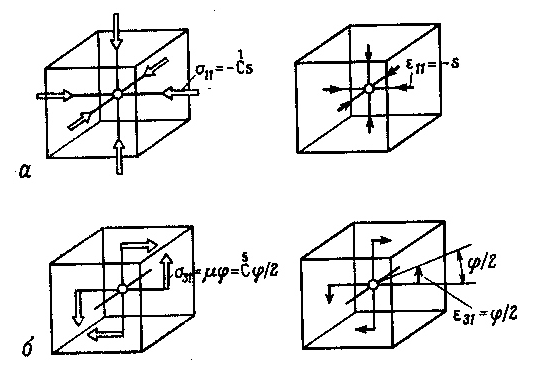
Рис.4.10. Физический смысл собственных значений С. а – картина, соответствующая тензору Т(1),
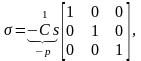
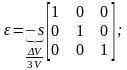
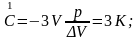
б – картина сдвига Т(5)

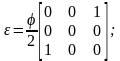
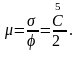
Где К называется
модулем всестороннего сжатия, или
объемным модулем. На рис. 4.10, б приведена
картина сдвига Т(5). Отношение сдвигового
напряжения и угла сдвига, в данном случае
равное
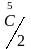 называется модулем сдвига µ для сдвигов
(100). Для сдвигов (110) ситуация аналогичная,
причем соответствующий модуль
называется модулем сдвига µ для сдвигов
(100). Для сдвигов (110) ситуация аналогичная,
причем соответствующий модуль
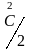 обозначается
через µ´. Связь между модулями Фойгта
Сαβ
и собственными значениями
обозначается
через µ´. Связь между модулями Фойгта
Сαβ
и собственными значениями
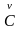 дается
соотношениями
дается
соотношениями
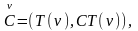
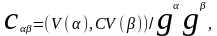 (4.42)
(4.42)
и (4.12-4.14), которые выражают тензоры Т(ν) через тензоры V(α).
В конечном счете
 K
– модуль всестороннего
сжатия, (4.43а)
K
– модуль всестороннего
сжатия, (4.43а)
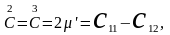 µ´
- модуль сдвига для сдвигов (110) (4.43б)
µ´
- модуль сдвига для сдвигов (110) (4.43б)
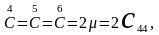 µ
- модуль сдвига для сдвигов (110) (4.43в)
µ
- модуль сдвига для сдвигов (110) (4.43в)
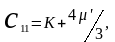

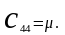 (4.43г)
(4.43г)
Если ввести операторы проектрирования pk, pµ´, pµ на состояния Т(1), Т(2) и Т(3), Т(4) и Т(5) и Т(6), где pk отбирает растяжения, а pµ´, pµ - соответствующие сдвиги, можно написать

Сравнивая с (4.37) (С = с12А1 + с44А2 + (с11 - с12 - 2с44)А3), получаем соотношения
А1=3pk; A2=2; A3=1 - pµ .
Следовательно,
С=(с11 + 2с12)pk + (c11-c12)pµ´+2c44pµ,

что устанавливает связь между sαβ и сαβ.
Смысл описанного
выше представления С весьма прозрачен;
оно более наглядно, чем представление
Фойгта, и мы будем пользоваться им далее
при анализе кубических кристаллов.
Полезным применением этого нового
представления является вычисление так
называемых средних Фойгта. Оно состоит
в усреднении С по всем ориентациям
кристалла; получающийся в результате
тензор
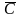 изотропен.
Считается, что он приближенно описывает
упругие модули поликристаллов, которые
изотропны. Для кубических кристаллов
это среднее можно без труда вычислить
исходя из (4.44а). поскольку величина pk
инвариантна
изотропен.
Считается, что он приближенно описывает
упругие модули поликристаллов, которые
изотропны. Для кубических кристаллов
это среднее можно без труда вычислить
исходя из (4.44а). поскольку величина pk
инвариантна
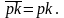 Далее ясно, что для сдвиговых компонент
величина
Далее ясно, что для сдвиговых компонент
величина
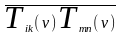 не
должна зависеть от ν и равна (1-pk)/5,
где (1-pk)=
ps отбирает
все сдвиги. Поэтому
не
должна зависеть от ν и равна (1-pk)/5,
где (1-pk)=
ps отбирает
все сдвиги. Поэтому
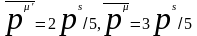
И
 где
(4.45)
где
(4.45)
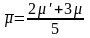 (4.45а)
(4.45а)
представляет собой
среднее взвешенное от двух кубических
модулей сдвига; веса 2 и 3 соответствует
размерностям пространств сдвигов pµ´,
pµ.
Легко показать, что значения К для
монокристаллов и поликристаллов равны.
Но среднее Фойгта
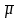 дает
только приближенное значение для модуля
сдвига изотропного поликристалла µэфф.
В действительности
есть
верхний предел для этой величины. Нижний
же предел устанавливается так называемыми
средними Рейсса, равными
дает
только приближенное значение для модуля
сдвига изотропного поликристалла µэфф.
В действительности
есть
верхний предел для этой величины. Нижний
же предел устанавливается так называемыми
средними Рейсса, равными
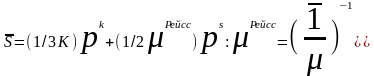
Более подробно эти предельные значения будут рассматриваться в разд. 4.8.7.

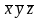 (
(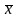 = -x)
= -x)