
- •Математическая статистика
- •1. Статистическая модель и задачи математической статистики
- •2. Способы представления статистических данных.
- •3. Эмпирическая функция распределения и ее свойства.
- •4. Гистограмма и полигон частот.
- •5. Выборочные (эмпирические) числовые характеристики
- •6. Оценивание неизвестных параметров распределений
- •6.1. Точечные оценки неизвестных параметров распределений и требования, предъявляемые к ним
- •Несмещенность
- •Состоятельность
- •6.2. Свойства выборочного среднего и выборочной дисперсии
- •6.3. Методы нахождения точечных оценок
- •6.3.1. Метод моментов
- •6.3.2. Метод максимального правдоподобия
6.3. Методы нахождения точечных оценок
Наиболее распространенными методами получения точечных оценок неизвестных параметров распределений, удовлетворяющих требованиям 1) – 3) (хотя бы частично), являются метод моментов и метод максимального правдоподобия.
6.3.1. Метод моментов
Метод моментов, предложенный К. Пирсоном, является исторически первым общим методом точечного оценивания неизвестных параметров распределений. Суть его состоит в следующем.
Пусть
- выборка из генеральной совокупности,
имеющей функцию распределения
,
зависящую от векторного параметра
![]() (задана параметрическая модель
наблюдений).
(задана параметрическая модель
наблюдений).
Предположим,
что у наблюдаемой случайной величины
существуют первые
![]() моментов
моментов
![]() .
Они являются функциями от неизвестного
параметра
:
.
Они являются функциями от неизвестного
параметра
:
![]() .
.
Рассмотрим
выборочные начальные моменты
 ,
рассчитанные по данной выборке
(это числа!).
,
рассчитанные по данной выборке
(это числа!).
Метод моментов состоит в приравнивании теоретических моментов соответствующим выборочным моментам. При этом получается система уравнений
![]()
с
неизвестными
![]() .
.
Если
данная система уравнений имеет
единственное решение, то оно называется
оценкой параметра
,
полученной по методу моментов и
обозначается
![]() .
.
Для нахождения оценки может быть использована также система уравнений, основанных на приравнивании центральных теоретических соответствующим центральным выборочным моментам:
![]()
или смешанная система уравнений, часть из которых основана на приравнивании начальных теоретических и выборочных моментов, а часть – на приравнивании теоретических и выборочных центральных моментов. Использование именно первых r моментов также не является обязательным. Получаемые во всех этих случаях оценки, вообще говоря, отличаются друг от друга. Но при больших объемах выборки отличия этих оценок незначительны, и все они, по-прежнему, называются оценками, полученными по методу моментов.
В
случае двумерного неизвестного параметра
![]() его оценка по методу моментов
его оценка по методу моментов
![]() обычно определяется как решение системы
уравнений:
обычно определяется как решение системы
уравнений:
 .
.
Оценки, полученные по методу моментов являются:
- состоятельными (при весьма общих предположениях);
- несмещенными не всегда;
- вообще говоря, неэффективными.
На практике оценки, полученные по методу моментов, часто используются как первое приближение, на основе которого находятся более «хорошие» оценки.
Достоинство метода моментов заключается в том, что системы уравнений для нахождения оценок решаются довольно просто. Однако имеет место произвол в выборе уравнений для нахождения оценок и метод вообще неприменим, когда моментов необходимого порядка не существует (например, в случае закона распределения Коши).
Пример
1.
Наблюдаемая случайная величина
имеет показательное (экспоненциальное)
распределение
![]() с
неизвестным параметром
,
то есть имеет плотность вероятностей
вида:
с
неизвестным параметром
,
то есть имеет плотность вероятностей
вида:
![]() .
Требуется по выборке
найти оценку параметра
по методу моментов.
.
Требуется по выборке
найти оценку параметра
по методу моментов.
Решение.
Для показательного закона распределения известно, что
 ,
,
 ,
,
 .
.
На основании этого можно получить три различные оценки параметра по методу моментов.
а)
Используя уравнение
![]() ,
имеем
,
имеем
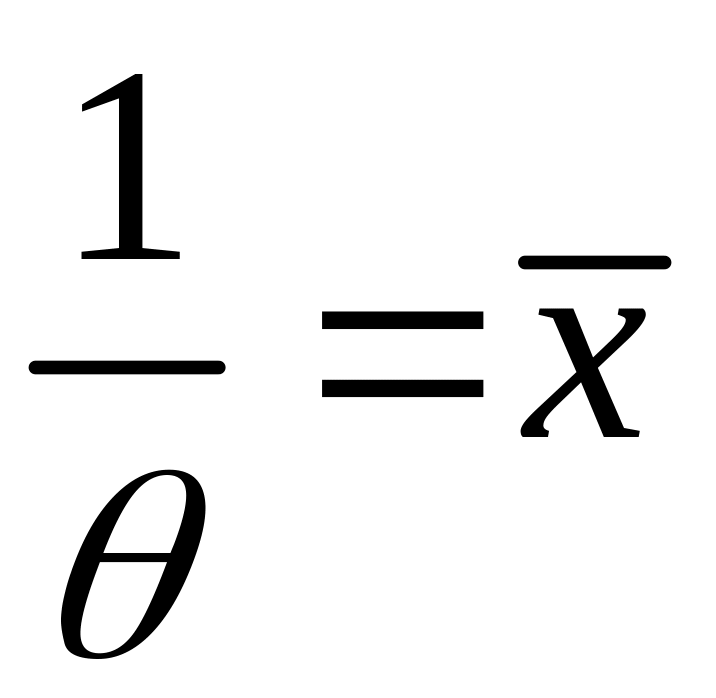 .
Следовательно,
.
Следовательно,
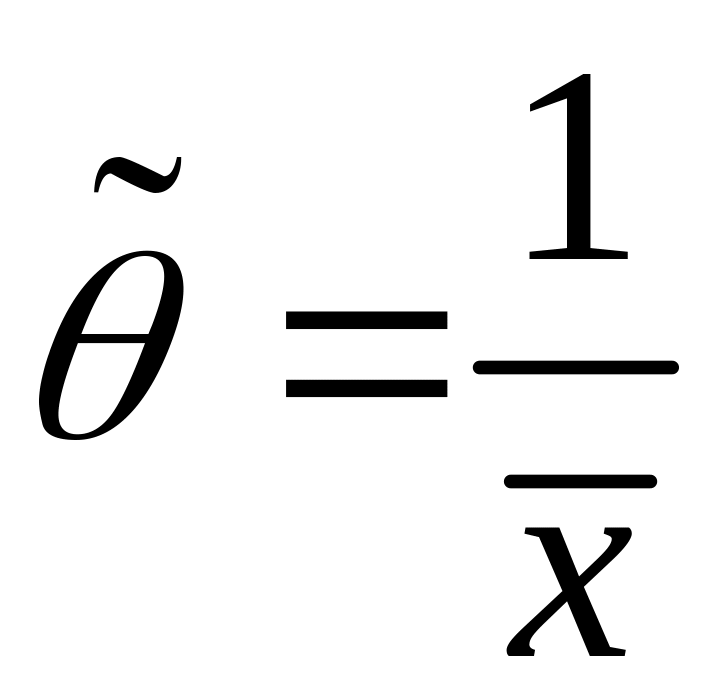 .
.
б)
Используя уравнение
![]() ,
имеем
,
имеем
 .
Следовательно,
.
Следовательно,
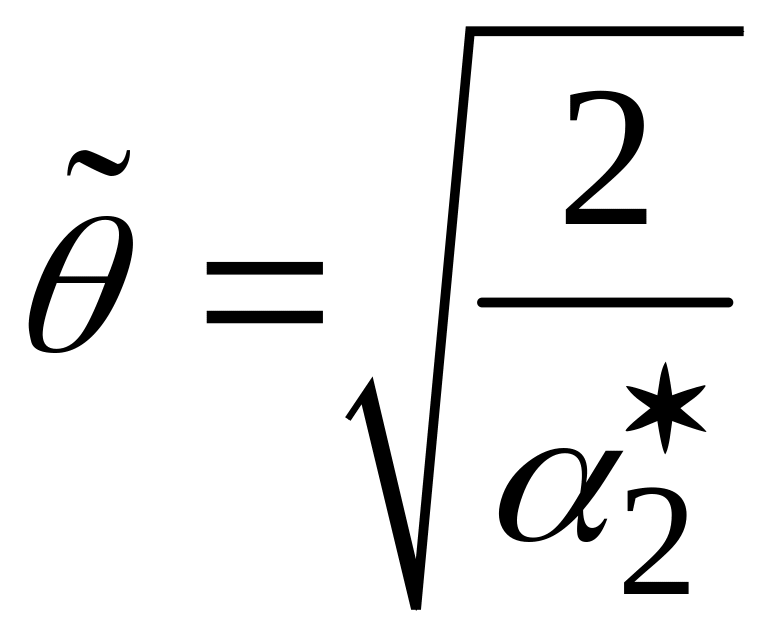 .
.
в)
Используя уравнение
![]() ,
имеем
,
имеем
 .
Следовательно,
.
Следовательно,
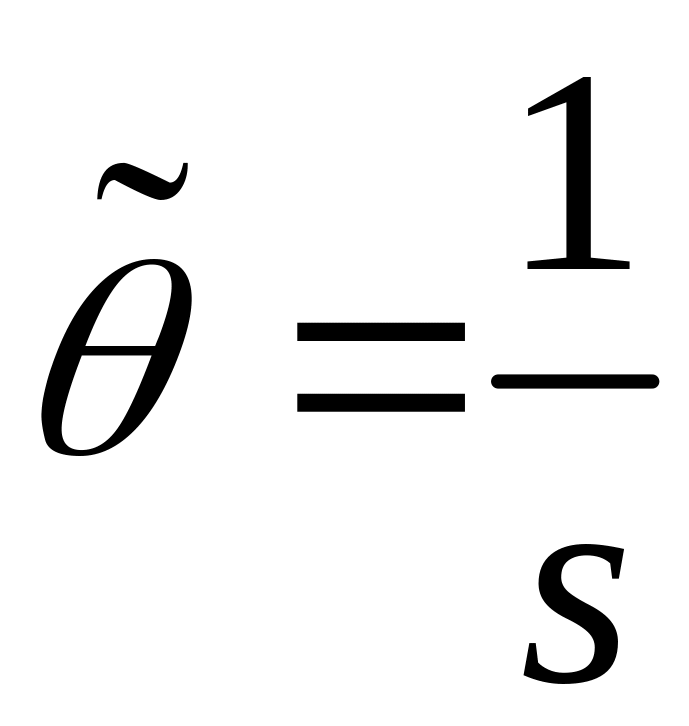 .
.
При больших эти три оценки параметра отличаются друг от друга незначительно.
Пример 2. Наблюдаемая случайная величина имеет закон распределения Пуассона с неизвестным параметром :
 .
.
Требуется по выборке найти оценку параметра по методу моментов.
Решение.
Известно,
что
![]() .
.
На основании этого можно получить две оценки параметра по методу моментов:
![]() ,
,
![]() .
.
При
больших
эти оценки отличаются незначительно.
Приближенное равенство
![]() является характерной особенностью
закона распределения Пуассона.
является характерной особенностью
закона распределения Пуассона.
